
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазовый синхронизм в одноосных кристаллахСодержание книги
Поиск на нашем сайте
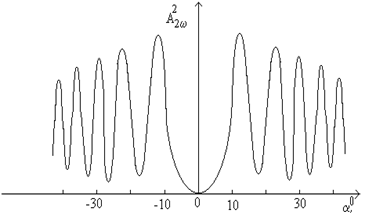
Итак, согласно предыдущему параграфу, используя нелинейные среды в принципе можно преобразовать частоту исходной световой волны. Известно, что в среде с дисперсией показателя преломления световые волны различной частоты имеют различные скорости распространения. Если в кристалле распространяется плоская волна с частотой ω E1 = E10cos(ωt –k1z), (7.12) и ее вторая гармоника с частотой 2ω: E2 = E20cos(2ωt –k2z), (7.13) то соответствующие этим волнам фазовые скорости равны: u1=с/nw=w /k1 и u2=с/n2w=2w /k2. (7.14) Вследствие дисперсии показателя преломления в среде nw≠n2w, и, следовательно, u1 ≠u2. Из неравенства фазовых скоростей с учетом (7.15) получаем k1≠k2, или, 2 k1-k2=Δk (7.15) Эта разность волновых чисел Δk носит название волновой расстройки. Амплитуда волны второй гармоники в точке z, генерируемой в среде с дисперсией, дается выражением: A2w(z)=(2A/Δk)sin(Δkz/2), (7.16) и она достигает своего первого максимума на расстоянии, называемой длиной когерентности: lког=p/Δk=l/4(nw -n2w), (7.17) где l=(2pс/w) -длина волны основной волны в вакууме. Выбрав, например, l»1мкм и Dn»10-2, получим lког»25мкм. Экспериментальная зависимость интенсивности второй гармоники в кристалле кварца от угла поворота пластинки показана на рис.7.3.
Как видим из этого рисунка, после достижения максимального значения интенсивность второй гармоники начинает уменьшаться. Если z>>lког, то амплитуда волны второй гармоники имеет характер биений согласно выражению (7.16). Однако повышение эффективности преобразования во второй гармонике возможно при выполнении так называемого условия фазового синхронизма, если выполняется условие: Δk=0, или k2=2k1. (7.18) Условие (7.18) называется условием волнового или фазового синхронизма, и оно эквивалентно условию равенства фазовых скоростей волны второй гармоники и исходной волны. Выполнить условие равенства фазовых скоростей для взаимодействующих волн удается в оптически анизотропных кристаллах с двулучепреломлением. Известно, что в одноосном кристалле могут распространяться две монохроматические волны ортогональных поляризаций (обыкновенная и необыкновенная) с одинаковыми частотами, но с разными фазовыми скоростями, т.е. с разными показателями преломления. Рассмотрим сечение индикатрисы показателя преломления отрицательного одноосного кристалла (no>ne) для волны основной частоты w и ее второй гармоники частоты 2w.
Как видно из рисунка 7.4., в направлениях ОА, образующих угол qc с оптической осью Z, выполняется равенство показателей преломления обыкновенной волны на частоте w и необыкновенной волны на частоте 2w т.е.: nwо=n2we. (7.19)
Равенство (7.19) является условием фазового синхронизма для генерации второй гармоники. Для выполнения синхронизма волновые векторы должны быть ориентированы по направлению ОА. Эти направления называются направлениями синхронизма, а угол qс - углом синхронизма. Показатель преломления для необыкновенной волны можно изменять, меняя угол между волновой нормалью и оптической осью и вычислить из выражения ne(q)=nenо/[nо2-(nо2-ne2)cos2q]1/2, (7.20) где n0 и ne - главные значения показателя преломления на частоте w. Используя выражение (7.20) можно легко вычислить угол синхронного взаимодействия волн в нелинейном кристалле.
Самофокусировка света
Физические причины этого нелинейного эффекта заключаются в изменении показателя преломления среды в сильном световом поле. Первый член в формуле (7.11) обладает периодичностью во времени такой же, как и у первичной волны. Однако это – нелинейный член, так как в качестве коэффициента при cos(wt-kх) стоит qE03. Таким образом, с кубичным по полю членом в нелинейной поляризации связано переизлучение на частоте падающей волны, но с амплитудой, пропорциональной коэффициенту q и кубу амплитуды падающей волны. Этот член обусловливает появление нелинейной поправки к показателю преломления среды. Электрическая индукция D на частоте w может быть представлена в виде: D=e0eE=e0eЕ0 cos(wt - kх)=[1+c+3/4qE02]e0Е0сos(wt-kх) (7.21) и, следовательно, диэлектрическая проницаемость: e =n2=eл + e2Е02 (7.22) где eл=1+c, а e2=3/4q. Поскольку e2Е02<<eл, то (7.22) можно переписать в виде: n= n0 +n2E2 (7.23) где n0=eл1/2. Таким образом, интенсивная световая волна изменяет показатель преломления среды. Добавочный член n2E2 тем больше, чем больше интенсивность падающей волны. Такие оптические эффекты принято называть самовоздействием световой волны. За счет появления нелинейных добавок к диэлектрической проницаемости e (или к показателю преломления n) световая волна изменяет собственную фазовую скорость
В поле ограниченного интенсивного светового пучка первоначально однородная среда в силу формулы (7.23) становится оптически неоднородной, следовательно, показатель преломления среды определяется теперь распределением интенсивности распространяющейся волны. Это приводит к явлению нелинейного преломлению света, характер которого определяется знаком нелинейной добавки n2E2. В среде с n2>0 области максимальной интенсивности света являются одновременно и наиболее оптически плотными. В этом случае нелинейное преломление должно приводить к самофокусировке, так как периферийные лучи отклоняются в область, где поле максимально. Чрезвычайно важным обстоятельством, выделяющим эффект самофокусировки среди других нелинейных оптических процессов, является его «лавинный» характер. Действительно, даже слабое увеличение интенсивности в некотором участке светового пучка в среде с n2>0 приводит к концентрации лучей в этой области, следовательно, и к дополнительному возрастанию интенсивности, которое еще усиливает эффект нелинейного преломления и т.д. Однако пучок с конечным поперечным сечением должен одновременно дифрагировать. Если эффект самофокусировки окажется сильнее дифракции, только тогда пучок будет сфокусирован. Так как действие самофокусировки пропорционально n2E2, а действие дифракции обратно пропорционально квадрату радиуса пучка, следовательно, когда пучок сжимается из-за самофокусировки, одновременно усиливается действие и самофокусировки, и дифракции. Если последняя возрастает быстрее, то в некоторой точке дифракция берет верх над самофокусировкой и сфокусированный пучок, достигнув минимального сечения (фокальной точки) должен расходиться. Условия самофокусировки. Пусть в нелинейной среде с n2>0 распространяется цилиндрический пучок радиуса а (рис.7.5). Тогда вне пучка показатель преломления n0=eл1/2, а внутри пучка: n=n0+n2E2. Лучи, падающие на границу пучка изнутри, совершают переход из среды оптически более плотной в среду оптически менее плотную; следовательно, при достаточно больших углах a для них возможен эффект полного внутреннего отражения. Критический угол соответствует лучу, угол наклона β0 которого к оси пучка равен: β0=arccos[n0/(n0+n2E2)] (7.24)
Лучи с β>β0 отклоняются от оси пучка, лучи с β<β0 отклоняются к оси пучка. В пучке, фронт которого (поверхность равной фазы) на входе в нелинейную среду является плоским, угол β определяется дифракцией: βд=0,61λ0/n02a (7.25) Относительный вклад нелинейного преломления и дифракции в поведение такого пучка можно оценить, сравнивая углы β0 и βд. При β0<βд пучок расходится, однако темп дифракционной расходимости меньше, по сравнению с линейной средой. При β0=βд нелинейное преломление полностью компенсирует дифракционную расходимость луча; размеры и форма пучка остаются неизменными при распространении его в нелинейной среде. Пучок создаёт для себя своеобразный оптический волновод, по которому распространяется без расходимости. Этот режим называется режимом самоканализации волнового пучка. Пользуясь формулами (7.24) и (7.25), нетрудно убедиться, что условие (7.24) накладывает требование лишь на полную мощность пучка и величину нелинейности среды. Выражение для критической мощности самоканализирующегося пучка есть: βд2/2=n2E2кр/n0;
Pкр=λ20с(1,22)2/256n2. (7.26) При β0>βд и, следовательно, при P>Pкр лучи отклоняются к оси пучка –происходит самофокусировка (рис.7.6.). В этом случае нелинейная среда действует как собирающая линза. Её фокусное расстояние можно оценить, пользуясь формулой (7.26). Вводя дифракционную длину Rд=ka2/2 ≈ a/βд, получаем из (7.26), что условие β0=βд эквивалентно условию: Rд=a/2 Величина Rнл, имеющая размерность длины, называется эффективной длиной самофокусировки.
Рис.7.6. Самофокусировка интенсивного светового пучка
После самофокусировки луч превращается в тонкую нить на оси пучка. Для данной среды эта нить имеет постоянный диаметр в пределах ±20% и протяжённость равна нескольким сантиметрам. Диаметр нити равен диаметру фокального пятна, а интенсивность в нити – интенсивности в фокусе. Интенсивность света в такой нити может достигать десятков гигаватт на квадратный сантиметр.
Двухфотонное поглощение Одним из фундаментальных нелинейных эффектов, который имеет разнообразное практическое значение, является многофотонное поглощение, в частности двухфотонное поглощение, при котором одновременно поглощаются два фотона, вследствие чего электрон (в атоме, молекуле) переходит с основного уровня E1 на возбужденный уровень E2 (рис.7.7.б, в). При этом предполагается, что между начальным и конечным состояниями другие связанные электронные состояния отсутствуют.
Рис.7.7. Процессы поглощения фотона в веществе: а) однофотонное поглощение фотона с энергией ђω0; б) двухфотонное поглощение фотонов с энергией ђω1; в) двухфотонное поглощение фотонов с энергиями ђω2 и ђω3..
Поскольку двухфотонное поглощение является нелинейным процессом, сечение поглощения для него намного порядков меньше сечения однофотонного поглощения. Тем не менее, двухфотонное поглощение легко наблюдается при использовании лазеров.
Процесс в средах можно рассмотреть феноменологически, описывая относительные изменение интенсивности I плоских волн при их прохождении через двухфотонно поглощающую среду. Пусть два пучка распространяются вдоль оси z среды и испытывают ослабление из-за двухфотонного поглощения, которое описывается уравнениями:
где γ - коэффициент двухфотонного поглощения. Связанные уравнения (7.28) можно решить аналитически, если учесть, что: Это соотношение является следствием того, что в двухфотонном поглощении участвуют равные числа фотонов с частотами ω1 и ω2. Если I10 и I20 - интенсивности на входе в среду, то: Решение системы (7.28) можно получить, избавляясь от I1 или I2. Считая, что I10 > I20, находим:
если I10 >>I20, то ослаблением волны I1 можно пренебречь. В этом случае решение принимает вид: I1≈I10,, I2=I20exp(-Kz). (7.31) Интерес представляет частный случай, когда ω1=ω2 = ω. Тогда вместо (7.28) мы получим уравнение: решение, которого имеет вид: В случае слабого поглощения решение приводится к виду: Из уравнения (7.34) экспериментально, по методу пропускания можно определить величину коэффициента двухфотонного поглощения γ для среды. Как видно выражение (7.34) не содержит микроскопических параметров среды, и поэтому невозможно в рамках данного метода предсказывать значение коэффициента двухфотонного поглощения γ для интересующих нас сред, что является основным недостатком. Тем не менее, при рассмотрении многофотонных процессов методом теории возмущений, можно получить выражение для коэффициента двухфотонного поглощения в виде: где n2=ε11/2·ε21/2,
Как и ранее было отмечено, коэффициент двухфотонного поглощения γ прямо пропорционален мнимой части кубической нелинейной восприимчивости q, описывающей процесс двухфотонного поглощения.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.012 с.) |


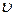 , а также коэффициент поглощения в среде, причем эти изменения пропорциональны квадрату амплитуды волны Е02. Это самовоздействие и приводит к эффекту самофокусировки света.
, а также коэффициент поглощения в среде, причем эти изменения пропорциональны квадрату амплитуды волны Е02. Это самовоздействие и приводит к эффекту самофокусировки света.
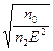 ≡Rнл. (7.27)
≡Rнл. (7.27)

 ,
,  , (7.28)
, (7.28)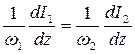 .
. (7.29)
(7.29) ,
, , (7.30)
, (7.30)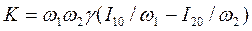
 , (7.32)
, (7.32) . (7.33)
. (7.33)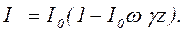 (7.34)
(7.34) ,
,  (7.35)
(7.35)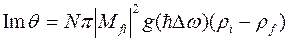 - мнимая часть кубической нелинейной восприимчивости q, N –плотность молекул или элементарные ячейки в среде, Mfi –матричные элементы двухфотонных переходов под действием световых волн с частотами w1 и w2 (рис.7.7), ri и rf - населенности состояний i и f.
- мнимая часть кубической нелинейной восприимчивости q, N –плотность молекул или элементарные ячейки в среде, Mfi –матричные элементы двухфотонных переходов под действием световых волн с частотами w1 и w2 (рис.7.7), ri и rf - населенности состояний i и f.



