
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ОСновы квантовых и оптоэлектронных приборовСодержание книги
Поиск на нашем сайте
А.Г. Акманов, Б.Г. Шакиров
ОСновы квантовых и оптоэлектронных приборов
Рекомендовано УМО по образованию в области телекоммуникации в качестве учебного пособия
Уфа 2003 УДК 621.378.1+621.383.4 ББК 32.86 А40
Рецензенты
кафедра «Телекоммуникационные системы» УГАТУ Маликов Р.Ф., доктор физико-математических наук, профессор БГПУ
Протокол №24 от 24.06.2003г. пленума Совета УМО по образованию в области телекоммуникации.
Акманов А.Г., Шакиров Б.Г.
А40 Основы квантовых и оптоэлектронных приборов. Учебное пособие. Уфа: РИО БашГУ, 2003. - 129 с. ISBN
Данная работа является учебным пособием по дисциплинам «Оптоэлектронные и квантовые приборы и устройства», «Квантовая радиофизика» по специальностям «Физика и техника оптической связи» и «Радиофизика и электроника». Рассмотрены физические основы, принцип действия и характеристики твердотельных, газовых и полупроводниковых лазеров, вопросы управления их параметрами. Изложены физические основы и характеристики элементов оптоэлектронных приборов.
УДК 621.378.1 + 621.383.4 ББК 32.86
ISBN ãАкманов А.Г., Шакиров Б.Г., 2003 г.
ã БашГУ, 2003 г.
ВВЕДЕНИЕ Под квантовой электроникой как областью науки и техники понимается наука, изучающая теорию и метод генерации и усиления электромагнитных волн путем индуцированного излучения в термодинамически неравновесных квантовых системах (атомы, молекулы, ионы), свойства получаемых таким образом генераторов и усилителей и их применения. Основу квантовой электроники составляют физические положения, сформулированные еще в 1916 г. А. Эйнштейном, который теоретически предсказал существование индуцированного излучения и указал на его особое свойство - когерентность вынуждающему излучению. Возможность создания квантовых приборов была обоснована в начале 50-х годов. В 1954 г. в Физическом Институте АН СССР (Прохоров А. М., Басов Н, Г.) и в Колумбийском Университете (Таунс Ч.) были разработаны молекулярные квантовые генераторы (или мазеры1) СВЧ диапазона. Следующий, естественный для развития квантовой электроники шаг был сделан в направлении создания квантовых приборов оптического диапазона. Теоретическое обоснование такой возможности (Таунс Ч., Шавлов А., 1958 г.), предложение открытого резонатора в качестве колебательной системы в оптическом диапазоне (Прохоров А.М, 1958 г.) стимулировали экспериментальные исследования. В 1960 г. был создан лазер1 на рубине (Мейман Т., США), в 1961 г. - лазер на смеси гелия с неоном (Джаван А., США), а в 1962 г. - первые полупроводниковые лазеры (США, СССР).
Оптоэлектроника (ОЭ) – это область науки и техники, связанная с разработкой и применением электронно-оптических устройств и систем для передачи, приема, обработки, хранения и отображения информации. В зависимости от характера оптического сигнала различают когерентную и некогерентную оптоэлектронику. Когерентная ОЭ базируется на использовании источников лазерного излучения. К некогерентной ОЭ относят дискретные и матричные некогерентные излучатели и построенные на их основе индикаторные устройства, а также фотоприёмные устройства, оптопары, оптронные интегральные микросхемы и др.
Лазерное излучение обладает следующими свойствами: 1. Временная и пространственная когерентность. Время когерентности может составить до 10-3 с, что соответствует длине когерентности порядка 105 м (lког=c 2. Строгая монохроматичность ( 3. Большая плотность потока энергии. 4. Очень малое угловое расхождение в среде. КПД лазеров колеблется в широких пределах – от 0,01% (для гелий-неонового лазера) до 75% (для полупроводникового лазера), хотя для большинства лазеров КПД составляет 0,1-1 %. Необычные свойства лазерного излучения находят в настоящее время широкое применение. Применение лазеров для обработки, резания и микросварки твердых материалов оказывается экономически более выгодным. Лазеры применяются для скоростного и точного обнаружения дефектов в изделиях, для тончайших операций (например, луч СО2-лазера в качестве бескровного хирургического ножа), для исследования механизма химических реакций и влияния на их ход, для получения сверхчистых веществ. Одним из важных применений лазеров является получение и исследование высокотемпературной плазмы. Эта область их применения связана с развитием нового направления – лазерного управляемого термоядерного синтеза. Лазеры широко применяются в измерительной технике. Лазерные интерферометры используются для сверхточных дистанционных измерений линейных перемещений, коэффициентов преломления среды, давления, температуры.
Широкое распространение лазерные источники излучения получили в технике связи.
ФИЗИЧЕСКИЕ ОСНОВЫ ЛАЗЕРОВ
Усиление световой волны в лазерах основано на явлении индуцированного излучения фотона возбужденной частицей вещества (атомом, молекулой). Чтобы основную роль играло индуцированное излучение, необходимо перевести рабочее вещество (усиливающую среду) из равновесного состояния в неравновесное, при котором создана инверсия населенностей энергетических уровней. В качестве колебательной системы в лазерах используется так называемой открытый резонатор, представляющий собой систему из двух высокоотражающих зеркал. При помещении между ними рабочего вещества создается условие для многократного прохождения усиливаемого излучения через активную среду, и таким образом реализуется положительная обратная связь. Процесс возбуждения активной среды с целью создания в ней инверсии населенностей называется накачкой, а физическая система, обеспечивающая этот процесс - системой накачки. Таким образом, в структурной схеме любого типа лазера можно выделить три основных элемента: активную среду, систему накачки и открытый резонатор. В соответствии с этим в I главе излагаются основы теории квантового усиления и генерации при взаимодействии светового излучения с веществом, методы накачки и теория открытого резонатора. Оптическое излучение
Оптическим излучением или светом называют электромагнитные волны, длины волн которых заключены в интервале от единиц нанометров до сотен микрометров. Помимо воспринимаемого человеческом глазом видимого излучения (l =0,38-0,76 мкм), различают ультрафиолетовое (l =0,01-0,38 мкм) и инфракрасное (l =0,78-100 мкм) излучения. Напомним некоторые положения и формулы волновой и квантовой оптики. Волновая оптика базируется на уравнениях классической электродинамики, основу которой составляют уравнения Максвелла: [ [ D= ε0e E, B= μ0m H, (1.2) где e – относительная диэлектрическая, m - относительная магнитная проницаемости среды, e0 – электрическая, m0 – магнитная постоянные. Система (1.1) сводится к волновому уравнению для
где с= Объемная плотность энергии, переносимой электромагнитной волной, дается формулой: r=(1/2)ε0e E2+ (1/2)μ0m H2= ε0e E2. (1.6) Спектральная объемная плотность энергии rn определяетсясоотношением: Модуль вектора Умова-Пойнтинга определяет плотность потока световой энергии, Под интенсивностью света понимается усредненный по времени поток энергии Процессы поглощения и испускания света могут быть объяснены только в рамках квантовой оптики, которая рассматривает оптическое излучение в виде потока элементарных частиц – фотонов, не имеющих массы покоя и электрического заряда, обладающих энергией E ф =hn, импульсом p= h k и движущихся со скоростью света.
Плотность потока фотонов F=I/(hn)=ru/(hn) (1.10) где [ hn ]=Дж, [ F ]=1/(м2 с). Спонтанные переходы Если атом (или молекула) находится в состоянии 2 в момент времени t=0, то существует конечная вероятность того, что он перейдет в состояние 1, испустив при этом квант света (фотон) с энергией hn21=(E2-E1) (рис.1.2а). Этот процесс, происходящий без взаимодействия с полем излучения, называется спонтанным переходом, а соответствующее излучение – спонтанным излучением. Вероятность спонтанных переходов пропорциональна времени, т.е. (dw21)сп=A21dt, (1.14) где А21 – коэффициент Эйнштейна для спонтанного излучения и определяет вероятность перехода в единицу времени, [A21]=1/c. Предположим, что в момент времени t населенность уровня 2 составляет величину N2. Скорость перехода этих атомов на нижний уровень вследствие спонтанного излучения пропорциональна вероятности перехода А21 и населенности уровня, с которого происходит переход, т.е. (dN2/dt)сп=-A21N2. (1.15) Из квантовой механики следует, что спонтанные переходы происходят из данного состояния только в состояния, лежащие по энергии ниже, т.е. из состояния 1 в состояние 2 спонтанных переходов нет. Вынужденные переходы
Рассмотрим взаимодействие группы идентичных атомов с полем излучения, плотность энергии которого распределена равномерно по частотам вблизи частоты перехода. При воздействии на атом электромагнитного излучения резонансной частоты (n=ν21=(E2-E1)/h) существует конечная вероятность того, что атом перейдет из состояния 1 на верхний уровень 2, поглощая при этом квант электромагнитного поля (фотон) с энергией hn (рис.1.2б). Разность энергий (E2-E1) необходимая для того, чтобы атом совершал такой переход, берется из энергии падающей волны. В этом заключается процесс поглощения, который можно описать с помощью скоростного уравнения (dN1/dt)п=W12N1=rnB12N1, (1.16) где N1 – населенность уровня 1, W12=rvB12 – вероятность поглощения в единицу времени, rv – спектральная объемная плотность энергии падающего излучения, В12 – коэффициент Эйнштейна для поглощения. Используется также другое выражение для вероятности W12 в виде: W12=s12F, (1.17) где F – плотность потока падающих фотонов, s12 – величина, называемая сечением поглощения, [s12]= м2. Предположим теперь, что атом первоначально находится на верхнем уровне 2 и на вещество падает волна с частотой n=n21. Тогда существует конечная вероятность того, что эта волна инициирует переход атома с уровня 2 на уровень 1. При этом разность энергий (E2-E1) выделится в виде электромагнитной волны, которая добавится к энергии падающей волны. Это и есть явление вынужденного (индуцированного) излучения.
Процесс вынужденного излучения можно описать с помощью скоростного уравнения: (dN2/dt)вын=W21N2=rnB21N2, (1.18) где N2 – населенность уровня 2, W21=rvB21 – вероятность вынужденного перехода в единицу времени, B21- коэффициент Эйнштейнадлявынужденного перехода. И в этом случае для вероятности перехода справедливо соотношение: W21=s21F, (1.19) где s21 – сечение вынужденного излучения для перехода 2→1. Между процессами спонтанного и вынужденного излучения имеется принципиальное отличие. Вероятности индуцированных переходов пропорциональны спектральной объемной плотности электромагнитного поля, а спонтанных от внешнего поля не зависят. В случае спонтанного излучения атом испускает электромагнитную волну, фаза которой не имеет определенной связи с фазой волны, излученной другим атомом. Более того, испущенная волна может иметь любое направление распространения. В случае же вынужденного излучения, поскольку процесс инициируется падающей волной, излучение любого атома добавляется к этой волне в той же фазе. Падающая волна определяет также поляризацию и направление распространения испущенной волны. Таким образом, с ростом числа вынужденных переходов интенсивность волны возрастает, в то время как ее частота, фаза, поляризация и направление распространения остаются неизменными. Другими словами, в процессе вынужденных переходов из состояния E2 в состояние E1 происходит когерентное усиление электромагнитного излучения на частоте n21=(E2-E1)/h. Разумеется, при этом происходят и обратные переходы E1®E2 с поглощением электромагнитного излучения.
Спонтанное излучение Интегрируя выражение (1.15) по времени с начальным условием N2(t=0)=N20 получим: N2(t)=N20exp(-A21t). (1.20) Мощность спонтанного излучения находится перемножением энергии фотона hν21 на количество спонтанных переходов в единицу времени: Pсп=hν21 A21 N2 (t)V=Pсп0exp(-A 21t) (1.21) где Pсп0=hn21 A21 N20 V, V – объем активной среды. Введем понятие о среднем времени жизни атомов в возбужденном состоянии относительно спонтанных переходов. В рассматриваемой двухуровневой системе атомы, которые покидают возбужденное состояние 2 за время от t до t+Dt, очевидно, находились в этом состоянии на протяжении времени t. Число таких атомов равно N2A21Dt. Тогда их средняя продолжительность жизни в возбужденном состоянии определяется соотношением:
Представим формулу (1.22) в виде:
Величину tсп можно найти экспериментально, поскольку она фигурирует как параметр в законе затухания спонтанной люминесценции, определяемой формулой (1.21 а).
Доплеровское уширение В газах движение излучающих молекул относительно наблюдателя приводит к уширению линии за счет эффекта Доплера. Если скорость молекул равна u, то частота излучения, регистрируемая наблюдателем, рассчитывается по формуле:
где с - скорость света, n0 - истинная частота атомного перехода (u<<c), а выбор знака зависит от того, в какую сторону движется молекула. В газе атомы движутся с беспорядочно направленными скоростями, зависящими от температуры Т и распределенными в соответствии с законом Максвелла: где Распределение частиц в газе по скоростям в результате эффекта Доплера определяет частотное распределение в излучении атомов, т.е. можно написать где g(n) функция формы линии излучения. Из (1.33) и (1.35) получаем g(n) =(c/n0)p(u). Подставив вместо где D nТ=n0u0/с - доплеровский сдвиг частоты для частиц со средней тепловой скоростью. Формула (1.36) соответствует гауссовой форме линии излучения (что в формуле отмечено индексом «Г»). Из условия Проведем сравнение линий излучения гауссовой и лоренцевой форм при их одинаковой ширине. Считая ∆νл=∆νГ. из (1.31) находим максимальное значение функции Аналогично из (1.36) На рис.1.5 построены графики лоренцевой и гауссовой линии излучения, приведенные к одинаковой ширине.
Как видно из графика при одинаковых ширинах гауссова кривая заострена сильнее лоренцевой 1.5 Коэффициенты Эйнштейна. Рассмотрим связь между коэффициентами А21, В12 и В21 используя термодинамический поход Эйнштейна. Предположим, что рассматриваемая среда помещена в полость (абсолютно черное тело) объемом V, стенки которой поддерживаются при температуре Т (термостат). Как только система достигает термодинамического равновесия, в ней установится излучение, спектральная объемная плотность которого
где множитель Предположим, что квантовый ансамбль, находящийся в полости, является двухуровневой системой (рис.1.6). В такой квантовой системе, наряду со спонтанным излучением, будут происходить процессы вынужденного излучения и поглощения
Количество переходов 2→1 в единицу времени составляет величину (А21+ρνВ21)N2, а количество обратных переходов 1→2 равно ρν В12 N1. Поскольку система в целом пребывает в состоянии термодинамического равновесия, число переходов с уровня 1 на уровень 2 должно уравновешивать число переходов с уровня 2 на уровень 1, т.е.:
Кроме того, согласно статистике Больцмана:
Из этих двух выражений получаем: Эйнштейн далее постулировал, что излучение, испускаемое или поглощаемое атомами при переходах между рассматриваемыми энергетическими состояниями, должно также подчиняться закону излучения Планка (1.40), так как атомы в рассматриваемой полости находятся в тепловом равновесии с окружающей средой. Для согласования с формулой Планка необходимо выполнение следующих двух условий (при ν=ν21): B12=B21=B (1.44)
Из формулы (1.44) следует, что вероятности поглощения и вынужденного излучения, связанные с излучением абсолютного черного тела, равны друг другу: W12=W21 (1.44a) Соотношение (1.45) позволяет вычислить коэффициент А21, если известен коэффициент В вынужденного излучения в поле излучения черного тела. Таким образом, полная вероятность излучательных переходов в единицу времени равна:
Из формул W12=s12F, W21 =s21F, такжеследует, что s12=s21 (1.44б) Таким образом, термодинамическое рассмотрение показывает равновероятность индуцированных излучения и поглощения и устанавливает количественную связь между коэффициентами Эйнштейна. Квантомеханическое рассмотрение задачи о вычислении вероятности квантового перехода дает следующее значение для W21 :
где Сравнивая (1.47) с формулой Эйнштейна для вероятности перехода W21=rnB21 получим формулу, связывающую коэффициенты Эйнштейна с атомными характеристиками квантового ансамбля:
Квантовое усиление в среде
Рассмотрим монохроматическую плоскую волну частоты n и интенсивности I, соответствующей плотности потока фотонов F, распространяющуюся в направлении z через среду с энергетическими уровнями Е1 и Е2 и населенностями N1 и N2 (двухуровневая модель). При резонансном взаимодействии волны со средой за 1с в единице объема возникает N2W21=N2s21F индуцированных переходов с уровня 2 на уровень 1 и N1W12=N1s12F переходов с уровня 1 на уровень 2. Тогда изменение плотности потока фотонов dF в слое dz (рис.1.7) без учета спонтанных переходов, что справедливо при достаточно больших интенсивностях, определяется выражением: где использовано, что s12=s21=s. Учитывая, что I=Fhn, из (1.50) получаем уравнение для I:
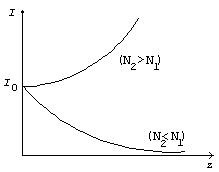
Из (1.51) следует, что в случае N2>N1, dI/dz>0, то есть в среде происходит усиление электромагнитной волны. В случае N2<N1, dI/dz<0, т.е. поглощение. Для среды, находящейся в условиях термодинамического равновесия, Однако если вещество перевести в неравновесное состояние, для которого N2>N1, то среда будет действовать как усилитель. В этом случае говорят, что среда находится в состоянии с инверсией населенностей квантовых уровней. Среда, в которой осуществлена инверсия населенностей, называется активной средой.
Из (1.51) имеем Параметр называется коэффициентом квантового усиления, а формулу (1.52) можно написать в виде: I=I0eGz (1.53) Представляя (1.52) в виде где a - коэффициент поглощения среды, определяемый формулой:
Графики изменения интенсивности волны I(z) в усиливающей (N2>N1) и поглощающей (N2 < N1) средах показаны на рис.1.8. Потери в среде, не связанные с квантовыми переходами (рассеяние, дифракция), учитываются введением коэффициента потерь b и изменение интенсивности волны в общем случае описывается формулой:
Проведем расчет коэффициента поглощения a, исходя из теории квантовых переходов. Используя формулы a=s(N1-N2)=sDN, W12=sF, F=I/hn, I=ρυ запишем: Учтем спектральную зависимость вероятности перехода Wn=W12·g(n)=B12 rn g(n), - где Wn - вероятность индуцированного перехода на частоте n, g(n) – функция формы линии излучения. При этом справедлива и обратная связь: Если индуцирующее квантовый переход излучение монохроматическое, то rn можно представить в виде Тогда где при вычислении интеграла использовано фильтрующее свойство δ – функции. Пусть форма линии излучения является лоренцевой, т.е.
При n=n0, g(n0)=2/(p D nл). Таким образом (1.58а) приобретает вид:
Подставляя (1.59) формулу (1.57) получаем окончательно для
где величина σ называется сечением квантового перехода 2→1:
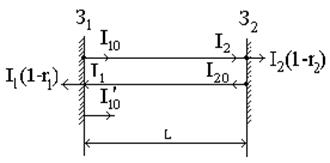
Квантовый генератор (лазер) Для того чтобы квантовый усилитель превратить в квантовый генератор необходимо ввести подходящую положительную обратную связь. В лазере обратную связь получают размещением активной среды между двумя зеркалами с высокими коэффициентами отражения, образующими открытый (или оптический) резонатор. Например, это резонатор Фабри-Перо, представляющий собой систему из двух плоских зеркал З1 и З2, установленных параллельно друг другу, как показано на рис. 1.9.
Рис.1.9 Принципиальная схема лазера.
В этом случае плоская световая волна, распространяющаяся в направлении, перпендикулярном зеркалам, будет поочередно отражаться от них, усиливаясь при каждом проходе через активную среду. Если одно из зеркал сделано частично прозрачным, то на выходе системы можно выделить пучок полезного излучения. Как и в любом автогенераторе, в лазерах генерация возможна лишь при выполнении некоторого порогового условия. Рассмотрим, как показано на рис. 1.10, поэтапно процесс усиления световой волны в активной среде, полностью заполняющей открытый резонатор. Рис.1.10 Процесс усиления света в открытом резонаторе.
Если начальное значение интенсивности у левого зеркала принять равным I10, то за один цикл обхода резонатора интенсивность света В стационарном режиме в уравнении (1.62) должно выполняться условие I10 = I10¢, что приводит к соотношению: 1 =r1 r2 exp [2 (G-b)L ]. (1.63) Из (1.63) следует, что порог достигается тогда, когда коэффициент квантового усиления приближается к некоторому критическому значению, определяемому условием: Gкр = (N2-N1)s = 1 / ( 2 L) ln [ 1/ (r1r2) ] +b (1.64) Физический смысл формулы (1.64) состоит в том, что квантовое усиление в среде должно превышать потери, связанные с полезным излучением за счет выхода излучения через зеркала и потери, учитываемые коэффициентом b. Из формулы (1.64) определяется критическое значение для инверсии населенностей: (N2-N1)кр = Как только достигнута критическая инверсия, генерация начнет развиваться из спонтанного излучения. При этом фотоны, которые спонтанно испускаются вдоль оси резонатора, будут усиливаться в активном элементе.
Метод оптической накачки Идея метода оптической накачки представлена на рис.1.11.
Рис.1.11. Обобщенная схема метода оптической накачки.
Свет от мощной некогерентной лампы (излучение накачки) с помощью соответствующей осветительной системы передается рабочему веществу, которое переводится в состояние с Т<0. Входное электромагнитное излучение (свет), взаимодействуя с таким веществом, усиливается за счет эффекта индуцированного излучения. Рассмотрим используемые в твердотельных лазерах схемы оптической накачки. а) В двухуровневой схеме под действием излучения накачки (рис.1.12) частицы переводятся с нижнего уровня на верхний, одновременно происходят спонтанные переходы. Анализ динамики населенностей в такой системе показывает, что при больших уровнях накачки устанавливается состояние, когда населенности двух уровней выравниваются. Таким образом, используя только два уровня, невозможно получить инверсию населенностей.
б) Идея метода оптической накачки была реализована в многоуровневых схемах накачки.
Рис.1.13 Схемы трехуровневой (а) и четырехуровневой (б) накачки.
В трехуровневой схеме атомы под действием излучения накачки с частотой νнак=ν31 переводятся с основного уровня на уровень 3. Если выбрана среда, в которой атомы оказавшиеся в возбужденном состоянии на уровне 3, быстро переходят на уровень 2*, то в такой среде можно получить инверсию населенностей между уровнями 2* и 1. Существенно при этом, чтобы уровень 2* был метастабильным (долгоживущим), что отмечено значком (*). Рабочим (лазерным) является переход 2*→1, определяющий частоту (длину волны) излучения лазера: ν21=(Е2-Е1)/h. По аналогичной схеме работает и четырехуровневая схема, с тем отличием, что в этом случае свойством метастабильности должен обладать уровень 3*, рабочим является переход 3*→2, определяющий частоту излучения лазера: ν32=(Е3-Е2)/h. Сравнение трех и четырехуровневых схем накачки показывает, что более эффективной является четырехуровневая схема. Действительно, в этой схеме инверсия населенностей между третьим и вторым уровнями достигается значительно легче из–за относительно малой населенности второго уровня. В трехуровневой схеме для получения инверсии населенностей между вторым и первым уровнями необходимо перевести на второй уровень более половины атомов, первоначально находившихся на первом уровне. В результате, пороговый уровень мощности накачки, при которой начинается генерация в лазере, для четырехуровневой схемы примерно на порядок ниже, чем у трехуровневой.
Оптические резонаторы
В качестве колебательной системы в генераторах радиодиапазона применяется колебательный контур, а в СВЧ диапазоне - объемные резонаторы, представляющие собой отрезки пустого металлического волновода прямоугольной или цилиндрической формы. При этом размеры для объемного резонатора L порядка длины волны При дальнейшем увеличении частоты и переходе в миллиметровый или оптический диапазон изготовление объемных резонаторов столь малых размеров становится технологически невозможным. Кроме того, с уменьшением линейных размеров резко падает добротность резонатора. Поэтому для инфракрасного и оптического диапазона вместо объемного резонатора А.М. Прохоровым был предложен открытый резонатор, представляющий собой систему из двух зеркальных поверхностей, установленных на расстоянии L друг от друга. В такой системе L>>
Рис.1.16.Колебательные системы для радио (а), СВЧ (б) и оптического диапазона волн (в).
В общем случае открытый резонатор (ОР) представляет собой систему из двух зеркальных поверхностей сферической формы (рис.1.17.), характеризующийся следующими основными параметрами:1)Радиусы кривизны зеркал R1 и R2 с центрами в точках О1 и О2, расположенных на оптической оси ОО’; 2)База резонатора L; 3)Коэффициенты отражения зеркал по интенсивности r1 и r2; 4) g-параметры g1=1-L/R1, g2=1-L/R2
Рассмотрим в общем виде картину физических процессов при распространении электромагнитной волны в пассивном открытом резонаторе, содержащим между зеркалами однородную, изотропную и пассивную диэлектрическую среду. При построении теории ОР определяющим являются дифракционные потери, связанные с дифракцией электромагнитного поля на краях зеркал, имеющих конечные размеры. Количественно дифракционные потери оцениваются числом Френеля Nф, определяющим число зон Френеля, укладывающихся на поверхности одного из зеркал, если смотреть из центра другого. При больших числах Френеля (Nф>>100) дифракционными потерями можно пренебречь и использовать для анализа процессов в резонаторе метод геометрической оптики и простейшую волновую теорию. В геометрическом приближении, пользуясь понятием светового луча, можно получить условие устойчивости открытого резонатора. Волновая теория позволяет найти частотный спектр (собственные типы колебаний или продольные моды) открытого резонатора и получить первоначальное представление о распределении поля на поверхности зеркал. Однако наиболее общей и полной является дифракционная теория ОР, в рамках которой можно получить информацию как о частотном спектре (продольные моды), так и пространственном распределении поля в поперечном направлении (поперечные моды). Дифракционная теория
Строгое рассмотрение электромагнитного поля в открытом резонаторе основывается на системе уравнений Максвелла с заданными граничными условиями на зеркалах. Лазерные резонаторы имеют ту особенность, что их характерные размеры (длина резонатора, радиусы кривизны и апертуры зеркал) намного превышают длину волны излучения. Исходя из этого, можно считать, что электромагнитное поле в резонаторе является поперечным, однородно поляризованным. Для вычисления его стационарного распре
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 775; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.229.225 (0.018 с.) |

 ког), т.е. на семь порядков выше, чем для обычных источников света.
ког), т.е. на семь порядков выше, чем для обычных источников света. <10-11 м).
<10-11 м). E ]=rot E =
E ]=rot E = 


 (1.1) где Е, D, Н, B – векторы напряженности и индукции соответственно электрического и магнитного полей (система (1.1) написана для случая отсутствия токов и зарядов в среде). В однородной изотропной среде D и B связаны с полями E и H соотношениями (в системе СИ):
(1.1) где Е, D, Н, B – векторы напряженности и индукции соответственно электрического и магнитного полей (система (1.1) написана для случая отсутствия токов и зарядов в среде). В однородной изотропной среде D и B связаны с полями E и H соотношениями (в системе СИ): (или
(или  ):
): 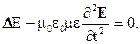 (1.3) Уравнение (1.3) имеет решение
(1.3) Уравнение (1.3) имеет решение 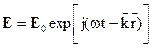 , (1.4) которое описывает плоскую волну, распространяющуюся в направлении, определяемым волновым вектором
, (1.4) которое описывает плоскую волну, распространяющуюся в направлении, определяемым волновым вектором  с фазовой скоростью:
с фазовой скоростью: (1.5)
(1.5) - скорость света в вакууме. Для немагнитной среды m=1, n=
- скорость света в вакууме. Для немагнитной среды m=1, n= 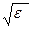 и для скорости волны получим:
и для скорости волны получим: 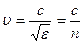 (1.5а)
(1.5а) (1.7)
(1.7)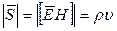 (1.8)
(1.8) .
. (1.9)
(1.9) (1.22)
(1.22) (1.21 а)
(1.21 а)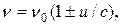 (1.33)
(1.33)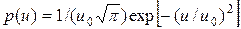 , (1.34)
, (1.34)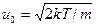 - средняя тепловая скорость атомов с массой m, k - постоянная Больцмана.
- средняя тепловая скорость атомов с массой m, k - постоянная Больцмана. (1.35)
(1.35)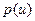 формулу (1.34), имеем:
формулу (1.34), имеем: 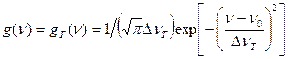 , (1.36)
, (1.36) определяется ширина линии излучения:
определяется ширина линии излучения: 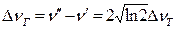 (1.37)
(1.37) (1.38)
(1.38)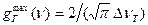 . Подставив вместо
. Подставив вместо  его значение из формулы (1.37), получим:
его значение из формулы (1.37), получим: 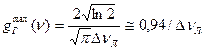 (1.39)
(1.39)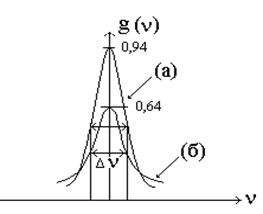
 определяется формулой Планка:
определяется формулой Планка: (1.40)
(1.40)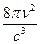 определяет число типов колебаний в единице объема излучающей полости, а величина
определяет число типов колебаний в единице объема излучающей полости, а величина 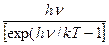 дает среднюю энергию, приходящуюся на один тип колебаний.
дает среднюю энергию, приходящуюся на один тип колебаний.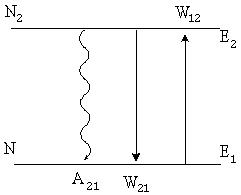
 (1.41)
(1.41)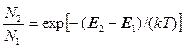 (1.42)
(1.42)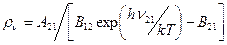 (1.43)
(1.43)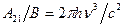 (1.45)
(1.45) (1.46)
(1.46)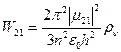 , (1.47)
, (1.47)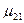 - матричный дипольный момент атома.
- матричный дипольный момент атома.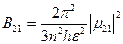 (1.48)
(1.48)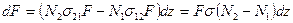 (1.50)
(1.50)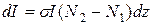 (1.51)
(1.51)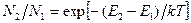 , т.е.
, т.е. 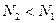 . Таким образом, такая среда поглощает излучение на частоте n, что обычно и происходит.
. Таким образом, такая среда поглощает излучение на частоте n, что обычно и происходит.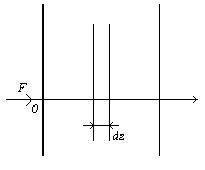
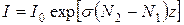 , где I0=I(z=0) (1.52)
, где I0=I(z=0) (1.52)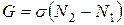 (1.52a)
(1.52a) , приходим к известному закону Бугера
, приходим к известному закону Бугера 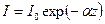 , (1.54)
, (1.54)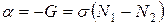 =
= 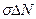 . (1.55)
. (1.55) (1.55 а)
(1.55 а)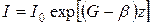 . (1.56)
. (1.56)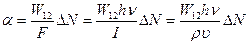 (1.57)
(1.57) . (1.58)
. (1.58)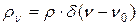 .
. (1.58а)
(1.58а)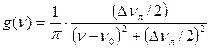 .
.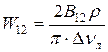 (1.59)
(1.59) :
: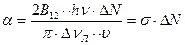 , (1.60)
, (1.60)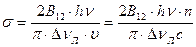 (1.61)
(1.61)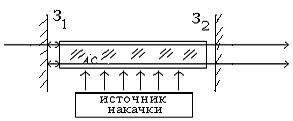
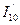 , отраженного от зеркала З1 приобретает значение: I10¢=I20 r1 exp [ (G-b) L ] =r1 r2 I10 exp [ 2(G-b) L ] (1.62)
, отраженного от зеркала З1 приобретает значение: I10¢=I20 r1 exp [ (G-b) L ] =r1 r2 I10 exp [ 2(G-b) L ] (1.62) (1.65)
(1.65)



 .
.
 5)Число Френеля Nф= а1а2/λL, где а1 и а2 диаметры зеркал.
5)Число Френеля Nф= а1а2/λL, где а1 и а2 диаметры зеркал.


