Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая теория открытого резонатораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
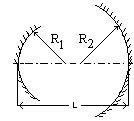
Рассмотрим общий случай резонатора, состоящего из двух сферических зеркал, имеющих радиусы R1 и R2 и расположенных друг от друга на расстоянии L. В приближении геометрической оптики внутри резонатора рассматривается луч, выходящий из т. Р0 с координатой r0 и углом α0. После последовательных отражений от двух зеркал резонатора луч приходит в т. Р1 с координатой r1 и углом α1. Пользуясь матричным методом, можно найти условие устойчивости открытого резонатора. Если при любом выборе исходной точки (r0,α0), произвольная точка (rn,αn) не будет удаляться на бесконечно большое расстояние от оси, то резонатор считается устойчивым. Это означает, что луч претерпевает большое число отражений от зеркал, прежде чем он выйдет из резонатора. В конечном итоге условие устойчивости резонатора сводится к выполнению неравенства: где g1=1-L/R1, g2=1-L/R2 (1.97)
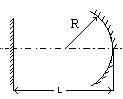
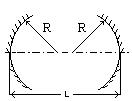
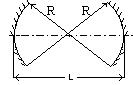
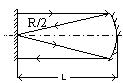
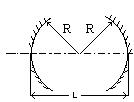
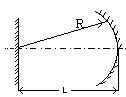
На рис. 1.27 приведена диаграмма в координатах g1 и g2, соответствующая уравнению (1.96). Заштрихованные области определяют устойчивые конфигурации открытого резонатора. Особый интерес представляет класс сферических резонаторов, которым на рисунке соответствуют точки на прямой линии АС, составляющей угол 450 с осями g1 и g2. Эта прямая описывается уравнением g1=g2 (так что R1=R2), а соответствующие ей резонаторы составлены из зеркал, имеющих одинаковые радиусы кривизны (симметричный резонатор). Из всех симметричных резонаторов рассмотрим более подробно те, которым соответствуют на рис. точкам А, B и C. Из приведенной ниже таблицы следует, что точке А соответствует концентрический резонатор (R=2L), точке В - конфокальный (R =L), а точке С - плоский резонатор (R=¥). Следовательно, все эти три типа резонаторов лежат на границе, разделяющей устойчивую и неустойчивую области. В связи с этим часто используют не конфокальный, а квазиконфокальный резонатор, в котором расстояние между зеркалами увеличивают или уменьшают по сравнению с расстоянием, которое используется в конфокальном резонаторе. Другую конфигурацию, которую можно использовать, чтобы избежать неустойчивой области, представляет собой полуконфокальный резонатор (R1=¥ и R2=2L).
Типы оптических резонаторов Таблица 1.1.
Селекция типов колебаний
В оптических резонаторах может одновременно возбуждаться большое число собственных колебаний. Вследствие этого лазер обычно излучает целый набор различных частот, которые лежат внутри линии люминесценции активного вещества (рис.2.14). Каждому типу колебаний в резонаторе соответствует определённое значение частоты и распределение поля на поверхности зеркал. Поэтому при наличии большого числа поперечных и продольных типов колебаний спектр излучения состоит из множества частот, структура поля является сложной, а диаграмма направленности имеет изрезанную форму. Когда генерируются колебания только одного низшего поперечного типа TEM00q, в спектре остаются лишь частоты, соответствующие продольным колебаниям, поле на зеркалах описывается функцией Гаусса, диаграмма излучения сужается и становится гладкой. Многомодовый режим работы генератора значительно ухудшает когерентность и монохроматичность излучения, а также искажает и расширяет его диаграмму направленности. Для большинства научных и практических целей необходимо, чтобы оптический генератор излучал колебания только основного типа и одной частоты. В связи с этим принимаются специальные меры подавления нежелательных типов колебаний высших порядков. В многомодовом режиме мощность излучения сложным образом распределяется по различным типам колебаний, так что в основном типе излучается лишь малая часть общей мощности. При подавлении колебаний высших порядков внешняя энергия преобразуется в основной тип колебаний, и, хотя общая энергия излучения не увеличивается, мощность, сосредоточенная в этом одном типе колебаний, заметно возрастает. Селекция поперечных типов колебаний. Подавление нежелательных поперечных типов колебаний достигается созданием в оптическом резонаторе условия, при котором дифракционных потерь для колебаний высших порядков становится больше, чем для колебаний основного типа TEM00q. Это можно осуществить либо подбором специальной конфигурации резонатора, либо введением в резонатор оптических элементов (линз, диафрагм), либо наклоном зеркал. Рассмотрим в качестве примера метод селекции поперечных мод с помощью диафрагмы круглой формы установленной на оптической оси резонатора
Рис.1.28. Схема селекции поперечных мод диафрагмой.
Как видно из рисунка 1.26 распределение поля в резонаторе для различных типов колебаний таково, что основной тип TEM00q концентрируется вблизи оси резонатора, а поля других высших типов простираются от оси тем дальше, чем более высоким порядкам они соответствуют. Поэтому внесение в резонатор диафрагмы будет сильнее сказываться на потерях высших типов колебаний. Подбором размеров диафрагмы можно добиться подавления всех типов колебаний кроме основного TEM00q. Применяются и другие оптические схемы селекции, основанные на этой идее. Селекция продольных типов колебаний. Количество продольных мод, возбуждающихся в резонаторе, определяется шириной люминесцентной кривой активного вещества, базой резонатора L и уровнем накачки. Изменяя уровень накачки и базу резонатора L можно в определенной степени регулировать ширину спектра генерации лазера
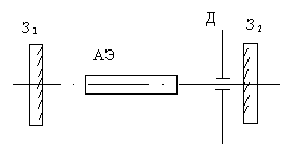
Рис.1.29. Оптическая схема связанных резонаторов. В таких системах, по сравнению с обычным двухзеркальным резонатором, могут возбуждаться неэквидистантные по частоте продольные моды, относительный коэффициент усиления которых зависит от свойств и настройки резонатора. Подбором длин резонаторов L, L1 и L2, а также коэффициента связи между ними можно добиться селективного возбуждения одного или нескольких продольных мод, подавив или существенно ослабив все остальные. На практике наиболее распространенной является схема, когда съюстированные зеркала З2 и З3 расположены плотно друг к другу. В результате такая система образует выходное зеркало являющееся селективным резонатором Фабри-Перо, образованным несколькими отражающими зеркальными поверхностями.
ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ Исторически твердотельные лазеры стали первыми квантовыми генераторами когерентного оптического излучения.Их широкое распространение обусловлено тем, что твердотельные лазеры позволяют получать мощное когерентное излучение от УФ до ИК-области спектра, работать как в импульсном, так и непрерывном режимах. В настоящее время генерация получена на большом числе активных сред (несколько сот), но практическое значение имеют сравнительно небольшое число т/т лазеров: на рубине (l = 0,69 мкм), неодимовые - на стекле и гранате (l ≈1,06 мкм), а также лазеры на кристалле ГСГГ, александрите и эрбиевые. Основу активной среды (АС) твердотельного лазера составляет матрица (диэлектрический кристалл либо стекло), в которую введены ионы примесей - активатора. Именно энергетические уровни активатора используются для создания инверсной населенности и получения эффекта квантового усиления. Относительная концентрация активных центров составляет в т/т рабочих веществах доли или единицы процента от полного числа атомов в среде. Однако абсолютная концентрация активных центров составляет величину 1017-1020 см-3, что соответствует большим коэффициентам квантового усиления. Матрица непосредственно не участвует в физических процессах, приводящих к генерации, но ее вещество определяет технические свойства АС. Физические свойства AC определяются в основном активатором. Перечислим некоторые требования, которым должны удовлетворять твердые вещества, используемые в качестве АС лазеров. 1. Вещество должно обладать метастабильными уровнями энергии, на которых возможно накопить значительное количество активных атомов. При этом время жизни атомов в метастабильном состоянии должно определяться в основном излучательными переходами, т.е. вероятность безызлучательных переходов, при которых вся энергия возбужденных атомов или ее часть передается кристаллической решетке, должна быть относительной малой. 2. Материал должен обладать широкими полосами поглощения с высоким квантовым выходом люминесценции. Чем шире полоса поглощения материала, тем большая часть излучения источника накачки (например, газоразрядной лампы) используется для возбуждения активных атомов. 3. Активное вещество должно иметь малые потери на частоте генерации, не связанные с резонансным переходом частиц между рабочими уровнями, а также высокое оптическое качество. АЭ изготавливается, как правило, в виде цилиндра диаметром 0.3...2 см и длиной 3...20 см. Для уменьшения потерь на отражение торцевые поверхности АЭ просветляются на рабочей длине волны лазера.
Рубиновый лазер Рубин представляет собой кристалл окиси алюминия Al2O3, в котором часть ионов Al+3 замещена ионами хрома Сr+3 (условная химическая формула рубина α - Al2O3:Cr+3). В такой системе активными центрами являются ионы хрома Сr3+, а матрицей - кристалл a-корунда (a-Al2O3). Чистый корунд Al2O3 является серо-прозрачным материалом. Красный рубин, в котором весовая концентрация ионов Сr+3 составляет ~ 0,5%, как драгоценный камень известен давно. Кристаллы рубина, используемые в лазерах в качестве AC, обычно получают путем выращивания из расплава смеси А12О3 и небольшой части Сr2О3. При весовом содержании хрома всего 0,05%, что соответствует 1,6∙1019 ионов/см3, рубин приобретает бледно-розовую окраску. Кристалл рубина анизотропный, одноосный, величина двулучепреломления Dn=ne-n0 = 0,008. На рис.2.1 представлена схема энергетических уровней Cr+3 в рубине. Главные детали оптического спектра рубина связаны c переходами между энергетическими уровнями Cr+3 как активатора. Эти уровни существенно отличаются от уровней энергии в свободных ионах Cr+3. Происхождение их определяется сильным взаимодействием электронной оболочки 3d группы железа (к которой принадлежит хром) с кристаллическим полем решетки. Представленнаясхема энергетических уровней соответствует трехуровневой схеме накачки.
Рабочим переходом в рубине является переход между уровнями 2Е и 4А2. Состояние 2Е является метастабильным и состоит из двух близких подуровней Излучение накачки поглощается рубином в двух широких полосах, соответствующих переходам активных атомов из основного состояния 4А2 в состояние 4F1 и 4F2 (“синяя” и “зеленая” полосы поглощения). Часть возбужденных атомов из состояний 4F1 и 4F2 снова возвращается в основное состояние 4А2, а большая часть их переходит в метастабильное состояние 2Е. Измерения показали, что для перехода 4F2®4A2 вероятность спонтанных переходов A31 ≈3·105 c-1, в то время как вероятность безызлучательных переходов w32 на уровень 2Е составляет w32 ≈2·107 с-1, что соответствует времени безызлучательного перехода t32 ≈5·10-8 с-1. Верхний уровень рабочего перехода Оценим пороговую населенность метастабильного уровня Dпор=N2-(g2/g1)N1=(1-r)/2s21l (2.1) Полагая r = 0,5; l= 10 см, s21 = 2,5∙10-20 см2, находим Dпор =1018 см-3. Рубиновые образцы, используемые в лазерах, изготавливаются обычно в виде стержней, продольная ось которых составляет с оптической осью С угол в 90° или 60°.
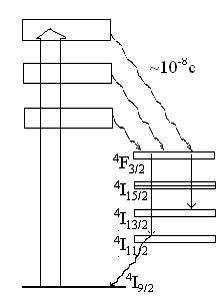
Неодимовые лазеры Неодимовые лазеры являются самыми распространенными из твердотельных лазеров. В них активной средой является кристалл иттрий – алюминиевого граната (Y3Al5O12), в котором часть ионов Y3+ заменена ионами Nd3+ (ИАГ: Nd3+). Также используется фосфатное или силикатное стекло, легированное ионами Nd3+ (стекло: Nd3+). Типичныеуровни легирования для кристалла ИАГ: Nd3+ составляют ~ 1 ат. %, а уровни легирования стекла с Nd3+ ~ 3 вес.% Nd2 O3. Обобщенная схема энергетических уровней Nd3+, характерная для гранатовых и стеклянных матриц, представлена на рис.2.2.
Накачка переводит ионы Nd3+ из основного состояния 4I9/2 в несколько относительно узких полос, играющих роль верхнего уровня. Эти полосы образованы рядом перекрывающихся возбужденных состояний, их положения и ширины отличаются от матрицы к матрице. Из полос накачки осуществляется быстрая передача энергии возбуждения на метастабильный уровень 4F3/2. Время жизни этого уровня составляет 0,2 мс в ИАГ и 0,7 мс в стекле. Наибольшей вероятностью обладает лазерный переход 4F3/2®4I11/2 (l=1,06 мкм). Возможно получить генерацию на переходе 4F3/2®4I13/2 с l=1,32 мкм. Энергетическая щель между состояниями 4I11/2 и 4I9/2, равная примерно 2∙103 см-1, обеспечивает четырехуровневый характер генерации неодимового лазера.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.01 с.) |

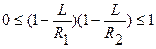 (1.96)
(1.96)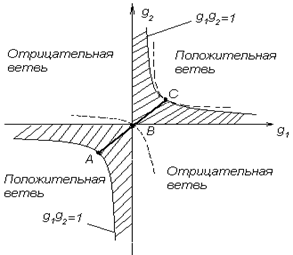
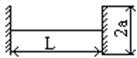
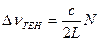 , где N – число возбужденных продольных мод. Однако наиболее универсальный метод селекции продольных мод основан на использовании систем связанных резонаторов (рис.1.29)
, где N – число возбужденных продольных мод. Однако наиболее универсальный метод селекции продольных мод основан на использовании систем связанных резонаторов (рис.1.29)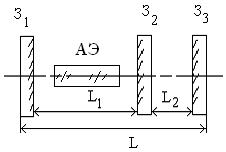
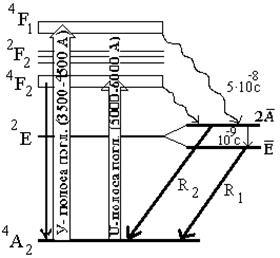
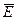 и
и 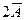 , расстояние между которыми составляет 29 см-1. Переходы между этими подуровнями и основным уровнем 4А2 соответствует линиям излучения R2 и R1 соответственно с длиной волны 6929 Å и 6943 Å при температуре 3000К.
, расстояние между которыми составляет 29 см-1. Переходы между этими подуровнями и основным уровнем 4А2 соответствует линиям излучения R2 и R1 соответственно с длиной волны 6929 Å и 6943 Å при температуре 3000К. =6943 Å. Пусть одно из зеркал резонатора полупрозрачно и имеет коэффициент отражения r, а для второго зеркала коэффициент отражения равен единице. Потери на излучение, пересчитанные на единицу длины, составляют (1-r)/2l, где l - длина активного элемента. Если другие потери несущественны, то, приравнивая эту величину коэффициенту усиления активной среды G=s21(N2-(g2/g1)N1), где s21 - сечение вынужденного перехода, N1, и N2 - населенности соответствующих уровней, а g1 и g2 -кратности вырождения уровней, получим выражение для пороговой населенности:
=6943 Å. Пусть одно из зеркал резонатора полупрозрачно и имеет коэффициент отражения r, а для второго зеркала коэффициент отражения равен единице. Потери на излучение, пересчитанные на единицу длины, составляют (1-r)/2l, где l - длина активного элемента. Если другие потери несущественны, то, приравнивая эту величину коэффициенту усиления активной среды G=s21(N2-(g2/g1)N1), где s21 - сечение вынужденного перехода, N1, и N2 - населенности соответствующих уровней, а g1 и g2 -кратности вырождения уровней, получим выражение для пороговой населенности: