
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории формы и ширины линии излученияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
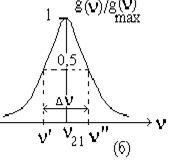
Вероятность спонтанного перехода в единицу времени определяется константой A21, т.е. (dw21cn/dt)νdν=A21g(ν) dν (1.23) где g(ν)-так называемая функция формы линии излучения, определяющая частотное распределение излучения (рис.1.3б). Таким образом, возникают две задачи: 1) исходя из определенной физической модели, найти функцию g(ν); 2) найти ширину линии излучения. При этом под шириной линии излучения понимают интервал частот ∆ν, в пределах которого интенсивность излучения (или нормированная на максимальное значение относительная интенсивность) уменьшается до половинного значения, т.е. ∆ν=ν″-ν΄ (рис.1.3, б).
Рис.1.3 (а) Линия монохроматического излучения, (б) Спектр излучения с учетом уширения квантовых уровней.
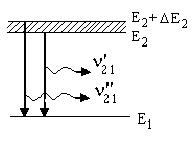
“Естественное” уширение линии излучения Фундаментальной причиной, приводящей к уширению линии излучения, является квантовый характер микрообъектов, подчиняющихся соотношению неопределенности Гейзенберга. Действительно, это соотношение, записываемое в виде ∆p∆x~ħ, где ∆x и ∆p -неопределенности положения частицы и ее импульса, может быть представлено в виде ∆E ∆t~ħ, где ∆E –мера неопределенности энергии частицы, ∆t –время необходимое для проведения такого измерения. Поскольку измерение энергии возбужденного состояния атома должно производится за время ∆t≤τсп, то из соотношения неопределенности получим: ∆E≤ħ/ τсп (1.24) где τсп - среднее время жизни атома в данном состоянии. Так как τсп всегда конечно, то отсюда следует, что энергетические уровни имеют конечную ширину. (рис.1.4)
Из рис. 1.4 имеем: ∆ν=ν”21-ν’21= Таким образом, из (1.25) и (1.24) получаем для оценки ∆ν формулу: Dn Найдем вид функции g(n), определяющей форму линии излучения. В качестве модели излучающего атома в классической физике принимается осциллирующий диполь с радиационным затуханием, уравнение которого имеет вид: где х – координата, g - коэффициент затухания, w0 – собственная частота системы. Решение (1.27) имеет вид: x=Cexp(-gt/2) exp (jw1t), (1.28) где Спектр G(w), соответствующий колебанию x(t), находится с помощью преобразования Фурье:
Отсюда спектральное распределение для интенсивности колебания
Обозначив w0= 2 pn0, w=2pn, g=2pDnл и найдя постоянную С из условия нормировки g(n)= Формула (1.31) соответствует так называемой лоренцевой форме линии излучения, что в формуле обозначено индексом «л». Из условия
Доплеровское уширение В газах движение излучающих молекул относительно наблюдателя приводит к уширению линии за счет эффекта Доплера. Если скорость молекул равна u, то частота излучения, регистрируемая наблюдателем, рассчитывается по формуле: где с - скорость света, n0 - истинная частота атомного перехода (u<<c), а выбор знака зависит от того, в какую сторону движется молекула. В газе атомы движутся с беспорядочно направленными скоростями, зависящими от температуры Т и распределенными в соответствии с законом Максвелла: где Распределение частиц в газе по скоростям в результате эффекта Доплера определяет частотное распределение в излучении атомов, т.е. можно написать где g(n) функция формы линии излучения. Из (1.33) и (1.35) получаем g(n) =(c/n0)p(u). Подставив вместо где D nТ=n0u0/с - доплеровский сдвиг частоты для частиц со средней тепловой скоростью. Формула (1.36) соответствует гауссовой форме линии излучения (что в формуле отмечено индексом «Г»). Из условия Проведем сравнение линий излучения гауссовой и лоренцевой форм при их одинаковой ширине. Считая ∆νл=∆νГ. из (1.31) находим максимальное значение функции Аналогично из (1.36) На рис.1.5 построены графики лоренцевой и гауссовой линии излучения, приведенные к одинаковой ширине.
Как видно из графика при одинаковых ширинах гауссова кривая заострена сильнее лоренцевой 1.5 Коэффициенты Эйнштейна. Рассмотрим связь между коэффициентами А21, В12 и В21 используя термодинамический поход Эйнштейна. Предположим, что рассматриваемая среда помещена в полость (абсолютно черное тело) объемом V, стенки которой поддерживаются при температуре Т (термостат). Как только система достигает термодинамического равновесия, в ней установится излучение, спектральная объемная плотность которого
где множитель Предположим, что квантовый ансамбль, находящийся в полости, является двухуровневой системой (рис.1.6). В такой квантовой системе, наряду со спонтанным излучением, будут происходить процессы вынужденного излучения и поглощения
Количество переходов 2→1 в единицу времени составляет величину (А21+ρνВ21)N2, а количество обратных переходов 1→2 равно ρν В12 N1. Поскольку система в целом пребывает в состоянии термодинамического равновесия, число переходов с уровня 1 на уровень 2 должно уравновешивать число переходов с уровня 2 на уровень 1, т.е.:
Кроме того, согласно статистике Больцмана:
Из этих двух выражений получаем: Эйнштейн далее постулировал, что излучение, испускаемое или поглощаемое атомами при переходах между рассматриваемыми энергетическими состояниями, должно также подчиняться закону излучения Планка (1.40), так как атомы в рассматриваемой полости находятся в тепловом равновесии с окружающей средой. Для согласования с формулой Планка необходимо выполнение следующих двух условий (при ν=ν21): B12=B21=B (1.44)
Из формулы (1.44) следует, что вероятности поглощения и вынужденного излучения, связанные с излучением абсолютного черного тела, равны друг другу: W12=W21 (1.44a) Соотношение (1.45) позволяет вычислить коэффициент А21, если известен коэффициент В вынужденного излучения в поле излучения черного тела. Таким образом, полная вероятность излучательных переходов в единицу времени равна:
Из формул W12=s12F, W21 =s21F, такжеследует, что s12=s21 (1.44б) Таким образом, термодинамическое рассмотрение показывает равновероятность индуцированных излучения и поглощения и устанавливает количественную связь между коэффициентами Эйнштейна. Квантомеханическое рассмотрение задачи о вычислении вероятности квантового перехода дает следующее значение для W21 :
где Сравнивая (1.47) с формулой Эйнштейна для вероятности перехода W21=rnB21 получим формулу, связывающую коэффициенты Эйнштейна с атомными характеристиками квантового ансамбля:
Квантовое усиление в среде
Рассмотрим монохроматическую плоскую волну частоты n и интенсивности I, соответствующей плотности потока фотонов F, распространяющуюся в направлении z через среду с энергетическими уровнями Е1 и Е2 и населенностями N1 и N2 (двухуровневая модель). При резонансном взаимодействии волны со средой за 1с в единице объема возникает N2W21=N2s21F индуцированных переходов с уровня 2 на уровень 1 и N1W12=N1s12F переходов с уровня 1 на уровень 2. Тогда изменение плотности потока фотонов dF в слое dz (рис.1.7) без учета спонтанных переходов, что справедливо при достаточно больших интенсивностях, определяется выражением: где использовано, что s12=s21=s. Учитывая, что I=Fhn, из (1.50) получаем уравнение для I:
Из (1.51) следует, что в случае N2>N1, dI/dz>0, то есть в среде происходит усиление электромагнитной волны. В случае N2<N1, dI/dz<0, т.е. поглощение. Для среды, находящейся в условиях термодинамического равновесия, Однако если вещество перевести в неравновесное состояние, для которого N2>N1, то среда будет действовать как усилитель. В этом случае говорят, что среда находится в состоянии с инверсией населенностей квантовых уровней. Среда, в которой осуществлена инверсия населенностей, называется активной средой.
Из (1.51) имеем Параметр называется коэффициентом квантового усиления, а формулу (1.52) можно написать в виде: I=I0eGz (1.53) Представляя (1.52) в виде где a - коэффициент поглощения среды, определяемый формулой:
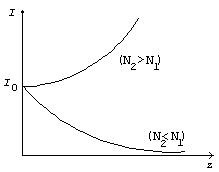
Графики изменения интенсивности волны I(z) в усиливающей (N2>N1) и поглощающей (N2 < N1) средах показаны на рис.1.8. Потери в среде, не связанные с квантовыми переходами (рассеяние, дифракция), учитываются введением коэффициента потерь b и изменение интенсивности волны в общем случае описывается формулой:
Проведем расчет коэффициента поглощения a, исходя из теории квантовых переходов. Используя формулы a=s(N1-N2)=sDN, W12=sF, F=I/hn, I=ρυ запишем: Учтем спектральную зависимость вероятности перехода Wn=W12·g(n)=B12 rn g(n), - где Wn - вероятность индуцированного перехода на частоте n, g(n) – функция формы линии излучения. При этом справедлива и обратная связь: Если индуцирующее квантовый переход излучение монохроматическое, то rn можно представить в виде Тогда где при вычислении интеграла использовано фильтрующее свойство δ – функции. Пусть форма линии излучения является лоренцевой, т.е.
При n=n0, g(n0)=2/(p D nл). Таким образом (1.58а) приобретает вид:
Подставляя (1.59) формулу (1.57) получаем окончательно для
где величина σ называется сечением квантового перехода 2→1:
Квантовый генератор (лазер) Для того чтобы квантовый усилитель превратить в квантовый генератор необходимо ввести подходящую положительную обратную связь. В лазере обратную связь получают размещением активной среды между двумя зеркалами с высокими коэффициентами отражения, образующими открытый (или оптический) резонатор. Например, это резонатор Фабри-Перо, представляющий собой систему из двух плоских зеркал З1 и З2, установленных параллельно друг другу, как показано на рис. 1.9.
Рис.1.9 Принципиальная схема лазера.
В этом случае плоская световая волна, распространяющаяся в направлении, перпендикулярном зеркалам, будет поочередно отражаться от них, усиливаясь при каждом проходе через активную среду. Если одно из зеркал сделано частично прозрачным, то на выходе системы можно выделить пучок полезного излучения. Как и в любом автогенераторе, в лазерах генерация возможна лишь при выполнении некоторого порогового условия. Рассмотрим, как показано на рис. 1.10, поэтапно процесс усиления световой волны в активной среде, полностью заполняющей открытый резонатор. Рис.1.10 Процесс усиления света в открытом резонаторе.
Если начальное значение интенсивности у левого зеркала принять равным I10, то за один цикл обхода резонатора интенсивность света В стационарном режиме в уравнении (1.62) должно выполняться условие I10 = I10¢, что приводит к соотношению: 1 =r1 r2 exp [2 (G-b)L ]. (1.63) Из (1.63) следует, что порог достигается тогда, когда коэффициент квантового усиления приближается к некоторому критическому значению, определяемому условием: Gкр = (N2-N1)s = 1 / ( 2 L) ln [ 1/ (r1r2) ] +b (1.64) Физический смысл формулы (1.64) состоит в том, что квантовое усиление в среде должно превышать потери, связанные с полезным излучением за счет выхода излучения через зеркала и потери, учитываемые коэффициентом b. Из формулы (1.64) определяется критическое значение для инверсии населенностей: (N2-N1)кр = Как только достигнута критическая инверсия, генерация начнет развиваться из спонтанного излучения. При этом фотоны, которые спонтанно испускаются вдоль оси резонатора, будут усиливаться в активном элементе.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.011 с.) |

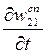 =A21 и в результате такого перехода испускается монохроматическое излучение с частотой
=A21 и в результате такого перехода испускается монохроматическое излучение с частотой 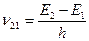 (рис.1.3а). На самом деле происходит уширение линий излучения вследствие различных физических причин, приводящих к конечной ширине энергетического уровня. С учетом этого вероятность перехода в единицу времени и в расчете на единичный интервал частот с испусканием фотона в частотном интервале от ν до ν+dν определяется формулой:
(рис.1.3а). На самом деле происходит уширение линий излучения вследствие различных физических причин, приводящих к конечной ширине энергетического уровня. С учетом этого вероятность перехода в единицу времени и в расчете на единичный интервал частот с испусканием фотона в частотном интервале от ν до ν+dν определяется формулой:
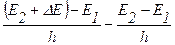 =∆E/h (1.25)
=∆E/h (1.25)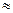 DE/h
DE/h 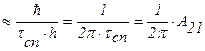 (1.26)
(1.26)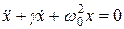 , (1.27)
, (1.27) (при малом g).
(при малом g).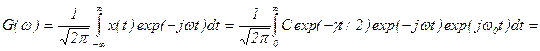
 . (1.29)
. (1.29)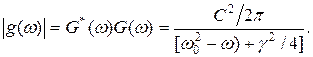 (1.30)
(1.30)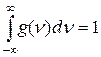 , получаем окончательно:
, получаем окончательно: (1.31)
(1.31) находим значения частот ν” и ν’. Тогда ширина линии излучения определяется соотношением:
находим значения частот ν” и ν’. Тогда ширина линии излучения определяется соотношением: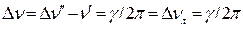
 (1.32)
(1.32)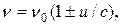 (1.33)
(1.33)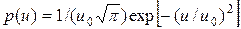 , (1.34)
, (1.34)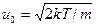 - средняя тепловая скорость атомов с массой m, k - постоянная Больцмана.
- средняя тепловая скорость атомов с массой m, k - постоянная Больцмана. (1.35)
(1.35)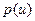 формулу (1.34), имеем:
формулу (1.34), имеем: 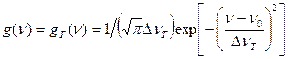 , (1.36)
, (1.36) определяется ширина линии излучения:
определяется ширина линии излучения: 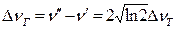 (1.37)
(1.37) (1.38)
(1.38)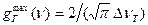 . Подставив вместо
. Подставив вместо  его значение из формулы (1.37), получим:
его значение из формулы (1.37), получим: 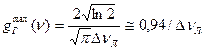 (1.39)
(1.39)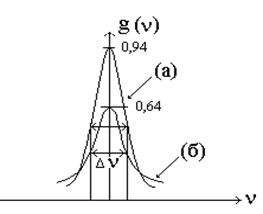
 определяется формулой Планка:
определяется формулой Планка: (1.40)
(1.40)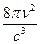 определяет число типов колебаний в единице объема излучающей полости, а величина
определяет число типов колебаний в единице объема излучающей полости, а величина 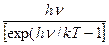 дает среднюю энергию, приходящуюся на один тип колебаний.
дает среднюю энергию, приходящуюся на один тип колебаний.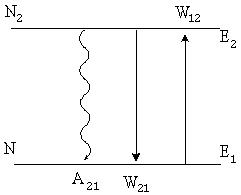
 (1.41)
(1.41)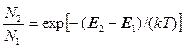 (1.42)
(1.42)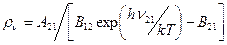 (1.43)
(1.43)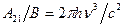 (1.45)
(1.45) (1.46)
(1.46)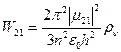 , (1.47)
, (1.47)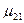 - матричный дипольный момент атома.
- матричный дипольный момент атома.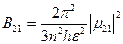 (1.48)
(1.48)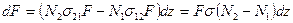 (1.50)
(1.50)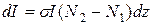 (1.51)
(1.51)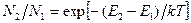 , т.е.
, т.е. 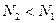 . Таким образом, такая среда поглощает излучение на частоте n, что обычно и происходит.
. Таким образом, такая среда поглощает излучение на частоте n, что обычно и происходит.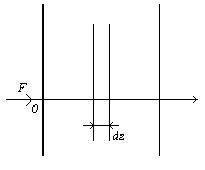
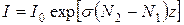 , где I0=I(z=0) (1.52)
, где I0=I(z=0) (1.52)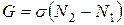 (1.52a)
(1.52a) , приходим к известному закону Бугера
, приходим к известному закону Бугера 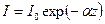 , (1.54)
, (1.54)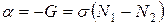 =
= 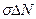 . (1.55)
. (1.55) (1.55 а)
(1.55 а)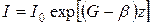 . (1.56)
. (1.56)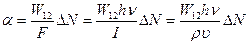 (1.57)
(1.57) . (1.58)
. (1.58)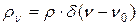 .
. (1.58а)
(1.58а)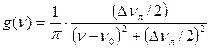 .
.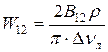 (1.59)
(1.59) :
: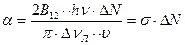 , (1.60)
, (1.60)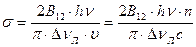 (1.61)
(1.61)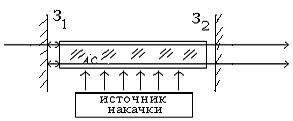
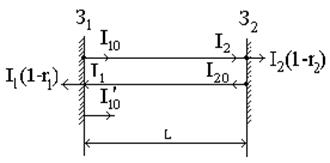
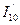 , отраженного от зеркала З1 приобретает значение: I10¢=I20 r1 exp [ (G-b) L ] =r1 r2 I10 exp [ 2(G-b) L ] (1.62)
, отраженного от зеркала З1 приобретает значение: I10¢=I20 r1 exp [ (G-b) L ] =r1 r2 I10 exp [ 2(G-b) L ] (1.62) (1.65)
(1.65)


