
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства теплового излученияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ Заключительный раздел курса общей физики посвящен рассмотрению процессов, которые происходят между объектами, имеющими удивительные так называемые квантовые свойства. Теория этих явлений довольно сложна. С одной стороны, применяемый математический аппарат значительно усложняется по сравнению с рассматриваемой до этого классической физикой. С другой стороны – большая часть затруднений связана с тем, что наше восприятие окружающего мира имеет «классическую» направленность. Многие свойства квантовых частиц, не имея аналогии в классической физике, вообще с трудом поддаются пониманию. Для преодоления этого препятствия требуются последовательность в изучении материала и настойчивость, так как некоторые вопросы корректно усваиваются только после многократных попыток осознать суть изучаемого явления. Данное пособие представляет собой примерный курс лекций, содержащий в логическом порядке основные разделы квантовой механики, атомной, молекулярной и ядерной физики, а также элементы квантовой статистики и зонной теории твердых тел. Темы, систематически вызывающие у студентов наибольшие затруднения, рассмотрены более подробно. Кроме того, учтены современные поправки к развивающимся теориям, описан ряд приборов и устройств, работающих на основе квантовых явлений. Содержание курса подобрано в соответствии с программой базового уровня по дисциплине "Физика" федерального компонента цикла общих математических и естественнонаучных дисциплин для ГОС 3-го поколения, рекомендованной научно-методическим советом по физике Министерства образования и науки Российской Федерации. Пособие может быть использовано для аудиторных занятий и как дополнение к рекомендованным учебникам при самостоятельном изучении третьей части общего курса физики студентами-бакалаврами 1 и 2 курсов инженерно-технических специальностей ВТУЗа. Может быть особенно полезным для экономии лекционного времени за счет обращения в текст пособия. I. КВАНТОВАЯ ПРИРОДА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ ТЕПЛОВОЕ ИЗЛУЧЕНИЕ Закон Стефана-Больцмана. Формула Рэлея-Джинса. Закон смещения Вина К 1884 г. Стефан, основываясь на экспериментальных данных, и Больцман из теоретических соображений получили, что энергетическая светимость RT абсолютно черного тела, связанная с испускательной способностью выражением (1.2), подчиняется следующему закону:
где T – абсолютная температура, σ – константа, получившая название постоянной Стефана-Больцмана, σ = 5,7·10–8 Вт/(м2·К4). Если коэффициент поглощения какого-либо тела отличен от единицы, но постоянен для всех длин волн и зависит только от температуры тела, материала и состояния поверхности, то такое тело называют серым. Понятие серое тело используют как идеализированную модель реальных тел. Закон Стефана-Больцмана (1.11), выведенный для абсолютно черного тела, для серого тела, обладающего поглощательной способностью аТ сер, имеет вид: Попытки получить математическую функцию f(ω,Т) или φ(λ,Т), описывающую спектральное распределение энергии излучения тела, долго не приносили результатов, сколько-нибудь согласующихся с экспериментальными данными. Причиной этого был так называемый «классический подход» к решению данной задачи. Все ученые того времени исходили из соображений классической механики и представлений, что излучение – это волна, распространяющаяся непрерывно. Соответственно энергия, переносимая волной, должна иметь непрерывный спектральный состав, то есть, энергия волны – есть непрерывная функция частоты (или длины волны) излучения. Примером неудачной попытки построить теорию, согласующуюся с опытом, была формула, выведенная Джоном Уильямом Рэлеем и Джинсом. При расчетах они опирались на теорему классической статистики о равномерном распределении энергии по степеням свободы. Рассматривая излучение как электромагнитную волну, было положено, что на каждое колебание приходится две половинки kT, что привело к формуле:
где k = 1,38·10–23 Дж/K – постоянная Больцмана. Эта формула удовлетворительно совпадает с экспериментальными данными (на рис. 1.4. представлены точками) только при больших длинах волн. В области больших частот (малых длин волн) хорошее согласие дает формула Вина, выведенная им в 1893 г. из общих классических принципов:
где α и β – постоянные величины, установленные спустя некоторое время. Вильгельм Вин получил эту формулу, рассмотрев адиабатическое (то есть без теплообмена системы с окружающей средой) сжатие излучения черного тела в цилиндрическом сосуде с зеркальными стенками и зеркальным поршнем. Он учел также, что частота излучения меняется при отражении от двигающегося поршня вследствие эффекта Доплера. Имея вид функции, можно с помощью дифференцирования найти точки экстремумов.
Поскольку λ ≠ ∞, а
Экспериментально найденная константа Выражение (1.17) известно под названием закон смещения Вина – длина волны λmax, соответствующая максимальному значению функции Кирхгофа φ(λ,Т) черного тела, обратно пропорциональна его термодинамической температуре. Другими словами положение максимума кривой зависимости от длины волны интенсивности излучения черного тела (рис. 1.3) зависит от его температуры – чем выше температура, тем сильнее максимум смещается в коротковолновую сторону.
Рис. 1.4. Теоретические кривые спектра теплового излучения и экспериментальные точки Однако ни формула Рэлея-Джинса (1.13), ни формула Вина (1.14) не могли претендовать на истинность. Такое серьезное расхождение теории и эксперимента получило название «ультрафиолетовой катастрофы». Проблема заключалась в том, что согласно формуле Рэлея-Джинса в диапазоне частот от ультрафиолетовых длин волн тело должно испускать огромные потоки энергии и чем меньше длина волны, тем выше должна быть интенсивность излучения. На деле же наблюдается спад поглощательной и испускательной способностей любого тела в области коротких длин волн. Формула была выведена из безупречных термодинамических соображений. Подобный парадокс означал, что фундамент, на котором стояла вся физика, имел серьезный изъян. Для многих физиков это было настоящей «катастрофой», поскольку объяснить такое противоречие они могли только нарушением одного из фундаментальных законов физики – закона сохранения энергии.
Теория Планка Для того, чтобы устранить ошибку, ученым пришлось кардинально изменить взгляд на природу излучения. Первым это сделал Макс Планк. После долгих расчетов, чтобы получить желаемый и напрашивающийся результат, он предположил, что электромагнитное излучение испускается отдельными порциями энергии (квантами). Величина энергии каждого кванта пропорциональна частоте излучения:
Коэффициент ħ был назван постоянной Планка. ħ = h/2π = (6,62·10–34/2π) Дж·с = 1,054·10–34 Дж·с = 0,659·10–15 эВ·c. Таким образом, энергия излучения должна быть кратна n – количеству квантов в потоке излучения и величине E: Тогда, если излучение равновесное, то распределение колебаний по значениям энергии должно подчиняться статистике Больцмана – вероятность того, что энергия колебания частоты ω имеет значение En, должна определяться выражением:
Функция Кирхгофа, полученная согласно этим соображениям, имеет вид:
Это выражение известно под названием формула Планка. Она абсолютно точно согласуется с экспериментальными данными (см. рис. 1.4). Если перейти в рассмотрении задачи от частот к длинам волн, то функция Кирхгофа (1.21) примет вид:
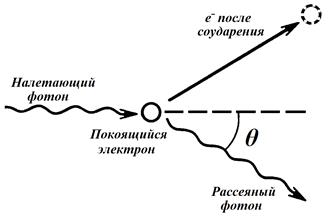
Осуществив необходимые преобразования, из формулы Планка можно получить закон Стефана-Больцмана (1.11) и закон смещения Вина (1.17). С помощью закона Планка был получен аргумент в пользу так называемой теории Большого Взрыва, объясняющей возникновение и продолжающееся расширение Вселенной (согласно современной теории, Вселенная возникла при взрыве с предельно высокой температурой). Считается, что на ранних стадиях своего развития Вселенная была заполнена излучением, спектральный состав которого должен был совпадать с излучением черного тела. С тех пор вселенная расширилась и остыла до ее нынешней температуры Тсовр. То есть, излучение, которое сейчас распространяется во Вселенной, по спектральному составу должно совпадать с излучением черного тела с температурой Тсовр. В 1965 г. Пензиас и Вильсон обнаружили излучение на длине волны 7.35 см, которое падает на Землю с одинаковой интенсивностью во всех направлениях. Вскоре стало ясно, что это излучение может испускать черное тело, появившееся после Большого Взрыва. Результаты измерений свидетельствуют о том, что температура этого черного тела на данный момент составляет 2,7 К. С использованием теории теплового излучения описывают явление, которое сопутствовало бы ядерному взрыву – так называемую «ядерную зиму». Сильный взрыв поднимет в воздух колоссальные массы пыли и сажи. Как близкое к абсолютно черному телу, сажа поглощает почти все солнечное излучение, нагревается и испускает тепловое излучение в обе стороны. В результате на Землю попадает только половина излучения, приходящего от Солнца, так как вторая половина будет излучаться в противоположную от Земли сторону. Согласно расчетам средняя температура Земли снизится на 50 K (это температура ниже точки замерзания воды). Заметим еще один фактор – сажа не является абсолютно черным телом в длинноволновой (инфракрасной) части спектра. Она хорошо поглощает коротковолновое (ультрафиолетовое) излучение, приходящее от Солнца, но пропускает инфракрасное излучение Земли, что приведет к дополнительному остыванию планеты. Процесс прекратится только после рассеивания «черного» облака, однако на это может уйти до 7 лет, после чего начнется постепенное разогревание планеты. Аналогично можно объяснить возникновение парникового эффекта: углекислый газ хорошо пропускает коротковолновое (ультрафиолетовое), но поглощает инфракрасное излучение. Поэтому повышение концентрации CO 2 в атмосфере приведет к задержке и возвращению на Землю все большей доли испущенного ею теплового излучения и постепенному разогреванию Земли. Фотоэффект Наряду с законами теплового излучения в конце XIX в. было открыто оптическое явление, не укладывающееся в рамки законов классической физики. Это явление фотоэлектрического эффекта или просто фотоэффект. Фотоэлектрическим эффектом, или фотоэффектом называют испускание электронов с поверхности твердых и жидких тел под действием света. Ионизация атомов и молекул газа под действием света называется фотоионизацией. Это явление обнаружил Г. Герц 1887. Наблюдая за проскакиванием искры между цинковыми шариками разрядника, он заметил следующее: облучение одного из шариков-электродов ультрафиолетовыми лучами приводит к возникновению искры при более низком напряжении между электродами. В 1888 – 1889 гг. Русский ученый А.Г. Столетов провел подробное исследование фотоэффекта и сформулировал его законы. Для этого он сконструировал установку, состоящую из включенных последовательно в цепь батареи гальванометра Г и конденсатора, одна из пластин которого представляла собой металлическую сетку (рис. 2.1). Свет, проникая сквозь сетку, попадал на сплошную пластину конденсатора. В этом случае гальванометр регистрировал ток. Причем сила тока была тем выше, чем больше освещенность пластины. Столетов также показал, что под действием света с поверхности пластины вылетают отрицательные заряды. Это было очевидно, поскольку появление тока наблюдалось только при освещении отрицательно заряженной пластины.
Рис. 2.1. Схема опыта Столетова Рис. 2.2. Схема опыта Ленарда и Томсона В 1899 г. Ф. Ленард и Дж. Дж. Томсон измерили удельный заряд этих частиц, таким образом, они установили, что отрицательно заряженными носителями являются электроны. Ими был предложен усовершенствованный прибор для исследования фотоэффекта (рис. 2.2). Электроды помещались в специальный баллон, из которого откачивался воздух. Через кварцевое окошко катод K, изготовленный из исследуемого материала, освещался светом. Под действием этого света с поверхности катода выбиваются электроны, и если между катодом и анодом приложено напряжение, электроны могут достигнуть анода. Фототок, возникающий в результате этого, регистрируется гальванометром Г. Напряжение между катодом и анодом можно менять с помощью потенциометра П. Меняя напряжение, можно получить вольт-амперную характеристику (ВАХ) – зависимость фототока i от напряжения между электродами U (рис. 2.3). Чтобы получить достоверную кривую, измерения необходимо проводить при постоянном потоке света Ф. Начиная с некоторого напряжения, ток перестает увеличиваться – фототок достигает насыщения. Насыщение тока наблюдается, когда все электроны, выбитые с катода под действием света, достигают анода. Отличие фототока от нуля при нулевом напряжении свидетельствует о том, что при вылете с поверхности катода электроны имеют некоторую скорость. Если скорость достаточно велика, то электрон может достигнуть анода самостоятельно. Чтобы воспрепятствовать попаданию электрона на второй электрод, то есть не допустить появление фототока, необходимо приложить обратное напряжение Uз, называемое «задерживающим». Измерив «задерживающее» напряжение, можно найти максимальную скорость электронов, выбитых с поверхности катода:
где V, m и e – соответственно скорость, масса и заряд электрона.
Рис. 2.3. Вольт-амперная характеристика фототока Довольно неожиданным для ученых, которые изучали это явление, оказался тот факт, что максимальная скорость электронов не зависит от интенсивности света, а зависит от его частоты – под действием синего света можно получить более быстрые электроны, чем под действием красного света. Классические представления физики не могли объяснить этого – считалось, что чем ярче свет, тем больше должна быть скорость электронов, выбиваемых с поверхности. Вопреки такому взгляду, справедлив первый закон внешнего фотоэффекта: Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности. Поскольку частота света определяет максимальную кинетическую энергию электрона, то при изменении частоты будет меняться значение задерживающего напряжения. На рис. 2.3 видно, что при изменении частоты две кривые с одинаковым значением тока насыщения пересекают горизонтальную ось в разных точках – Uз1 и Uз2. Этот закон можно объяснить, только опираясь на квантовую природу света. Свет, падающий на поверхность катода, представляет собой поток частиц квантов (фотонов). Каждый квант, соударяясь с поверхностью, передает ей свою энергию. Однако энергия нескольких фотонов не накапливается в веществе, чтобы затем «выбросить» в пространство один электрон, обладающий кинетической энергией нескольких фотонов. Суммирование энергии нескольких квантов (двух, трех, очень редко – четырех и больше) возможно только при использовании источников света с высокой плотностью возбуждения. Таким свойством излучения обладают мощные лазеры. Под действием лазерного излучения наблюдается многофотонный фотоэффект. Энергия, расходуемая на выбивание каждого электрона в этом случае равна E = nhν, где n – число суммируемых квантов. Каждый фотон может освободить с поверхности не более одного фотона или же его энергия просто поглотится поверхностью и перейдет в энергию теплового колебания кристаллической решетки. То есть фототок пропорционален числу фотонов в световом потоке или другими словами: Число фотоэлектронов, вырываемых из катода за единицу времени, пропорционально интенсивности света так можно сформулировать второй закон внешнего фотоэффекта. Эта особенность явления также имеет чисто квантовый характер и не может быть объяснена, если рассматривать свет как непрерывную волну. Очевидно, что имея определенное число фотонов, падающих на поверхность, не возможно получить ток больше так называемого тока насыщения (Iн на рис. 2.3). Таким образом, фототок насыщения пропорционален энергетической освещенности катода (на рис. 2.3 ток насыщения для кривых Ф1 и Ф2 имеет различное значение). Кроме того, фотоэффект – процесс практически безынерционный. Это означает, что ток в цепи регистрируется практически мгновенно (t = 10 –9 c) при попадании светового потока на катод, хотя согласно классическим волновым представлениям, энергия светового потока должна постепенно накапливаться у поверхности вещества и спустя некоторое время, сконцентрировавшись на некоторых электронах, заставлять их покидать поверхность. С квантовой точки зрения передача энергии от фотона электрону происходит мгновенно, как при соударении двух тел. Все экспериментальные данные были собраны и объяснены в рамках единой теории Альбертом Эйнштейном. Выведенное им энергетическое уравнение для внешнего фотоэффекта записывается для одного фотона и одного электрона:
Энергия каждого кванта света расходуется на совершение работы выхода, оставшуюся порцию энергии получает выбитый с поверхности вещества электрон в виде кинетической энергии. Vmax соответствует тем электронам, которые находились на поверхности материала. Очевидно, что расположенные более глубоко электроны, если они смогут оторваться от поверхности, будут обладать меньшей скоростью, так как для их выбивания понадобится бóльшая энергия. Параметр работа выхода Авых, входящий в уравнение (2.2), указывает, какую энергию необходимо затратить для преодоления потенциала, удерживающего электрон в веществе. Работа выхода определяется химической природой (для каждого вещества она имеет свое значение), а также состоянием поверхности образца в случае твердых тел. Окисление поверхности или загрязнение ее любым веществом может существенно повлиять на способность электрона покинуть поверхность. Поскольку для осуществления фотоэффекта важно, была ли преодолена сила, удерживающая электрон на поверхности, то решающее значение будет иметь величина энергии кванта света, падающего на поверхность. В связи с этим третий закон внешнего фотоэффекта гласит: Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν0 света, при которой еще возможен внешний фотоэффект. Частота ν0 определяется работой выхода и, следовательно зависит от химической природы вещества и состояния поверхности. Для большинства металлов Авых = 2 ÷ 6 эВ. Выразим из уравнения Эйнштейна частоту света ν0, при которой вылетевший из вещества электрон имеет нулевую скорость (и соответственно нулевую кинетическую энергию):
Таким образом, частота красной границы может лежать за пределами видимого диапазона. Фотоэффект в металлах гарантированно наблюдается под действием ультрафиолетового или рентгеновского излучения. Величину работы выхода можно определить, приняв, что энергия фотона полностью израсходована. Существует еще два типа фотоэффекта: внутренний (протекающий в полупроводниках или диэлектриках) и вентильный (возможный только на границе двух полупроводников или полупроводника и металла). Внутренний фотоэффект заключается в том, что электроны внутри полупроводника или диэлектрика переходят из связанных состояний в свободные без вылета наружу. Это означает, что электроны, которые в обычном состоянии были связаны со своими ядрами, становятся свободными. В результате концентрация носителей тока внутри тела увеличивается, что приводит к возникновению фотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или к возникновению ЭДС. Вентильный фотоэффект является разновидностью внутреннего фотоэффекта. На основе фотоэффекта работают фотоэлементы – приемники излучения, преобразующие энергию этого излучения в электрическую энергию. Современная полупроводниковая технология предоставляет широкий выбор разнообразных фотоэлементов, предназначенных для различных целей – от простейшего регистратора движения до сложнейших устройств, предназначенных для преобразования солнечной энергии в электрическую или визуализации инфракрасного излучения (так называемых приборов ночного видения). Эффект Комптона Наличие у света корпускулярных свойств также подтверждается комптоновским рассеянием фотонов. Эффект назван в честь открывшего в 1923 г. это явление американского физика Артура Холли Комптона. Он изучал рассеяние рентгеновских лучей на различных веществах. Эффект Комптона – изменение частоты (или длины волны) фотонов при их рассеянии. Может наблюдаться при рассеянии на свободных электронах фотонов рентгеновского диапазона или на ядрах при рассеянии гамма-излучения.
Рис. 2.5. Схема установки для исследования эффекта Комптона. Тр – рентгеновская трубка Эксперимент Комптона заключался в следующем: он использовал так называемую линию Кα в характеристическом рентгеновском спектре молибдена с длиной волны λ0 = 0.071нм. Такое излучение можно получить при бомбардировке электронами молибденового анода (рис. 2.5), отрезав излучения других длин волн с помощью системы диафрагм и фильтров (S). Прохождение монохроматического рентгеновского излучения через графитовую мишень (М) приводит к рассеянию фотонов на некоторые углы φ, то есть к изменению направления распространения фотонов. Измеряя с помощью детектора (Д) энергию рассеянных под различными углами фотонов, можно определить их длину волны. Оказалось, что в спектре рассеянного излучения наряду с излучением, совпадающим с падающим, присутствует излучение с меньшей энергией фотонов. При этом различие между длинами волн падающего и рассеянного излучений ∆ λ = λ – λ0 тем больше, чем больше угол, определяющий новое направление движения фотона. То есть на большие углы рассеивались фотоны с бóльшей длиной волны. Этот эффект не может быть обоснован классической теорией: длина волны света при рассеянии изменяться не должна, т.к. под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому должен излучать под любым углом вторичные волны той же частоты. Объяснение эффекту Комптона дала квантовая теория света, в рамках которой процесс рассеяния света рассматривается как упругое столкновение фотонов с электронами вещества. В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения в точности как при упругом столкновении двух тел.
Рис. 2.6. Комптоновское рассеяние фотона Поскольку после взаимодействия релятивистской частицы фотона с электроном последний может получить ультравысокую скорость, закон сохранения энергии необходимо писать в релятивистской форме:
Где hν0 и hν – энергии соответственно падающего и рассеянного фотонов, mc2 – релятивистская энергия покоя электрона – энергия электрона до столкновения, Ee – энергия электрона после столкновения с фотоном. Закон сохранения импульса имеет вид:
где p0 и p – импульсы фотона до и после столкновения, pe – импульс электрона после столкновения с фотоном (до столкновения импульс электрона равен нулю). Возведем в квадрат выражение (2.30) и помножим на с2:
Воспользуемся формулами (2.5) и выразим импульсы фотонов через их частоты: Учитывая, что энергия релятивистского электрона определяется формулой:
и используя закон сохранения энергии (2.8), получим:
Возведем в квадрат выражение (2.13):
Сравним формулы (2.11) и (2.14) и проведем простейшие преобразования:
Частота и длина волны связаны соотношением ν =с/ λ, поэтому формулу (2.16) можно переписать в виде: Разность длин волн λ – λ0 является очень малой величиной, поэтому комптоновское изменение длины волны излучения заметно лишь при малых абсолютных значениях длины волны, то есть эффект наблюдается только для рентгеновского или гамма-излучения. Длина волны рассеянного фотона, как показывает эксперимент, не зависит от химического состава вещества, она определяется только углом θ, на который рассеивается фотон. Это легко объяснить, если учесть, что рассеяние фотонов происходит не на ядрах, а на электронах, которые в любом веществе идентичны. Величина h/mc в формуле (2.17) называется комптоновской длиной волны и для электрона равна λc = 2.43·10–12м. Теория атома Бора Со времен Древней Греции вплоть до конца XIX в. считалось, что все тела состоят из мельчайших частиц – атомов, которые являются неделимыми частицами материи, «кирпичиками мироздания». Всякое проявление существования материи сводилось к механическому перемещению этих частиц. О том, что атомы являются сложными частицами материи, первым догадался только Д. И. Менделеев. По его мнению, атомы были неделимы лишь известными в то время химическими методами. К концу XIX в. были установлены некоторые свойства атомов, свидетельствовавшие о том, что они имеют сложный состав. Было обнаружено, что в электрическом разряде в газе возникают так называемые катодные лучи, представляющие собой потоки отрицательно заряженных частиц, названных электронами. Установлено, что электроны вырываются из атомов, которые при этом становятся положительно заряженными ионами. Стало очевидным, что атомы являются сложной системой, в которой частицы, несущие отрицательный заряд, имеют одинаковую природу для всех атомов. В тоже время положительный заряд связан с основной массой атома, но ничего не было известно о том, как этот заряд распределяется внутри атома. В 1903 г. Д. Д. Томсон предложил первую модель, согласно которой атом представляет собой сферу, заполненную положительно заряженной материей, в которой взвешены отрицательно заряженные корпускулы – электроны. Томсон рассчитал размер такого шарика исходя из соображений, что электрон внутри сферы-атома совершает колебания с частотой, определяемой его удаленностью от центра сферы. Полученное таким образом значение радиуса атома (≈ 3·10–8 см) совпадало по порядку величины с газокинетическими размерами. Это совпадение являлось весомым доказательством справедливости модели, но как позже выяснилось, было случайным. Главное, чего не могла объяснить теория Томсона, это наличия в спектре излучения атомов множества линий. Ведь если электрон один (как в атоме водорода), то и линия должна быть одна, длина волны этой линии должна соответствовать частоте колебания электрона в атоме. Эксперимент же показал, что линий в спектре атома гораздо больше, чем электронов в его составе. К тому моменту уже было известно, что все атомы при определенных условиях испускают волны, частоты которых подчиняются определенным правилам. Для каждого атома набор линий является исключительно индивидуальным, как отпечатки пальцев для человека. Получить спектр атома, иона или молекулы можно с помощью прибора, снабженного устройством, разделяющим излучение на монохроматические составляющие (кварцевая или стеклянная призма, дифракционная решетка). Кроме того, необходимо заставить частицу излучать, т.е. перевести вещество в возбужденное состояние. Это может наблюдаться при различных видах электрического разряда через исследуемое вещество (гейслерова трубка, искра, дуговой разряд), при бомбардировке атомов газа электронами, испущенными накаленным катодом, при нагревании паров и газов (например, в пламени горелки), при освещении паров светом подходящей длины волны и т.д. Способ возбуждения подбирают исходя из свойств конкретного вещества. Так для наблюдения спектра атомов йода достаточно нагреть над пламенем запаянную кювету с кристаллическим йодом. Получение спектров золота или свинца (или еще более тяжелых элементов) уже требует помещения исследуемого вещества в дуговой разряд, происходящий в промежутке между электродами. Наиболее простой вид имеют спектры атома водорода и водородоподобных ионов, а также других изолированных атомов. Электроны, входящие в их состав, находятся под действием внутриатомных сил и не испытывают воздействия со стороны окружающих атомов. Спектры излучения этих частиц представляют собой несколько серий дискретных линий разной интенсивности. Такой спектр называют линейчатым. По мере перехода от более длинных волн к более коротким уровни постепенно сгущаются. С помощью стеклянной призмы глаз человека увидит только несколько линий одной из серий спектра атома водорода (рис. 3.1): λ = 656 нм (красный цвет), λ = 486 нм (зелено-голубой цвет) λ = 434 нм (сине-фиолетовый цвет) и λ = 410 нм (темно-фиолетовый цвет) Поэтому свечение возбужденного водорода имеет розоватую окраску (смесь указанных цветов).
Рис. 3.1. Видимая часть спектра атома водорода
Рис. 3.2. Видимая часть спектра атома железа Уединённый атом имеет бесконечно много уровней. В реальной среде различные взаимодействия с соседними частицами приводят к тому, что у атома остаётся только конечное число нижних уровней. Например, в условиях звёздных атмосфер в спектре атома водорода обычно различают 20 – 30 линий, но в разреженном межзвёздном газе могут наблюдаться сотни уровней, но не более тысячи. Число линий в спектре атома железа даже в земных условиях составляет несколько тысяч (рис. 3.2). Некоторое время ученые пытались как-то систематизировать линии в спектрах атомов. Первым успеха добился швейцарский физик Бальмер. Изучая спектр атома водорода в 1885 г. он обнаружил, что длины волн линий из серии, располагающейся в видимом диапазоне, удивительно точно описываются формулой: где λ0 – константа, n – целое число, принимающее значения 3, 4, 5 и т.д. Если длину волны выразить через частоту, получится формула:
где R = 3,29·1015 с–1 – постоянная Ридберга. Формула (3.1’) называется формулой Бальмера, а соответствующая серия спектральных линий – серией Бальмера. Исследования показали, что другие серии линий, лежащие в далекой ультрафиолетовой, а также в инфракрасной областях спектра, также подчиняются аналогичным формулам: в ультрафиолетовой области – серия Лаймана:
в инфракрасной области – серия Пашена:
серия Брэкета:
серия Пфунда:
и т.д.
Рис. 3.3. Энергетические состояния атома и серии спектральных линий Все серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:
где т задает номер серии и имеет для данной серии постоянное значение: m = 1, 2, 3,..., п может принимать значения m + 1, m + 2,... и определяет отдельные линии в серии. Первая линия в серии, которой соответствует самая большая длина волны, называется головной линией – в серии Бальмера спектра атома водорода это красная линия (рис. 3.1). При возрастании n частота линии в каждой серии стремится к предельному значению Линейчатый вид имеют спектры и других атомов. Однако количество линий в спектрах этих атомов значительно больше и взаимное расположение гораздо сложнее. Итак, характер излучения атомов свидетельствует об их достаточно сложном строении. В 1903 г. Ленард, изучая прохождение быстрых электронов через металлическую фольгу, пришел к выводу, что атом имеет «ажурное» строение, то есть заряд никак не может быть равномерно распределен по объему атома. Стоит добавить, что в то время еще не был открыт электрон как частица, поэтому выводы Ленарда сводились к тому, что через «непрозрачное окно», коим являлась фольга, проникает что-то, несущее отрицательный заряд. Этот факт казался на том момент удивительным. В 1913 г. Эрнест Резерфорд предпринял попытку прозондировать атом изнутри. В качестве зонда он использовал α -частицы, выделяющиеся при радиоактивном распаде сложных атомов.
Рис. 3.4. Опыт Резерфорда Оказалось, что при прохождении α -частиц через слой какого-либо вещества (например, через фольгу из золота) наблюдается изменение направления их движения (рассеяние). Отклонившуюся частицу можно зарегистрировать с помощью экрана, покрытого веществом, которое при попадании в него α -частицы, откликается вспышкой света.
Рис. 3.5. Резерфордовское рассеяние На рис. 3.5 показана траектория отклонения α -частицы при попадании в кулоновское поле ядра. Резерфорд показал, что угол отклонения α -частицы зависит от величины так называемого прицельного параметра b. Можно рассчитать минимальный прицельный параметр b, при котором частица отклонится от прямолинейной траектории, то есть ощутит действие поля ядра:
где b - прицельный параме
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.019 с.) |

 (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.16)
(1.16)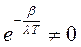 , то из равенства нулю выражения в скобках получаем:
, то из равенства нулю выражения в скобках получаем: или
или  (1.17)
(1.17)

 (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20)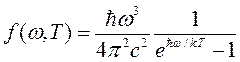 (1.21)
(1.21) (1.22)
(1.22)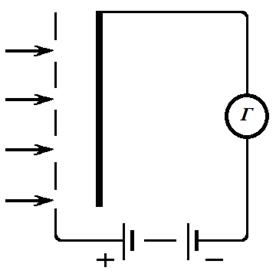

 (2.1)
(2.1)
 (2.2)
(2.2) (2.3)
(2.3)
 (2.8)
(2.8)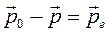 (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11)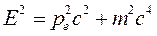 (2.12)
(2.12)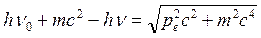 (2.13)
(2.13)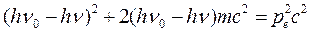 (2.14)
(2.14) (2.15)
(2.15)


 (2.16)
(2.16)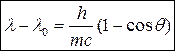 (2.17)
(2.17)

 (3.1)
(3.1) (3.1’)
(3.1’) (n = 2, 3, 4,...);
(n = 2, 3, 4,...); (n = 4, 5, 6,...),
(n = 4, 5, 6,...), (n = 5, 6, 7,...),
(n = 5, 6, 7,...), (n = 6, 7, 8,...),
(n = 6, 7, 8,...),
 (3.2)
(3.2) , которое называется границей серии.
, которое называется границей серии.

 (3.3)
(3.3)


