
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловое излучение. Квантовая оптикаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА
Тепловое излучение Излучение телами электромагнитных волн может осуществляться за счет различных видов энергии. Самым распространенным является тепловое излучение, т. е. испускание электромагнитных волн за счет внутренней энергии тела. Все остальные виды излучения, объединяются под общим названием «люминесценция». Тепловое излучение имеет место при любой температуре, однако при невысоких температурах излучаются практически лишь электромагнитные волны инфракрасного диапазона. Окружим излучающее тело оболочкой, внутренняя поверхность которого отражает все падающее на нее излучение. Воздух из оболочки удален. Отраженное оболочкой излучение частично или полностью поглощается телом. Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Равновесное состояние системы «тело – излучение» соответствует условию, когда распределение энергии между телом и излучением остается неизменным для каждой длины волны. Такое излучение принято называть равновесным излучением. Экспериментальные исследования показывают, что единственным видом излучения, которое может находиться в равновесии с излучающими телами, является тепловое излучение. Все остальные виды излучения оказываются неравновесными. Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при повышении температуры. Предположим, что равновесие между телом и излучением нарушено и тело излучает энергию большую, чем поглощает. Тогда внутренняя энергия тела будет убывать, что приведет к уменьшению температуры. Это, в свою очередь, приведет к уменьшению излучаемой телом энергии. Если равновесие нарушится в другую сторону, т. е. излучаемой энергии окажется меньше, чем поглощаемой, температура тела будет возрастать до тех пор, пока снова не установится равновесие. Из всех видов излучения равновесным может быть только тепловое излучение. К равновесным состояниям и процессам применимы законы термодинамики. Поэтому тепловое излучение подчиняется общим закономерностям, вытекающим из принципов термодинамики. К рассмотрению этих закономерностей мы и перейдем.
Формула Планка В 1900 г. немецкому физику Максу Планку удалось найти вид функции
где n – частота излучения; h – коэффициент пропорциональности, получивший название постоянной Планка, h = 6.625 × 10-34 Дж × с;
Плотность распределения радиационных осцилляторов была подсчитана Планком классически. Согласно распределению Больцмана, число частиц Nn, энергия каждой из которых равна e n, определяется формулой
где А – нормировочный множитель; k – постоянная Больцмана. Используя определение среднего значения дискретных величин, получаем выражение для средней энергии частиц, которое равно отношению полной энергии частиц к полному числу частиц:
где
Последующие преобразования приводят к соотношению
Таким образом, функция Кирхгофа, с учетом (3.4), имеет вид
Формула (4.3) называется формулой Планка. Эта формула согласуется с экспериментальными данными во всем интервале частот от 0 до
Опыт Боте. Фотоны Чтобы объяснить распределение энергии в спектре равновесного теплового излучения, достаточно, как показал Планк, допустить, что свет испускается квантами. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Эйнштейн выдвинул гипотезу, что свет и распространяется в виде дискретных частиц, названных первоначально световыми квантами. Впоследствии эти частицы получили название фотонов (1926 г.). Гипотезу Эйнштейна непосредственно подтвердил опыт Боте (рис. 6.1).
Вследствие малой интенсивности первичного пучка количество квантов, испускаемых фольгой, было невелико. При попадании в счетчик рентгеновских лучей запускался особый механизм (М), делавший отметку на движущейся ленте (Л). Если бы излучаемая энергия распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были бы срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении. Так было доказано существование особых световых частиц – фотонов. Энергия фотона определяется его частотой
Электромагнитная волна, как известно, обладает импульсом. Соответственно, и фотон должен обладать импульсом (p). Из соотношения (6.1) и общих принципов относительности вытекает, что
Такое соотношение между импульсом и энергией возможно только для частиц с нулевой массой покоя, движущихся со скоростью света. Таким образом: 1) масса покоя фотона равна нулю; 2) фотон движется со скоростью света. Сказанное означает, что фотон представляет собой частицу особого рода, отличную от таких частиц, как электрон, протон и т. п., которые могут существовать, двигаясь со скоростями, меньшими с, и даже покоясь. Выразив в (6.2) частоту w через длину волны l, получим:
где
Пусть на полностью поглощающую свет поверхность падает поток фотонов, летящих по нормали к поверхности. Если концентрация фотонов равна N, то на единицу поверхности падает в единицу времени Nc фотонов. При поглощении каждый фотон сообщает стенке импульс р = Е / с. Импульс, сообщаемый в единицу времени единице поверхности, т. е. давление Р света на стенку
Произведение NЕ равно энергии фотонов, заключенных в единице объема, т. е. плотности электромагнитной энергии w. Таким образом, давление, оказываемое светом на поглощающую поверхность, равно объемной плотности электромагнитной энергии P = w. При отражении от зеркальной поверхности фотон сообщает ей импульс 2 р. Поэтому для абсолютно отражающей поверхности P = 2 w.
Эффект Комптона Импульс фотона слишком мал и не поддается прямому измерению. Однако при столкновении фотона со свободным электроном величину передаваемого импульса уже можно измерить. Процесс рассеяния фотона на свободном электроне называется эффектом Комптона. Выведем соотношение, связывающее длину волны рассеянного фотона с углом рассеяния и длиной волны фотона до соударения. Пусть фотон с импульсом р и энергией Е = pc сталкивается с неподвижным электроном, энергия которого
Рис. 8.1 Импульс электрона отдачи будет равен Согласно закону сохранения энергии
Запишем закон сохранения импульса:
Возведем (8.2) в квадрат:
Учитывая, что релятивистская энергия
Переходя к длинам волн p =
или окончательно:
Величина В своем опыте Комптон использовал рентгеновское излучение с известной длиной волны и обнаружил, что у рассеянных фотонов длина волны увеличивается. На рис. 8.1 приведены результаты экспериментального исследования рассеяния монохроматического рентгеновского излучения на графите. Первая кривая (Q = 0°) характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния Q, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс длина волны. На всех графиках присутствует несмещенный компонент излучения (левый пик). Его наличие объясняется рассеянием первичного излучения на связанных электронах атома. Эффект Комптона и внешний фотоэффект подтвердили гипотезу о квантовой природе света, т. е. свет действительно ведет себя так, как если бы он состоял из частиц, энергия которых h n и импульс h /l. Вместе с тем, явления интерференции и дифракции света могут быть объяснены с позиции волновой природы. Оба эти подхода в настоящий момент представляются взаимодополняющими друг друга.
Принцип неопределенности В классической механике состояние материальной точки определяется заданием значений координат и импульса. Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных при измерениях получаются определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты х и компоненты импульса
Из (11.1) следует, что, чем меньше неопределенность одной из переменных (х или Соотношение, аналогичное (11.1), имеет место для у и
Соотношение (11.2) называется принципом неопределенности для величин А и В. Это соотношение сформулировал В. Гейзенберг в 1927 г. Утверждение о том, что произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка, называется принципом неопределенности. Энергия и время также являются канонически сопряженными величинами
Это соотношение означает, что определение энергии с точностью D Е должно занять интервал времени, равный по меньшей мере Соотношение неопределенности можно проиллюстрировать следующим примером. Попытаемся определить значение координаты х свободно летящей микрочастицы, поставив на ее пути щель шириной D х, расположенную перпендикулярно к направлению движения частицы. До прохождения частицы через щель ее составляющая импульса
Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной D х, соответствует угол j, для которого
Следовательно,
Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (11.1) вместо
Очевидно, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью применимо понятие траектории. Уже для макрочастицы размером 1 мкм неопределенности значений х и Принцип неопределенности является одним из фундаментальных положений квантовой механики.
Уравнение Шредингера В развитие идеи де-Бройля о волновых свойствах вещества австрийский физик Э. Шредингер получил в 1926 г. уравнение, названное впоследствии его именем. В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как законы Ньютона в классической механике и уравнения Максвелла в классической теории электромагнетизма. Оно позволяет найти вид волновой функции частиц, движущихся в различных силовых полях. Вид волновой функции или Y-функции получается из решения уравнения, которое выглядит следующим образом
Здесь m – масса частицы; i – мнимая единица; D – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам
Буквой U в уравнении (12.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других уравнений. Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера состоит из двух множителей, один из которых зависит только от координат, другой – только от времени
Здесь Е – полная энергия частицы, которая в случае стационарного поля остается постоянной;
В результате получим
Уравнение (12.3) называется уравнением Шредингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением и для краткости будем называть его просто уравнением Шредингера. Уравнение (12.3) часто записывают в виде
В квантовой механике большую роль играет понятие оператора. Под оператором подразумевается правило, посредством которого одной функции, обозначим ее
здесь
В этом уравнении символом
Оператор
где
или в векторном виде В разд. 10 мы уже обсуждали физический смысл Y-функции: квадрат модуля Y -функции (волновой функции) определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:
Поскольку квадрат модуля волновой функции равен произведению волновой функции на комплексно сопряженную величину
Тогда вероятность обнаружения частицы в объеме V
Для одномерного случая
Интеграл от выражения (12.5), взятый по всему пространству от
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна 1. В квантовой механике принимается, что волновая функция допускает умножение на отличное от нуля произвольное комплексное число С, причем
Условие (12.6) называется условием нормировки. Функции, удовлетворяющие этому условию, называются нормированными. В дальнейшем мы всегда будем полагать, что рассматриваемые нами Y-функции являются нормированными. В случае стационарного силового поля справедливо соотношение
т. е. плотность вероятности волновой функции равна плотности вероятности координатной части волновой функции и от времени не зависит. Свойства Y -функции: она должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек) и иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий. В уравнение Шредингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида
Частица в потенциальной яме Найдем собственные значения энергии и соответствующие им собственные волновые функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис. 13.1, а). Предположим, что частица
Рис. 13.1 может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U = 0 внутри ямы (при 0 £ х £ l) и Рассмотрим стационарное уравнение Шредингера. Поскольку Y-функция зависит только от координаты х, то уравнение имеет вид
За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Следовательно, и функция y за пределами ямы равна нулю. Из условия непрерывности следует, что y должна быть равна нулю и на границах ямы, т. е.
Этому условию должны удовлетворять решения уравнения (13.1). В области II (0 £ х £ l), где U = 0 уравнение (13.1) имеет вид
Используя обозначение
Решение такого уравнения имеет вид
Условию (14.2) можно удовлетворить соответствующим выбором постоянных k и a. Из равенства Далее из равенства
n = 0 исключено, поскольку при этом Из (13.4) получаем
Таким образом получаем, что энергия частицы в потенциальной яме может принимать только дискретные значения. На рис.13.1, б изображена схема энергетических уровней частицы в потенциальной яме. На этом примере реализуется общее правило квантовой механики: если частица локализована в ограниченной области пространства, то спектр значений энергии частицы дискретен, при отсутствии локализации спектр энергии непрерывен. Подставим значения k из условия (13.4) в (13.3) и получим
Для нахождения константы а воспользуемся условием нормировки, которое в данном случае имеет вид
На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение
Графики собственных значений функций при различных n изображены на рис. 13.2. На этом же рисунке показана плотность вероятности yy* обнаружения частицы на различных расстояниях от стенок ямы.
Рис. 13.2 Графики показывают, что в состоянии с n = 2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, несовместимо с представлением о траектории. Отметим, что, согласно классическим представлениям, все положения частицы в яме равновероятны.
Движение свободной частицы Рассмотрим движение свободной частицы. Полная энергия Е движущейся частицы равна кинетической энергии (потенциальная энергия U = 0). Уравнение Шредингера для стационарного состояния (12.3) имеет в этом случае решение
Полные (зависящие от времени) волновые функции таких стационарных состояний имеют вид
Это уравнение представляет собой суперпозицию двух плоских монохроматических волн равной частоты
Каждая такая функция – плоская волна описывает состояние, в котором частица обладает определенными значениями энергии Е и импульса р =
задает поведение свободной частицы. Таким образом, свободная частица в квантовой механике описывается плоской монохроматической волной де‑Бройля с волновым числом
Вероятность обнаружить частицу в любой точке пространства найдем как
т. е. вероятность обнаружить частицу вдоль оси х везде постоянна. Таким образом, если импульс частицы имеет определенное значение, то она, в соответствии с принципом неопределенности, с равной вероятностью может находиться в любой точке пространства. Иначе говоря, если импульс частицы точно известен, мы ничего не знаем о ее местонахождении. В процессе измерения координаты частица локализуется измерительным прибором, поэтому область определения волновой функции (17.1) для свободной частицы ограничивается отрезком
Гармонический осциллятор В заключение рассмотрим задачу о колебаниях квантового гармонического осциллятора. Таким осциллятором являются частицы, совершающие малые колебания около положения равновесия. На рис. 18.1, а изображен классический гармонический осциллятор в виде шарика массой m, подвешенного на пружине с коэффициентом жесткости k. Сила, действующая на шарик и ответственная за его колебания, связана с координатой х формулой
Уравнение Шредингера для гармонического осциллятора имеет вид
Решение этого уравнения приводит к квантованию энергии осциллятора. Собственные значения энергии осциллятора определяются выражением
Как и в случае потенциальной ямы с бесконечно высокими стенками, минимальная энергия осциллятора
При передаче энергии через фотон его частота оказывается равной w. Приведем (без вывода) выражения для нескольких первых собственных функций гармонического осциллятора:
Графики для соответствующих плотностей вероятности изображены на рис. 18.2. Границы «классической» траектории осциллятора помечены как
Рис. 18.2 Проведем сравнение с классическим случаем. Очевидно, что в этом случае вероятность График «классической» плотности вероятности изображен на рис. 18.3 пунктирной кривой. Видно, что, как и в случае потенциальной ямы, поведение квантового осциллятора существенным образом отличается от поведения классического.
На примере квантового осциллятора опять прослеживается упоминавшийся ранее принцип соответствия. На рис. 18.3 изображены графики для классической и квантовой плотностей вероятности при большом квантовом числе n. Хорошо видно, что усреднение квантовой кривой приводит к классическому результату.
Содержание ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА 1. Тепловое излучение..................................................................................... 3 2. Закон Кирхгофа. Абсолютно черное тело............................................. 4 3. Закон Стефана – Больцмана и закон Вина. Формула Рэлея – Джинса. 6 4. Формула Планка..................................................................................... 8 5. Явление внешнего фотоэффекта............................................................ 10 6. Опыт Боте. Фотоны............................................................................... 12 7. Излучение Вавилова – Черенкова........................................................ 14 8. Эффект Комптона.................................................................................. 17 ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ 9. Гипотеза де-Бройля. Опыт Дэвиссона и Джермера............................. 19 10. Вероятностный характер волн де-Бройля. Волновая функция......... 21 11. Принцип неопределенности................................................................ 24 12. Уравнение Шредингера....................................................................... 26 13. Част
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 971; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.011 с.) |

 , в точности соответствующий опытным данным. Для этого ему пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно, допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), пропорциональных частоте излучения:
, в точности соответствующий опытным данным. Для этого ему пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно, допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), пропорциональных частоте излучения: ,
,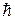 = h /2p =
= h /2p = , то его энергия e n должна быть кратной этой величине:
, то его энергия e n должна быть кратной этой величине: (4.1)
(4.1)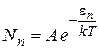 , n = 1, 2, 3… (4.2)
, n = 1, 2, 3… (4.2)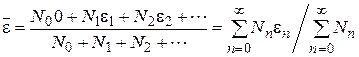 ,
,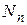 число частиц, обладающих энергией
число частиц, обладающих энергией  . С учетом (4.1) и (4.2) выражение для среднего значения энергии частиц имеет вид
. С учетом (4.1) и (4.2) выражение для среднего значения энергии частиц имеет вид .
.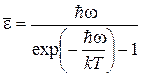 .
. . (4.3)
. (4.3) . В области малых частот, согласно правилам приближенных вычислений, при (
. В области малых частот, согласно правилам приближенных вычислений, при ( ):
):  »
»  и
и  выражение (4.3) преобразуется в формулу Рэлея – Джинса.
выражение (4.3) преобразуется в формулу Рэлея – Джинса. Тонкая металлическая фольга (Ф) помещалась между двумя газоразрядными счетчиками (Сч). Фольга освещалась пучком рентгеновских лучей с небольшой интенсивностью, под действием которых она сама становилась источником рентгеновских лучей.
Тонкая металлическая фольга (Ф) помещалась между двумя газоразрядными счетчиками (Сч). Фольга освещалась пучком рентгеновских лучей с небольшой интенсивностью, под действием которых она сама становилась источником рентгеновских лучей. . (6.1)
. (6.1)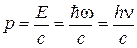 . (6.2)
. (6.2) ,
, – модуль волнового вектора k. Фотон летит в направлении распространения электромагнитной волны. Поэтому направления импульса р и волнового вектора k совпадают:
– модуль волнового вектора k. Фотон летит в направлении распространения электромагнитной волны. Поэтому направления импульса р и волнового вектора k совпадают: .
.
 .
. . После соударения импульс фотона равен
. После соударения импульс фотона равен  и направлен под углом Q, как показано на рис. 8.1.
и направлен под углом Q, как показано на рис. 8.1.
 , и полная релятивистская энергия
, и полная релятивистская энергия 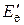 . Здесь мы используем релятивистскую механику, поскольку скорость электрона может достигать значений, близких к скорости света.
. Здесь мы используем релятивистскую механику, поскольку скорость электрона может достигать значений, близких к скорости света. или
или  , преобразуется к виду
, преобразуется к виду . (8.1)
. (8.1) .(8.2)
.(8.2) и вычтем это выражение из (8.1):
и вычтем это выражение из (8.1):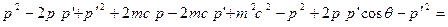
 . (8.3)
. (8.3)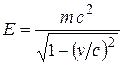 , можно показать, что правая часть выражения (8.2) равна
, можно показать, что правая часть выражения (8.2) равна  . Тогда после преобразования импульс фотона равен
. Тогда после преобразования импульс фотона равен .
. = h /l, Dl = l - l¢, получаем:
= h /l, Dl = l - l¢, получаем: ,
, . (8.4)
. (8.4) называется комптоновской длиной волны. Для электрона комптоновская длина волны l c = 0.00243 нм.
называется комптоновской длиной волны. Для электрона комптоновская длина волны l c = 0.00243 нм. . Неопределенности значений х и
. Неопределенности значений х и  . (11.1)
. (11.1) , z и
, z и  , а также для ряда других пар величин (такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать
, а также для ряда других пар величин (такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать . (11.2)
. (11.2) .
. .
. , зато координата х частицы является совершенно неопределенной (рис. 11.1).
, зато координата х частицы является совершенно неопределенной (рис. 11.1). В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность D х, но это достигается ценой утраты определенности значения
В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность D х, но это достигается ценой утраты определенности значения 
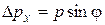 .
. .
.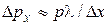 , и получаем
, и получаем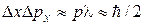 .
. , получим соотношение
, получим соотношение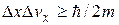 .
.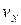 оказываются за пределами точности измерения этих величин, так что ее движение будет практически неотличимо от движения по траектории.
оказываются за пределами точности измерения этих величин, так что ее движение будет практически неотличимо от движения по траектории.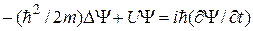 .
.  .
. . (12.2)
. (12.2) – координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1):
– координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1): .
.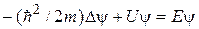 . (12.3)
. (12.3)
 .
. сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом
сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом ,
, – символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например
– символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например  и т. д.). В формуле (12.1) роль
и т. д.). В формуле (12.1) роль  , а роль f – правая часть формулы. Например, символ D означает двукратное дифференцирование по трем координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной функции
, а роль f – правая часть формулы. Например, символ D означает двукратное дифференцирование по трем координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной функции  на некоторую функцию U. Тогда
на некоторую функцию U. Тогда  , следовательно,
, следовательно,  . Если рассматривать функцию U в уравнении (12.3) как оператор, действие которого на Y-функцию сводится к умножению
. Если рассматривать функцию U в уравнении (12.3) как оператор, действие которого на Y-функцию сводится к умножению  . (12.4)
. (12.4)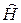 обозначен оператор, равный сумме операторов
обозначен оператор, равный сумме операторов  и U:
и U: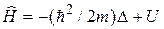 .
.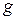 составляется уравнение, аналогичное (12.4). Оно имеет вид
составляется уравнение, аналогичное (12.4). Оно имеет вид ,
, – оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями
– оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями ;
;  ;
; 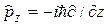 ,
,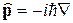 , где Ñ – градиент.
, где Ñ – градиент. , (12.5)
, (12.5)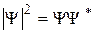 , то
, то .
. .
. .
. до
до  , равняется единице:
, равняется единице:
 и С Y описывают одно и то же состояние частицы. Это позволяет выбрать волновую функцию так, чтобы она удовлетворяла условию
и С Y описывают одно и то же состояние частицы. Это позволяет выбрать волновую функцию так, чтобы она удовлетворяла условию (12.6)
(12.6) ,
,
 вне ямы (при х < 0 и х > l).
вне ямы (при х < 0 и х > l). . (13.1)
. (13.1) . (13.2)
. (13.2) .
. , придем к известному из теории колебаний волновому уравнению
, придем к известному из теории колебаний волновому уравнению .
. . (13.3)
. (13.3) получаем
получаем 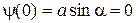 Þ a = 0.
Þ a = 0.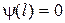 получаем
получаем  . Это условие выполняется при
. Это условие выполняется при (n = 1, 2, 3,...), (13.4)
(n = 1, 2, 3,...), (13.4) (n = 1, 2, 3,...), следовательно,
(n = 1, 2, 3,...), следовательно,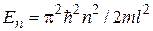 (n = 1, 2, 3,...).
(n = 1, 2, 3,...). .
. .
.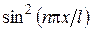 (равное, как известно, 1/2) на длину промежутка. Таким образом, получаем
(равное, как известно, 1/2) на длину промежутка. Таким образом, получаем 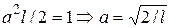 . Окончательно собственные волновые функции имеют вид
. Окончательно собственные волновые функции имеют вид (n = 1, 2, 3,...).
(n = 1, 2, 3,...).
 .
.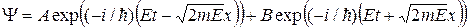 .
.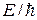 , распространяющихся одна в положительном направлении оси х с амплитудой А, а другая в противоположном, с амплитудой В. Но в неограниченном пространстве отраженной волны быть не должно, поэтому можно принять В = 0, и тогда
, распространяющихся одна в положительном направлении оси х с амплитудой А, а другая в противоположном, с амплитудой В. Но в неограниченном пространстве отраженной волны быть не должно, поэтому можно принять В = 0, и тогда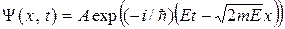 . (17.1)
. (17.1)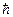 k. Реальная часть (17.1)
k. Реальная часть (17.1)
 .
. ,
, х. Плоскую волну уже нельзя считать монохроматической, имеющей одно определенное значение длины волны (импульса).
х. Плоскую волну уже нельзя считать монохроматической, имеющей одно определенное значение длины волны (импульса).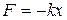 . Потенциальная энергия шарика есть
. Потенциальная энергия шарика есть
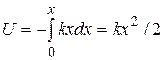 .
.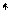 Если шарик вывести из положения равновесия, то он совершает колебания с частотой
Если шарик вывести из положения равновесия, то он совершает колебания с частотой  . Зависимость потенциальной энергии от координаты х показана на рис. 18.1, б.
. Зависимость потенциальной энергии от координаты х показана на рис. 18.1, б.

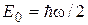 отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора
отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора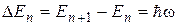 .
.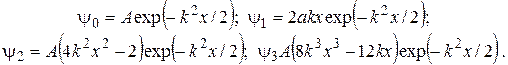
 и
и  .
.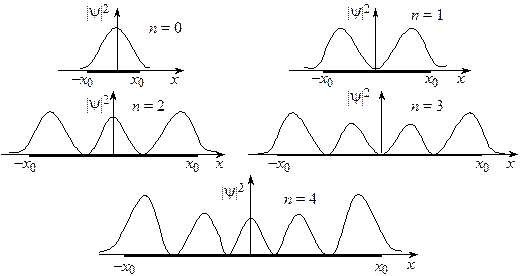
 нахождения частицы в интервале
нахождения частицы в интервале  обратно пропорциональна скорости частицы
обратно пропорциональна скорости частицы 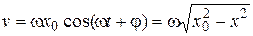 , где
, где  .
. Вероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных Y-функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.
Вероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных Y-функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.



