
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип соответствия в квантовой механикеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Критерий, при выполнении которого классическая физика дает достаточную точность и необязательно применять формулы квантовой механики, может быть записан в виде
где L – размеры системы, в которой движется частица; l – длина волны де‑Бройля. Смысл его заключается в том, что при длинах волн, много меньших размеров системы, квантово-механические особенности в поведении частиц оказываются несущественными. Продемонстрируем это утверждение на примере частицы в потенциальной яме (см. разд. 13). Y-функцию частицы (13.5), учитывая, что
Такое представление позволяет говорить о двух движущихся навстречу друг другу волнах де-Бройля. Сравнивая (15.1) с выражением для одномерной волны де-Бройля (9.2), получим выражение для импульса частицы для каждой из этих волн
и для длины волны де-Бройля:
Очевидно, что при n ® ¥, l ® 0 и поведение частицы должно быть близким к классическому. Проследим, как это отразится на спектре энергии частицы и ее волновых функциях. Оценим расстояния между соседними уровнями энергии частицы:
Относительное расстояние между уровнями
При n ® ¥ спектр энергии частицы получается почти непрерывным. Посмотрим теперь, как ведет себя плотность вероятности для частицы при больших n. Для классической частицы плотность вероятности постоянна и равна
Поведение плотности вероятности при больших n показано на рис. 15.1 (n = 10). Видно, что значение Таким образом, по мере возрастания n частица все более утрачивает квантовые свойства, и при больших значениях n квантовая физика переходит в классическую. Полученный результат является частным случаем общего физического принципа – принципа соответствия: любая новая теория, претендующая на большую общность, чем классическая теория, обязательно должна переходить в старую, классическую теорию в тех случаях, в которых последняя была построена и многократно проверена экспериментально.
16. Прохождение частицы
Пусть частица, движущаяся слева направо, встречает на своем пути потенциальный барьер высотой
Совершенно иначе выглядит поведение частицы согласно квантово-механическому описанию. Даже при Рассмотрим случай
Для области II (
Положим, что решение уравнения (16.1) имеет следующий вид:
Тогда подстановка этой функции в уравнение (16.1) приводит к характеристическому уравнению
где Общее решение уравнения (16.1) имеет следующий вид: ● для области I:
● для области III:
Решив подстановкой Заметим, что решение вида В области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент
Из этих условий вытекают соотношения
Разделим все уравнения (17.3) на
Количественно эффект туннелирования можно оценить, вычислив плотность вероятности
В случае пренебрежения отраженными волнами на границах I – II и II – III, отношение квадратов модулей амплитуд отраженной и падающей волн определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения:
Отношение квадратов модулей амплитуд прошедшей и падающей волн определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности):
Коэффициенты отражения и прозрачности связаны соотношением
В результате решения системы уравнений (16.4), получается
Значение
Отношение
Из полученного выражения следует, что вероятность прохождения частицы через потенциальный барьер зависит от ширины барьера l и от разности энергий ( Если при какой-либо ширине барьера коэффициент прохождения D равен 0,01, то при увеличении ширины в два раза D станет равным 0,012 = 0,0001, т. е. уменьшится в 100 раз. Тот же эффект вызвало бы возрастание в четыре раза значения (
Рис. 16.2 На рис. 16.2 изображены: в области I – действительная часть падающей волны ( В случае потенциального барьера произвольной формы (рис. 16.3) коэффициент прозрачности определяется более общей формулой
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем рассмотренное нами явление называют туннельным эффектом. На основе этого эффекта построены многие современные приборы, например туннельные диоды и транзисторы. Рассмотрим случай, когда
для области II
Общие решения уравнений (16.5) и (16.6) имеют следующий вид: ● для области I
● для области II
где Заметим, что, как и в случае высокого потенциального барьера, решение вида В области II имеется только волна, прошедшая над барьером и распространяющаяся слева направо. Поэтому коэффициент
В области II
При
Рис. 16.5 Используя стандартные условия (16.7), можно показать, что коэффициент отражения
Движение свободной частицы Рассмотрим движение свободной частицы. Полная энергия Е движущейся частицы равна кинетической энергии (потенциальная энергия U = 0). Уравнение Шредингера для стационарного состояния (12.3) имеет в этом случае решение
Полные (зависящие от времени) волновые функции таких стационарных состояний имеют вид
Это уравнение представляет собой суперпозицию двух плоских монохроматических волн равной частоты
Каждая такая функция – плоская волна описывает состояние, в котором частица обладает определенными значениями энергии Е и импульса р =
задает поведение свободной частицы. Таким образом, свободная частица в квантовой механике описывается плоской монохроматической волной де‑Бройля с волновым числом
Вероятность обнаружить частицу в любой точке пространства найдем как
т. е. вероятность обнаружить частицу вдоль оси х везде постоянна. Таким образом, если импульс частицы имеет определенное значение, то она, в соответствии с принципом неопределенности, с равной вероятностью может находиться в любой точке пространства. Иначе говоря, если импульс частицы точно известен, мы ничего не знаем о ее местонахождении. В процессе измерения координаты частица локализуется измерительным прибором, поэтому область определения волновой функции (17.1) для свободной частицы ограничивается отрезком
Гармонический осциллятор В заключение рассмотрим задачу о колебаниях квантового гармонического осциллятора. Таким осциллятором являются частицы, совершающие малые колебания около положения равновесия. На рис. 18.1, а изображен классический гармонический осциллятор в виде шарика массой m, подвешенного на пружине с коэффициентом жесткости k. Сила, действующая на шарик и ответственная за его колебания, связана с координатой х формулой
Уравнение Шредингера для гармонического осциллятора имеет вид
Решение этого уравнения приводит к квантованию энергии осциллятора. Собственные значения энергии осциллятора определяются выражением
Как и в случае потенциальной ямы с бесконечно высокими стенками, минимальная энергия осциллятора
При передаче энергии через фотон его частота оказывается равной w. Приведем (без вывода) выражения для нескольких первых собственных функций гармонического осциллятора:
Графики для соответствующих плотностей вероятности изображены на рис. 18.2. Границы «классической» траектории осциллятора помечены как
Рис. 18.2 Проведем сравнение с классическим случаем. Очевидно, что в этом случае вероятность График «классической» плотности вероятности изображен на рис. 18.3 пунктирной кривой. Видно, что, как и в случае потенциальной ямы, поведение квантового осциллятора существенным образом отличается от поведения классического.
На примере квантового осциллятора опять прослеживается упоминавшийся ранее принцип соответствия. На рис. 18.3 изображены графики для классической и квантовой плотностей вероятности при большом квантовом числе n. Хорошо видно, что усреднение квантовой кривой приводит к классическому результату.
Содержание ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА 1. Тепловое излучение..................................................................................... 3 2. Закон Кирхгофа. Абсолютно черное тело............................................. 4 3. Закон Стефана – Больцмана и закон Вина. Формула Рэлея – Джинса. 6 4. Формула Планка..................................................................................... 8 5. Явление внешнего фотоэффекта............................................................ 10 6. Опыт Боте. Фотоны............................................................................... 12 7. Излучение Вавилова – Черенкова........................................................ 14 8. Эффект Комптона.................................................................................. 17 ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ 9. Гипотеза де-Бройля. Опыт Дэвиссона и Джермера............................. 19 10. Вероятностный характер волн де-Бройля. Волновая функция......... 21
11. Принцип неопределенности................................................................ 24 12. Уравнение Шредингера....................................................................... 26 13. Частица в потенциальной яме............................................................. 30 14. Потенциальная яма конечной глубины.............................................. 32 15. Принцип соответствия в квантовой механике.................................... 35 16. Прохождение частицы через потенциальный барьер. Туннельный эффект......................................................................................................... 36 17. Движение свободной частицы............................................................. 42 18. Гармонический осциллятор................................................................ 43 Малышев Михаил Николаевич, Павловская Мария Владимировна, Попов Юрий Игоревич, Земцов Антон Валерьянович Основы квантовой физики Учебное пособие Редактор Н. В. Рощина ЛР № 020617 от 24.06.98.
Подписано в печать 00.09.2003. Формат 60´84 1/16. Бумага офсетная. Печать офсетная. Гарнитура «Times». Усл. печ. л. 2,79. Уч.-изд. л. 3,0. Тираж 200 экз. Заказ Издательство СПбГЭТУ «ЛЭТИ»
[1] Прямоугольный барьер называется высоким, если энергия частицы Е меньше высоты U 0потенциального барьера, в противном случае барьер называется низким.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.95.173 (0.01 с.) |

 ,
,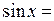
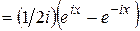 , можно записать в виде
, можно записать в виде . (15.1)
. (15.1)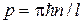
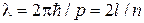 .
.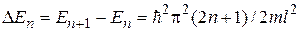 .
. .
. (15.2)
(15.2) Плотность вероятности (15.2) постоянна и удовлетворяет условию нормировки
Плотность вероятности (15.2) постоянна и удовлетворяет условию нормировки .
. колеблется около среднего значения 1/ l. Физический смысл в этом случае имеет лишь среднее значение плотности вероятности. Поэтому при n >> 1
колеблется около среднего значения 1/ l. Физический смысл в этом случае имеет лишь среднее значение плотности вероятности. Поэтому при n >> 1  , т. е. квантовая вероятность переходит в классическую.
, т. е. квантовая вероятность переходит в классическую. и шириной l (рис. 16.1).
и шириной l (рис. 16.1). По классическим представлениям, поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера (
По классическим представлениям, поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера ( ), то частица беспрепятственно проходит над барьером и на участке 0 £ х £ l лишь уменьшается скорость частицы. Затем при х > l скорость принимает первоначальное значение. Если же
), то частица беспрепятственно проходит над барьером и на участке 0 £ х £ l лишь уменьшается скорость частицы. Затем при х > l скорость принимает первоначальное значение. Если же  , то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
, то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может. . (16.1)
. (16.1) и
и 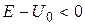 ) уравнение имеет вид
) уравнение имеет вид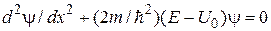 . (16.2)
. (16.2) .
. ,
,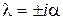 и
и  .
. ;
; .
. , где
, где  .
.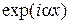 соответствует волне, распространяющейся в положительном направлении оси х, а решение вида
соответствует волне, распространяющейся в положительном направлении оси х, а решение вида  волне, распространяющейся в противоположном направлении.
волне, распространяющейся в противоположном направлении. в выражении для
в выражении для 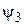 следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся стандартными условиями, которым должна удовлетворять Y‑функция,
следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся стандартными условиями, которым должна удовлетворять Y‑функция,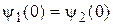 и
и  ;
;
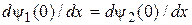 и
и  .
.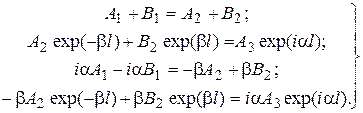 ; (16.3)
; (16.3) и введем обозначения
и введем обозначения  ,
,  ,
,  ,
,  и
и  . Тогда уравнения (16.3) примут вид
. Тогда уравнения (16.3) примут вид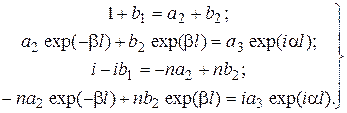 ; (16.4)
; (16.4)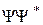 обнаружения частицы в каждой из областей пространства. Оценим степень прозрачности потенциального барьера.
обнаружения частицы в каждой из областей пространства. Оценим степень прозрачности потенциального барьера. .
. .
. .
.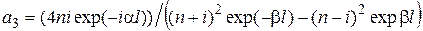 .
.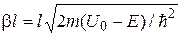 обычно бывает больше единицы, поэтому, учитывая, что
обычно бывает больше единицы, поэтому, учитывая, что  , получим
, получим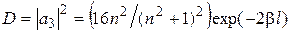 .
. имеет значение порядка единицы. Поэтому окончательно можно считать, что
имеет значение порядка единицы. Поэтому окончательно можно считать, что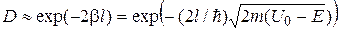 .
. ).
).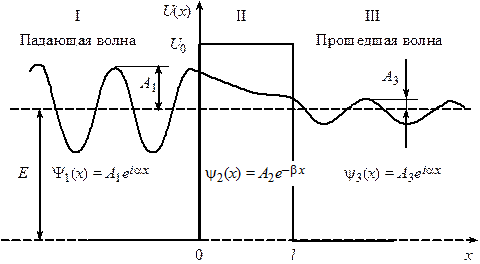
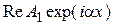 ); в области II – экспоненциально убывающая Y‑функция (
); в области II – экспоненциально убывающая Y‑функция ( ) и в области III – действительная часть прошедшей волны (
) и в области III – действительная часть прошедшей волны (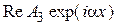 ). Построение выполнено при условии пренебрежения отраженными волнами на границах I – II и II – III, при этом
). Построение выполнено при условии пренебрежения отраженными волнами на границах I – II и II – III, при этом  и
и  .
. ).
).
 (рис. 16.4). Для области I уравнение Шредингера имеет вид
(рис. 16.4). Для области I уравнение Шредингера имеет вид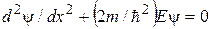 ,(16.5)
,(16.5)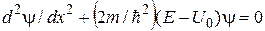 . (16.6)
. (16.6) ,
, и
и 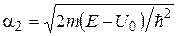 .
.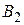 в выражении для
в выражении для 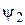 следует принять равным нулю. Для нахождения остальных коэффициентов можно воспользоваться стандартными условиями, которым должна удовлетворять функция
следует принять равным нулю. Для нахождения остальных коэффициентов можно воспользоваться стандартными условиями, которым должна удовлетворять функция  :
: ) представляет собой косинусоиду с волновым числом
) представляет собой косинусоиду с волновым числом длина волны (волновое число
длина волны (волновое число 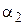 ) действительной части Y‑функции в области II совпадает с длиной волны действительной части волновой функции в области I. С ростом
) действительной части Y‑функции в области II совпадает с длиной волны действительной части волновой функции в области I. С ростом  действительная часть волновой функции в области II перестает быть гармонической. На рис. 16.5 изображены действительная часть падающей волны (
действительная часть волновой функции в области II перестает быть гармонической. На рис. 16.5 изображены действительная часть падающей волны (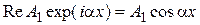 ) и действительная часть прошедшей волны (
) и действительная часть прошедшей волны ( ).
).
 и коэффициент прохождения
и коэффициент прохождения  для низкого (
для низкого ( ;
;  .
. .
. . Следовательно,
. Следовательно,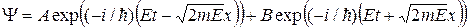 .
.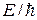 , распространяющихся одна в положительном направлении оси х с амплитудой А, а другая в противоположном, с амплитудой В. Но в неограниченном пространстве отраженной волны быть не должно, поэтому можно принять В = 0, и тогда
, распространяющихся одна в положительном направлении оси х с амплитудой А, а другая в противоположном, с амплитудой В. Но в неограниченном пространстве отраженной волны быть не должно, поэтому можно принять В = 0, и тогда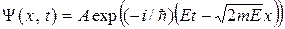 . (17.1)
. (17.1)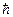 k. Реальная часть (17.1)
k. Реальная часть (17.1)
 .
. ,
, х. Плоскую волну уже нельзя считать монохроматической, имеющей одно определенное значение длины волны (импульса).
х. Плоскую волну уже нельзя считать монохроматической, имеющей одно определенное значение длины волны (импульса).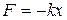 . Потенциальная энергия шарика есть
. Потенциальная энергия шарика есть
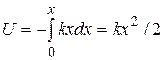 .
.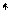 Если шарик вывести из положения равновесия, то он совершает колебания с частотой
Если шарик вывести из положения равновесия, то он совершает колебания с частотой  . Зависимость потенциальной энергии от координаты х показана на рис. 18.1, б.
. Зависимость потенциальной энергии от координаты х показана на рис. 18.1, б.

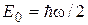 отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора
отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора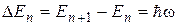 .
.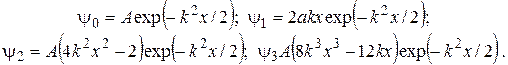
 и
и  .
.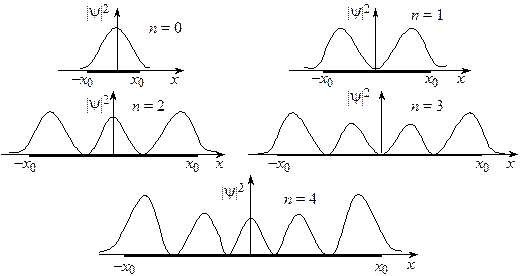
 нахождения частицы в интервале
нахождения частицы в интервале  обратно пропорциональна скорости частицы
обратно пропорциональна скорости частицы 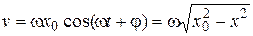 , где
, где  .
. Вероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных Y-функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.
Вероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных Y-функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.


 197376, С.-Петербург, ул. Проф. Попова, 5
197376, С.-Петербург, ул. Проф. Попова, 5


