
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовая теория и статистическая физикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Квантовая теория и статистическая физика (Часть I) Квантовая механика Конспект лекций для студентов ЭКТ-2 Г. Оглавление §1. Экспериментальные основы квантовой механики.. 3 §2. Классическое и квантовое описание системы.. 4 §3. Принцип неопределенности.. 5 §4.Полный набор динамических переменных. 5 §5. Постулаты квантовой механики.. 5 §6. Роль классической механики в квантовой механике. 6 §7.Волновая функция и ее свойства. 6 §8. Принцип суперпозиции состояний.. 6 §9. Понятие о теории представлений.. 7 §10.Операторы в квантовой механике. 7 §11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра. 8 §12. Среднее значение измеряемой величины.. 11 §13. Вероятность результатов измерения. 11 §14. Коммутативность операторов и одновременная измеримость физических величин (1/2*) 12 §15. Операторы координаты §16. Решение задачи на собственные функции и собственные значения для оператора §17. Решение задачи на собственные функции и собственные значения для оператора §18. Вычисление коммутаторов, содержащих операторы §19 Волновое уравнение. 18 § 20 Производная оператора по времени.. 19 § 21 Интегралы движения в квантовой механике. 20 §22. Флуктуации физических величин (1/2*) 20 § 23. Неравенства Гайзенберга. (1/2*) 22 § 24.Оператор Гамильтона различных систем.. 23 § 25. Стационарное состояние различных систем.. 25 § 26. Решение волнового уравнения в случае свободной материальной точки.. 25 § 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы.. 27 § 28. Собственный механический момент (спин) 28 § 29*. Операторы § 30. Спиновая переменная волновой функции.. 29 § 31. Матрицы Паули (и их свойства)*. 30 § 32. Принцип тождественности.. 32 §33. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения. 32 A.1. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение. 36 A.2. Критерий применимости теории возмущений.. 37 A.3. Стационарная теория возмущений в случае близких энергетических уровней. 38 Экзаменационные вопросы по курсу "Квантовая теория". 41 Экзаменационные задачи по курсу "Квантовая теория". 42 Экзаменационные вопросы по курсу "Квантовая теория".(минимум) 43 Экзаменационные задачи по курсу "Квантовая теория".(минимум) 43 Решения задач по курсу "Квантовая теория". 44
Экспериментальные основы квантовой механики 1900г. Планк ввел понятие о квантах и ввел квантовую постоянную. Работа Планка объясняла теорию излучения твердых тел. 1905г. Классификация спектров Ритцем и Ридбергом. Все спектральные линии могут быть посчитаны через термы 1913г. Н. Бор теоретически объяснил спектр атома водорода (постулаты Бора). Эксперименты Франка и Герца. Они рассматривали неупругое рассеяние электронов на атомах. Пропускали пучки электронов через пары ртути. При определенных энергиях, электроны при соударении с атомами ртути теряли часть своей энергии.
Установка:
Была показана энергетическая дискретность атома ртути, определены энергетические уровни:
1922г. Опыты Штерна и Герлаха по расщеплению атомного пучка в неоднородном магнитном поле.
По оси z поле в обкладках магнита неоднородно. Так как есть градиент поля
Наблюдалось расщепление атомного пучка. С точки зрения классической теории все Подтвердили, что магнитный момент атома квантуется, т. е. принимает дискретные значения.
где
1923 – 1924 гг. Теория Де Бройля корпускулярно-волнового дуализма частиц. Соотношения теории:
Здесь слева параметры частицы: энергия и импульс. Справа параметры волны: частота, волновой вектор.
Волна Де Бройля:
1927г. Дэвиссон и Джермер. Рассеяние электронов на кристаллической решетке. Подтверждение волновых свойств частиц. Транспонированный оператор
Отметим следующие свойства: 1)
Из выражения (10.1) получаем:
2)
3)
Сумма операторов:
Произведение операторов:
В общем случае
Коммутатор Если Если Так как физические величины вещественны, то число операторов в квантовой механике ограничено. Собственные значения эрмитовых операторов вещественны, значит только их можно ставить в соответствие физическим величинам. Запишем определение среднего:
Так как результаты измерений вещественны, то
тогда
т.е.
Обозначим
Тогда из (10.2) получаем
Из (10.3) имеем для любых
где [§11.] Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра Начнем с дискретного спектра, т.к. ему соответствует квадратично-интегрируемые функции. Задача на собственные функции и собственные значения для дискретного спектра:
Так как
Так как
Умножая (11.1) скалярно на
Теперь (11.2) умножаем справа на
Почленно из (11.3) вычтем (11.4):
т.к.
Рассмотрим случай невырожденного спектра. Спектр вырожденный, если одному собственному значению соответствует несколько собственных функций. Например:
Невырожденный спектр – все собственные значения различные. 1) Рассмотрим (11.6) при 2) Теперь пусть Тогда случаи 1 и 2 дают условие ортонормированности:
Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему функций, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функциям эрмитового оператора как по базису. Запишем это разложение:
где индекс i пробегает по всем значениям, удовлетворяющим задаче (11.1). Формулу (11.7) следует отличать от принципа суперпозиции
где Найдем коэффициенты Применяя условие ортонормированности, получим:
Тогда из (11.7) получаем
Далее
Из (11.7/) также можно получить еще одно соотношение:
(*) Теперь рассмотрим случай непрерывного спектра.
У собственной функции индексом является собственное значение. Собственные значения непрерывны, они сплошь заполняют соответствующую числовую ось. В этом случае собственные функции не нормируемы (квадратично не интегрируемы). Используем искусственную операцию – введем понятие собственных дифференциалов, по формуле:
т. е. на числовой оси рассмотрим функции с равным весом на интервале Условие ортонормируемости: Здесь
Собственные функции
По аналогии с дискретным спектром:
Принцип тождественности Этот принцип в квантовой механике определенным образом связан с принципом Гайзенберга. Если рассмотрим ансамбль одинаковых частиц, то идентификация этих частиц невозможна. Одинаковые частицы обладают всеми одинаковыми внутренними свойствами (m, e, s, …). Так как в квантовой механике не существует понятия «траектория», то невозможно различить одинаковые частицы. Например, в электронном газе существуют не отдельные частицы, а их ансамбль. В такой системе имеет место тождественность частиц. Итак: в ансамбле одинаковых частиц реализуются состояния, инвариантные относительно их перестановок. Т. к. такие частицы идентифицировать невозможно, то не различимы и состояния, полученные перестановкой частиц.
Квантовая теория и статистическая физика (Часть I) Квантовая механика Конспект лекций для студентов ЭКТ-2 Г. Оглавление §1. Экспериментальные основы квантовой механики.. 3 §2. Классическое и квантовое описание системы.. 4 §3. Принцип неопределенности.. 5 §4.Полный набор динамических переменных. 5 §5. Постулаты квантовой механики.. 5 §6. Роль классической механики в квантовой механике. 6 §7.Волновая функция и ее свойства. 6 §8. Принцип суперпозиции состояний.. 6 §9. Понятие о теории представлений.. 7 §10.Операторы в квантовой механике. 7 §11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра. 8 §12. Среднее значение измеряемой величины.. 11 §13. Вероятность результатов измерения. 11 §14. Коммутативность операторов и одновременная измеримость физических величин (1/2*) 12 §15. Операторы координаты §16. Решение задачи на собственные функции и собственные значения для оператора §17. Решение задачи на собственные функции и собственные значения для оператора §18. Вычисление коммутаторов, содержащих операторы §19 Волновое уравнение. 18 § 20 Производная оператора по времени.. 19 § 21 Интегралы движения в квантовой механике. 20 §22. Флуктуации физических величин (1/2*) 20 § 23. Неравенства Гайзенберга. (1/2*) 22 § 24.Оператор Гамильтона различных систем.. 23 § 25. Стационарное состояние различных систем.. 25 § 26. Решение волнового уравнения в случае свободной материальной точки.. 25 § 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы.. 27 § 28. Собственный механический момент (спин) 28 § 29*. Операторы § 30. Спиновая переменная волновой функции.. 29 § 31. Матрицы Паули (и их свойства)*. 30 § 32. Принцип тождественности.. 32 §33. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения. 32 A.1. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение. 36 A.2. Критерий применимости теории возмущений.. 37 A.3. Стационарная теория возмущений в случае близких энергетических уровней. 38 Экзаменационные вопросы по курсу "Квантовая теория". 41 Экзаменационные задачи по курсу "Квантовая теория". 42 Экзаменационные вопросы по курсу "Квантовая теория".(минимум) 43 Экзаменационные задачи по курсу "Квантовая теория".(минимум) 43 Решения задач по курсу "Квантовая теория". 44
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.50 (0.01 с.) |

 , импульса
, импульса  , момента импульса
, момента импульса  , энергии
, энергии  . 13
. 13 . 15
. 15 (и
(и 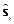 и
и  и их свойства. 29
и их свойства. 29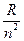 , где
, где  - постоянная Ридберга, n – натуральное число.
- постоянная Ридберга, n – натуральное число.
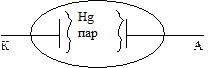

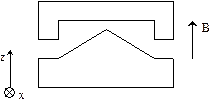
 , то если пропускать вдоль оси x частицы, имеющие магнитный момент
, то если пропускать вдоль оси x частицы, имеющие магнитный момент  , то возникает сила:
, то возникает сила: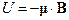

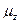 равновероятны и поэтому должна получиться одна широкая полоса. Наблюдались две четкие линии.
равновероятны и поэтому должна получиться одна широкая полоса. Наблюдались две четкие линии. ,
,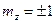 для серебра.
для серебра.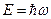



 ,
,  - длина волны Де Бройля.
- длина волны Де Бройля.

 (10.1)
(10.1)
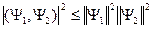
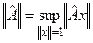
 . Это операторное равенство предполагает
. Это операторное равенство предполагает
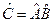 , тогда
, тогда 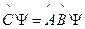 . Это операторное равенство предполагает
. Это операторное равенство предполагает
 не коммутативны
не коммутативны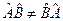

 , то операторы
, то операторы  и
и 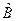 называются коммутативными (операторы
называются коммутативными (операторы  , то операторы
, то операторы 
 тоже должно быть вещественным, т.е.
тоже должно быть вещественным, т.е. (10.2)
(10.2) ,
,
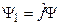 , тогда
, тогда
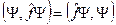 (10.3)
(10.3) :
: ,
,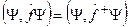 ,
,
 (сопряженный и транспонированный).
(сопряженный и транспонированный). (11.1)
(11.1) -собственные функции
-собственные функции - собственные значения
- собственные значения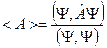 . Если речь идет о физической величине, то
. Если речь идет о физической величине, то  , где
, где 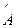 .
.

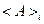 - это среднее значение величины
- это среднее значение величины  в i -ом квантовом состоянии. Так как среднее – вещественно, то и собственные значения вещественны. У эрмитового оператора
в i -ом квантовом состоянии. Так как среднее – вещественно, то и собственные значения вещественны. У эрмитового оператора 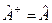 собственные значения вещественны
собственные значения вещественны  (все эрмитовы операторы имеют вещественные спектры).
(все эрмитовы операторы имеют вещественные спектры). (11.2)
(11.2)
 слева, получим
слева, получим (11.3)
(11.3)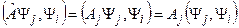 (11.4)
(11.4)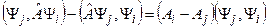 (11.5)
(11.5)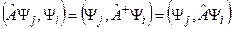 . Из (11.5) имеем
. Из (11.5) имеем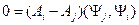 (11.6)
(11.6)
 , тогда
, тогда 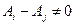 ,
,  .
.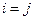 . В этом случае скалярное произведение
. В этом случае скалярное произведение  . Обычно вводят нормировку
. Обычно вводят нормировку  .
.
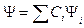 , (11.7)
, (11.7) ,
,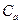 - вес состояния
- вес состояния  и суммирование ведется по произвольным a=1,…,k. Заметим, что если
и суммирование ведется по произвольным a=1,…,k. Заметим, что если  (модель Юнга с ширмой и электроном), то
(модель Юнга с ширмой и электроном), то 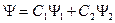 .
. из (11.7). Умножим скалярно (11.7) на
из (11.7). Умножим скалярно (11.7) на 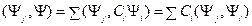
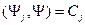
 ,
,  (11.7/)
(11.7/)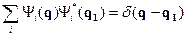
 - равенство Парсеваля (условие замкнутости).
- равенство Парсеваля (условие замкнутости).

 (11.8)
(11.8) . Собственные дифференциалы (11.8) квадратично-интегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.
. Собственные дифференциалы (11.8) квадратично-интегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций. .
. дает расходящийся интеграл, т. е. равен
дает расходящийся интеграл, т. е. равен  . Но для собственных дифференциалов имеем:
. Но для собственных дифференциалов имеем:
 обладают свойством полноты, т. е. они образуют базис, по которому может быть разложена любая функция:
обладают свойством полноты, т. е. они образуют базис, по которому может быть разложена любая функция: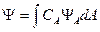 ,
, 

 - равенство Парсеваля
- равенство Парсеваля


