
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
A.3. Стационарная теория возмущений в случае близких энергетических уровней.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть у нас два близких уровня, а остальные уровни хорошо удовлетворяют критерию (5). Пусть близкие уровни - это уровни i=1,2. Близость уровней определяется из критерия (5). Модификация теории возмущений состоит в том, чтобы в качестве нулевого приближения для 1 и 2 состояния подобрать такие функции По определению:
Мы рассмотрим набор
Очевидно, что
Распишем:
Рассмотрим свойства невозмущенной функции: Они удовлетворяют ЗШЛ:
где
Эта матрица имеет диагональный вид, т. к. мы рассматриваем матричные элементы на собственных функциях этого оператора. Мы ввели
тогда (5) будет для Таким образом, мы ввели новый возмущенный базис Искомое преобразование является унитарным, так как оно не нарушает условия нормировки. Надо подобрать коэффициенты Используем
Но
или в матричном виде
Из свойства ортонормированности найдем свойства коэффициентов
т.е.
Это унитарное преобразование, оно сохраняет нормировку. Запишем ЗШЛ для модифицированных функций.
тогда подставим явно
Рассмотрим случай i=1, умножим левую и правую части этого уравнения скалярно на
Введем обозначения:
Перепишем эти уравнения в виде
Система линейных однородных уравнений. Она имеет нетривиальное решение только при det=0. Обозначим
Имеем решение
При i=2, то по аналогии
и обозначив
получаем
Во втором случае решение аналогично первому. Однако мы приписываем одному знак +, а другому -. Имеем тогда уровни энергии:
Перейдем к системе (7). Из нее имеем
Кроме этого используем соотношение
т.е. имеем нормировку
Рассмотрим i=j=1 (и аналогично i=j=2)
Введем обозначение:
где α и β – вспомогательные углы, определяемые через матричные элементы H 12, H 11 и H 22. Тогда коэффициенты b имеем в виде
Таким образом, при
Модификация касалась только этих дух близких состояний. Остальные состояния не модифицировались, т.к. они сразу удовлетворяли критерию. Теперь Экзаменационные вопросы по курсу "Квантовая теория".
Экзаменационные задачи по курсу "Квантовая теория". [Задача 1.] Найти оператор а) б) Задача 2. Показать, что произвольный линейный оператор
[Задача 3.] Найти Задача 4. Решить уравнение
Задача 5. Для стационарного состояния вида
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины а) б) [Задача 6.] В [Задача 7.] Рассчитать коммутатор Задача 8. Найти коммутатор Задача 9. Для стационарного состояния
рассчитать Экзаменационные вопросы по курсу "Квантовая теория".(минимум)
Экзаменационные задачи по курсу "Квантовая теория".(минимум)
Задача 1. Найти оператор а) б) Задача 2. Найти В сферических координатах Задача 3. В Задача 4. Рассчитать коммутатор Решения задач по курсу "Квантовая теория"
[Задача 1.] Найти оператор а) б) Решение. Подставляя явный вид а)
б)
Здесь использовано обращение функций
Задача 2. Показать, что произвольный линейный оператор
Решение. Легко видеть, что справедливо разложение
двух операторов, первый из которых является эрмитовым:
а второй – антиэрмитовым:
С их помощью будем иметь
Всякая линейная комбинация эрмитовых операторов с вещественными коэффициентами есть Эрмитов оператор. Произведение двух эрмитовых операторов не обязательно эрмитово.
[Задача 3.] Найти Решение. Из определения
Отсюда с учетом эрмитовости
Легко видеть, что в общем случае
Задача 4. Решить уравнение (7.3) для оператора
Решение. Из решения задачи 3(б) и равенств
найдем
т.е. рассматриваемый оператор
Решая его, найдем
Из условия периодичности (см. задачу 3(б))
вытекает равенство
из которого получаем ограничение
Из дискретности и невырожденности спектра следует, что после нормировки (8.4) функции Запишем условие нормировки (8.4) в виде
В общем случае постоянный множитель есть комплексное число, однако ввиду всегда допустимого введения произвольного фазового множителя
будем предполагать вещественность константы
Окончательно запишем
Задача 9. Для стационарного состояния вида
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины а) б) Решение. а) По определению запишем
Расчет числителя (12.3) дает
где использованы соотношения
Аналогичным образом для знаменателя (12.3) получим
Следовательно, для
б) Учитывая свойство (7.2) и определение (12.2), запишем
Расчет числителя (12.4) дает
таким образом, для
[Задача 6.] В Решение. В случае бесконечно глубокой ямы по определению имеем
Интересующее нас решение ищем на отрезке Поскольку в точках и
следуют соотношения
где
совпадающему с уравнением (13.1) или (13.2) (в зависимости от характера спектра), т.е. функция Таким образом, приходим к задаче
Отсюда следует:
Положительность собственного значения
Подстановка (17.8) в граничные условия (17.6) приводит к системе однородных уравнений
для неизвестных коэффициентов
дает условие квантования
собственного значения
где
Поскольку собственные функции оператора
Отсюда с учетом решения задачи 12 находим
Подставляя найденное значение константы в (17.10), запишем решение задачи в окончательной форме
[Задача 7.] Рассчитать коммутатор Решение. Для нахождения явного вида оператора
Задача 8. Найти коммутатор Решение. Используя (19.2) и вид
запишем
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.117.240 (0.008 с.) |

 и
и  , которые обращали бы в ноль
, которые обращали бы в ноль 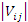 - числитель критерия (5).
- числитель критерия (5).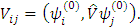


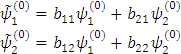

 - невозмущенный оператор.
- невозмущенный оператор.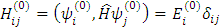 (6)
(6)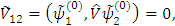
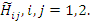

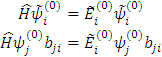
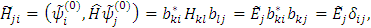
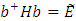

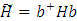





 и
и 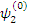 , тогда имеем:
, тогда имеем:


 (7)
(7)
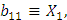







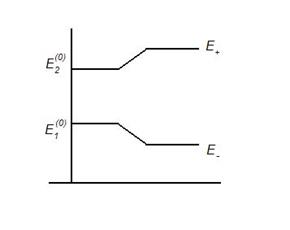






 теория возмущений срабатывает для двух близких уровней. Теперь в качестве нулевого приближения берут:
теория возмущений срабатывает для двух близких уровней. Теперь в качестве нулевого приближения берут:
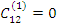 и
и  – теория возмущения работает.
– теория возмущения работает. , импульса
, импульса  , момента импульса
, момента импульса  , энергии
, энергии  .
.  .
. 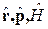 (и
(и  *).
*).  и
и  и их свойства.
и их свойства.  , если
, если ,
,  ;
;  ,
,  ;
; ,
, 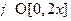 ;
;  ,
,  .
. может быть представлен в виде
может быть представлен в виде ;
;  ,
,  .
. , если
, если 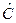 - произведение эрмитовых операторов
- произведение эрмитовых операторов  и
и 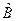
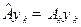 для оператора
для оператора ,
, 

 , рассчитать средние значения величин, соответствующих операторам:
, рассчитать средние значения величин, соответствующих операторам: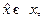
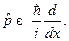
 - представлении (одномерная система) решить уравнение
- представлении (одномерная система) решить уравнение  в случае частицы в бесконечно глубокой потенциальной яме, ширины
в случае частицы в бесконечно глубокой потенциальной яме, ширины  .
. .
.

 и
и  .
. .
. и проводя интегрирование по частям, получим
и проводя интегрирование по частям, получим ,
,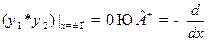
 ,
,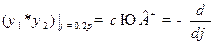 .
.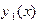 и
и  в нуль на бесконечности в случае (а) и условие периодичности функции
в нуль на бесконечности в случае (а) и условие периодичности функции  и
и  в случае (б). В обоих случаях оператор
в случае (б). В обоих случаях оператор 
 ,
,  ,
, .
. ,
,  ,
,  .
. ;
; ,
,  /
/ .
. .
.
 ,
, .
. .
.
 ,
, ;
; 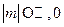
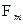 будут обладать свойством (8.3).
будут обладать свойством (8.3).
 ,
, 
 . Это дает
. Это дает
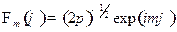 ;
;  ,
,



 будем иметь
будем иметь
 .
.

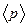 будем иметь
будем иметь
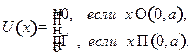

 и
и  потенциальная энергия частицы обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области (17.2) равна нулю. Оказавшись в области (17.2), частица все время будет находиться в ней. Из формул
потенциальная энергия частицы обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области (17.2) равна нулю. Оказавшись в области (17.2), частица все время будет находиться в ней. Из формул 


 - волновая функция
- волновая функция 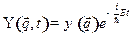 , удовлетворяющая стационарному уравнению Шредингера
, удовлетворяющая стационарному уравнению Шредингера
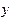 , удовлетворяющая (17.5), есть собственная функция
, удовлетворяющая (17.5), есть собственная функция  оператора
оператора  . Из сказанного вытекают граничные условия
. Из сказанного вытекают граничные условия  , накладываемые на решение уравнения (17.5).
, накладываемые на решение уравнения (17.5).

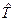 и
и  . Решение уравнения (17.7) представимо в виде суперпозиции двух элементарных состояний, которые на языке
. Решение уравнения (17.7) представимо в виде суперпозиции двух элементарных состояний, которые на языке  (17.3) интерпретируются как волны де Броля, распространяющиеся в противоположных направлениях оси
(17.3) интерпретируются как волны де Броля, распространяющиеся в противоположных направлениях оси  :
:

 . Критерий существования тривиального решения этой системы
. Критерий существования тривиального решения этой системы


 - пока неизвестная вещественная (в силу наличия у
- пока неизвестная вещественная (в силу наличия у  произвольного фазового множителя (10.1) это всегда возможно) константа, для функции (17.8) будем иметь
произвольного фазового множителя (10.1) это всегда возможно) константа, для функции (17.8) будем иметь


 .
. необходимо рассмотреть результат его действия на произвольную функцию
необходимо рассмотреть результат его действия на произвольную функцию  , запишем
, запишем
 .
. в
в 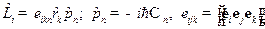 ,
, .
.


