
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое и квантовое описание системыСодержание книги
Поиск на нашем сайте
Опыт № 2. Заменяем Э1 на Э1/. Опыт № 3. Объединяем экраны Э1 и Э1/ При классическом описании опыт 3 давал бы сложение интенсивностей от опыта 1 и 2. Однако опыт 3 показал интерференционную картину, а это волновые свойства. Частица с определенной вероятностью проходит как через щель 1 так и через щель 2. Нельзя точно сказать через какую щель пройдет электрон. Классическая интерпретация (с числом степеней свободы n=1) решается составлением уравнений в форме Гамильтона:
Можно найти траекторию частицы. В общем случае состояние механической системы определяется
Скорость Координата Если известна точка [§3.] Принцип неопределенности Две формулировки: 1) В микромире понятие “траектория” отсутствует 2) Канонически сопряженные величины одновременно неизмеримы В трехмерном пространстве канонически сопряженные величины будут: px и x py и y pz и z Здесь n=3. Имеем 3 одновременно измеряемые динамические переменные. Например: 1) px. py. pz 2) x, y, z 3) x, y, pz и тд.
[§4.] Полный набор динамических переменных Полный набор динамических переменных – это наибольший набор независимых одновременно измеримых динамических переменных. Измерение полного набора динамических переменных полностью определяет состояние квантово-механической системы. Число динамических переменных в квантовой системе - n и по сравнению с классической системой (2n) уменьшается в 2 раза. Максимальный набор – это значит, что к этому набору не может быть добавлена ни одна другая переменная, которая не являлась бы их функцией. В этом случае они не зависимы. Каждая из этих переменных не является функцией другой переменной из этого же набора. Заметим, что здесь зависимость не линейная (как в линейной алгебре), а функциональная.
[§5.] Постулаты квантовой механики Часто выделяют 4 постулата: 1) Постулат о волновой функции. Каждой системе (состоянию кв.-мех. системы) может быть поставлена в соответствие волновая функция динамических переменных (из полного набора) и времени, полностью описывающей состояние системы. Динамические переменные одновременно измеримы. 2) О связи физических величин и объектов математики (операторов). Каждой физической величине (наблюдаемой) ставится в соответствие оператор: 3) Связь между результатами измерения физической величины Пусть
4) Определение среднего значения физической величины
Здесь введено понятие скалярного произведения для функций из гильбертова пространства. Гильбертово пространство – это пространство квадратично интегрируемых функций (нормируемых функций). Если
Это определение для
Это аналог длины в векторном пространстве.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.230.81 (0.01 с.) |

 Опыт № 1. Имеется источник частиц, экран с достаточно узким отверстием. Картину наблюдаем на Э2
Опыт № 1. Имеется источник частиц, экран с достаточно узким отверстием. Картину наблюдаем на Э2
 динамическими переменными, т.е.
динамическими переменными, т.е. 



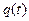 , то чтобы найти положение точки
, то чтобы найти положение точки  надо знать
надо знать  одновременно, т. е. координаты и импульс должны быть измерены одновременно. Если мы знаем
одновременно, т. е. координаты и импульс должны быть измерены одновременно. Если мы знаем  - n – мерный вектор динамических переменных; функция динамических переменных и времени
- n – мерный вектор динамических переменных; функция динамических переменных и времени  - описывает эволюцию квантово-механических систем. классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона. В квантово-механической системе описывается эволюция системы через
- описывает эволюцию квантово-механических систем. классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона. В квантово-механической системе описывается эволюция системы через  - функцию от n динамических переменных.
- функцию от n динамических переменных.
 и значением оператора
и значением оператора  (т. е. решением математических задач)
(т. е. решением математических задач) - значение физической величины
- значение физической величины 
 является одним из собственных значений оператора
является одним из собственных значений оператора  , соответствующие собственным значениям
, соответствующие собственным значениям 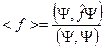
 - квадратично интегрируемые функции, тогда:
- квадратично интегрируемые функции, тогда:




