
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль классической механики в квантовой механикеСодержание книги
Поиск на нашем сайте
Два момента присутствия классической механики в квантовой механике: 1) Измерение микросистем (квантово-механических систем) проводятся с помощью классических приборов (систем). 2) Принцип соответствия – переход квантово-механических результатов в классическую механику (h à 0, можно ввести такую величину размерности действия A, что
[§7.] Волновая функция и ее свойства Волновая функция динамических переменных и времени определяет состояние системы с точностью до фазового множителя, т. е.
т. е.
[§8.] Принцип суперпозиции состояний Если мы имеем состояния системы, описываемые функциями
Отсюда получаем: уравнения, которым подчиняется функция
Понятие о теории представлений Представление – это совокупность переменных, в которых решается задача (т. е. набор динамических переменных). Рассмотрим одну материальную точку. Число степеней свободы n=3. Здесь могут быть 2 случая: 1) Под Оператор координаты Оператор импульса Здесь 2) Под Оператор координаты Оператор импульса Здесь Мы в основном будем использовать [§10.] Операторы в квантовой механике В силу принципа суперпозиции в квантовой механике используются линейные операторы. Задача на собственные функции и собственные значения:
Определение оператора:
Свойство линейности: Если
т.к. Сопряженный оператор – это оператор, который связан с данным оператором соотношением:
или
Тогда получаем:
Если Транспонированный оператор
Отметим следующие свойства: 1)
Из выражения (10.1) получаем:
2)
3)
Сумма операторов:
Произведение операторов:
В общем случае
Коммутатор Если Если Так как физические величины вещественны, то число операторов в квантовой механике ограничено. Собственные значения эрмитовых операторов вещественны, значит только их можно ставить в соответствие физическим величинам. Запишем определение среднего:
Так как результаты измерений вещественны, то
тогда
т.е.
Обозначим
Тогда из (10.2) получаем
Из (10.3) имеем для любых
где [§11.] Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра Начнем с дискретного спектра, т.к. ему соответствует квадратично-интегрируемые функции. Задача на собственные функции и собственные значения для дискретного спектра:
Так как
Так как
Умножая (11.1) скалярно на
Теперь (11.2) умножаем справа на
Почленно из (11.3) вычтем (11.4):
т.к.
Рассмотрим случай невырожденного спектра. Спектр вырожденный, если одному собственному значению соответствует несколько собственных функций. Например:
Невырожденный спектр – все собственные значения различные. 1) Рассмотрим (11.6) при 2) Теперь пусть Тогда случаи 1 и 2 дают условие ортонормированности:
Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему функций, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функциям эрмитового оператора как по базису. Запишем это разложение:
где индекс i пробегает по всем значениям, удовлетворяющим задаче (11.1). Формулу (11.7) следует отличать от принципа суперпозиции
где Найдем коэффициенты Применяя условие ортонормированности, получим:
Тогда из (11.7) получаем
Далее
Из (11.7/) также можно получить еще одно соотношение:
(*) Теперь рассмотрим случай непрерывного спектра.
У собственной функции индексом является собственное значение. Собственные значения непрерывны, они сплошь заполняют соответствующую числовую ось. В этом случае собственные функции не нормируемы (квадратично не интегрируемы). Используем искусственную операцию – введем понятие собственных дифференциалов, по формуле:
т. е. на числовой оси рассмотрим функции с равным весом на интервале Условие ортонормируемости: Здесь
Собственные функции
По аналогии с дискретным спектром:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.244 (0.007 с.) |

 ). По Эйнштейну этот переход характеризуется
). По Эйнштейну этот переход характеризуется  . Если
. Если  , то переход в классическую механику Ньютона.
, то переход в классическую механику Ньютона.
 и
и  описывает одно и тоже состояние, где
описывает одно и тоже состояние, где 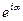 - фазовый множитель. Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки). Функции
- фазовый множитель. Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки). Функции 
 - элементарный объем
- элементарный объем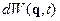 - вероятность того, что динамические переменные
- вероятность того, что динамические переменные  лежат в интервале
лежат в интервале  . Это определение справедливо для квадратично интегрируемых функций. Для не квадратично интегрируемых функций величина
. Это определение справедливо для квадратично интегрируемых функций. Для не квадратично интегрируемых функций величина  пропорциональна плотности вероятности.
пропорциональна плотности вероятности. , то суперпозиции этих функций также отвечает некоторое состояние этой системы:
, то суперпозиции этих функций также отвечает некоторое состояние этой системы:
 - имеем
- имеем 


 - имеем
- имеем 



 , то
, то
 , то
, то 
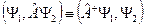


 - то оператор называется эрмитовым (самосопряженным).
- то оператор называется эрмитовым (самосопряженным).

 (10.1)
(10.1)
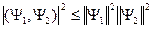
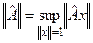
 . Это операторное равенство предполагает
. Это операторное равенство предполагает
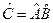 , тогда
, тогда 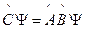 . Это операторное равенство предполагает
. Это операторное равенство предполагает
 не коммутативны
не коммутативны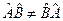

 , то операторы
, то операторы  и
и 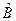 называются коммутативными (операторы
называются коммутативными (операторы  , то операторы
, то операторы 
 тоже должно быть вещественным, т.е.
тоже должно быть вещественным, т.е. (10.2)
(10.2) ,
,
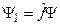 , тогда
, тогда
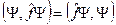 (10.3)
(10.3) ,
,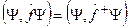 ,
,
 (сопряженный и транспонированный).
(сопряженный и транспонированный). (11.1)
(11.1) -собственные функции
-собственные функции - собственные значения
- собственные значения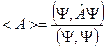 . Если речь идет о физической величине, то
. Если речь идет о физической величине, то  , где
, где 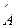 .
.

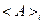 - это среднее значение величины
- это среднее значение величины  в i -ом квантовом состоянии. Так как среднее – вещественно, то и собственные значения вещественны. У эрмитового оператора
в i -ом квантовом состоянии. Так как среднее – вещественно, то и собственные значения вещественны. У эрмитового оператора 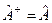 собственные значения вещественны
собственные значения вещественны  (все эрмитовы операторы имеют вещественные спектры).
(все эрмитовы операторы имеют вещественные спектры). (11.2)
(11.2)
 слева, получим
слева, получим (11.3)
(11.3)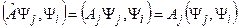 (11.4)
(11.4)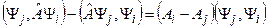 (11.5)
(11.5)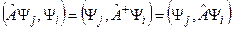 . Из (11.5) имеем
. Из (11.5) имеем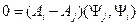 (11.6)
(11.6)
 , тогда
, тогда 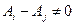 ,
,  .
.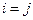 . В этом случае скалярное произведение
. В этом случае скалярное произведение  . Обычно вводят нормировку
. Обычно вводят нормировку  .
.
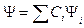 , (11.7)
, (11.7)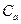 - вес состояния
- вес состояния  (модель Юнга с ширмой и электроном), то
(модель Юнга с ширмой и электроном), то 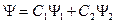 .
. из (11.7). Умножим скалярно (11.7) на
из (11.7). Умножим скалярно (11.7) на 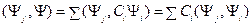
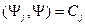
 ,
,  (11.7/)
(11.7/)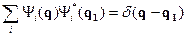
 - равенство Парсеваля (условие замкнутости).
- равенство Парсеваля (условие замкнутости).

 (11.8)
(11.8) . Собственные дифференциалы (11.8) квадратично-интегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.
. Собственные дифференциалы (11.8) квадратично-интегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций. .
. дает расходящийся интеграл, т. е. равен
дает расходящийся интеграл, т. е. равен  . Но для собственных дифференциалов имеем:
. Но для собственных дифференциалов имеем:
 обладают свойством полноты, т. е. они образуют базис, по которому может быть разложена любая функция:
обладают свойством полноты, т. е. они образуют базис, по которому может быть разложена любая функция: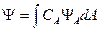 ,
, 

 - равенство Парсеваля
- равенство Парсеваля


