Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы движения в квантовой механикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В классической механике В квантовой механике, чтобы величина Для того чтобы физическая величина сохранялась, необходимо и достаточно, чтобы 1. т. к. 2. 3. 4. 5. §22. Флуктуации физических величин (1/2*)
Пусть есть
Мы вводили флуктуацию
отклонение величины
Перенесем все это на язык квантовой механики, т. к. физической величине Можно показать, что Неравенство Коши-Шварца: Оно справедливо и для функциональных пространств, в том числе и для гильбертова пространства, которое рассматривается в квантовой механике.
Для двух векторов оно имеет вид
имеет смысл тот, что
Теперь если обозначить
Теперь если определить
В случае квантовой механики
Задача. Для стационарного состояния частицы в бесконечно глубокой потенциальной яме найти Решение. Будем считать, что в.ф. для данной системы уже получены (см. §27). Согласно определению: Поэтому остается рассчитать а) В случае
Подставляя полученные значения в (22.1), получаем б)Для оператора Среднее значение будет равно
Подставим в (22.1) и получим
§ 23. Неравенства Гайзенберга. (1/2*) Канонически сопряженные величины одновременно неизмеримы – это принцип неопределенности. Под канонически сопряженными понимаем величины
В квантовой механике для операторов
Более того Это можно записать в виде Если (*) Вывод:
Обозначим Тогда из Введем обозначение
Подставим это в неравенство Коши-Шварца, тогда
Используем эрмитовость операторов
тогда
Поделим левую и правую части на
Используем определение среднего
тогда
Или
Операторы
Первое слагаемое обозначим Второе слагаемое Оператор Тогда
где
Окончательно
В полученном неравенстве математически заложен принцип неопределенности Гайзенберга. Если величина измерена точно, то Если Когда измеряем величину [§ 24.] Оператор Гамильтона различных систем Этот вопрос идентичен вопросу рассмотренному в классической механике - будут те же соотношения, но для операторов
Поставим в соответствие конкретной системе операторы В декартовой системе координат Здесь n – число точек в системе.
Мы рассматриваем
Мы рассматриваем декартову систему координат. Гамильтониан Перейдем к более простой задаче. Рассмотрим систему N материальных точек во внешнем стационарном поле
Здесь
Выражение, описывающее внешнее воздействие обладает аддитивностью, т. е.
Индекс a означает, что разные частицы могут взаимодействовать с внешним полем по разному закону. Если все частицы одинаковые и одинаково взаимодействуют с внешним полем, то индекс a убирается. Внутреннее взаимодействие Рассмотрим случай свободной материальной точки. Соответственно она ни с чем не взаимодействует:
Тогда
тогда Если материальная точка во внешнем поле:
Нестационарное поле Стационарное поле Центральное поле Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек. В случае классической механики: Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.
Зависимость энергии от модуля В квантовой механике в
где
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1057; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.247 (0.007 с.) |

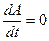 , где
, где 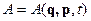 , тогда A – интеграл движения.
, тогда A – интеграл движения. , которой ставится в соответствие оператор
, которой ставится в соответствие оператор  , была интегралом движения нужно, чтобы
, была интегралом движения нужно, чтобы 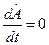 .
.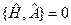 .
. , то
, то 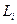 -значение момента импульса сохраняется, т. е. является интегралом движения.
-значение момента импульса сохраняется, т. е. является интегралом движения.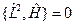 .
. 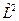 - интеграл движения.
- интеграл движения.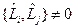 . Отсюда следует. Что различные компоненты момента импульса одновременно не измеримы. А измерима только одна проекция
. Отсюда следует. Что различные компоненты момента импульса одновременно не измеримы. А измерима только одна проекция  .
.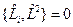 . Квадрат импульса одновременно измерим с любой компонентой момента импульса.
. Квадрат импульса одновременно измерим с любой компонентой момента импульса.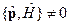 , тогда импульс не является интегралом движения.
, тогда импульс не является интегралом движения. - физическая величина, которая при измерении с вероятностью Wi дает величину
- физическая величина, которая при измерении с вероятностью Wi дает величину  , тогда мы можем говорить о среднем
, тогда мы можем говорить о среднем 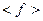 и о дисперсии
и о дисперсии 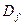 , где
, где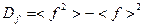 .
.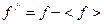 ,
,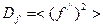
 .
.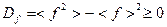 .
.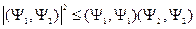
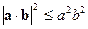
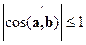 .
.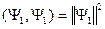 ,
, 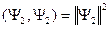 .
.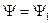 ,
, 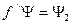 , тогда будем также рассматривать статистическое усреднение
, тогда будем также рассматривать статистическое усреднение 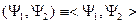 . Отсюда получим из неравенства Коши-Шварца:
. Отсюда получим из неравенства Коши-Шварца:
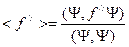 . К тому же по определению из
. К тому же по определению из 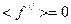 , тогда
, тогда 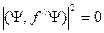 . Из этого следует, что
. Из этого следует, что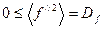 .
.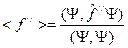 .
.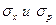
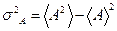 (22.1)
(22.1)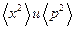
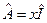 числа
числа 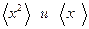 находится вычислениями
находится вычислениями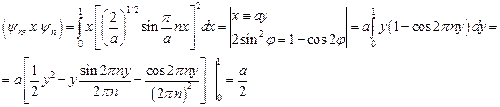
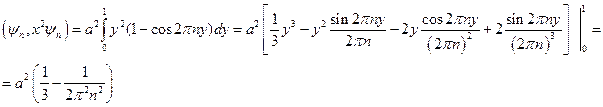
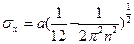

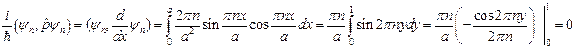
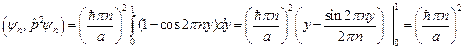
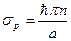
 и
и 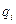 .
.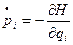

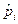 и
и 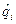 , которые поставлены в соответствие канонически сопряженным величинам имеем
, которые поставлены в соответствие канонически сопряженным величинам имеем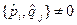 .
.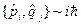 , а сам коммутатор
, а сам коммутатор 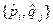 имеет вид оператора
имеет вид оператора 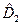 .
.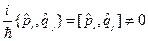 .
.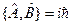 , то
, то 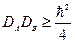 , тогда
, тогда 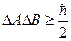 , где
, где 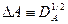 .
.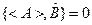
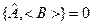 , т.к.
, т.к. 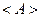 и
и 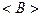 есть числа.
есть числа.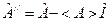 . Здесь
. Здесь 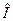 - единичный оператор.
- единичный оператор.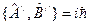 (*)
(*)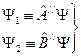
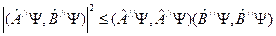
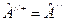 ,
,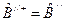 ,
,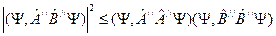 .
.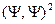 , тогда
, тогда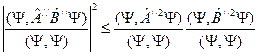
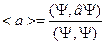 ,
,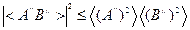 .
.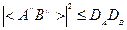
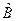 не коммутируют, тогда
не коммутируют, тогда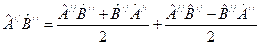 .
.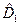 ,
, 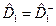 .
.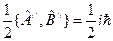 .
.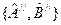 дает чисто мнимое число.
дает чисто мнимое число. ,
,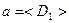 .
.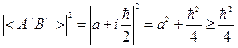 .
.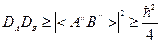 .
.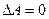 ,т.е.
,т.е. 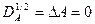 .
.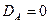 , но тогда для
, но тогда для 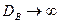 , т. к.
, т. к.  . Для того чтобы
. Для того чтобы 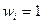 необходимо чтобы система находилась в состоянии
необходимо чтобы система находилась в состоянии 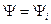 .
.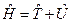 .
.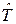 и
и 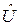 :
: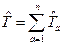 ,
, 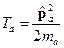 .
.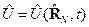 .
.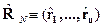 - функция от оператора координаты.
- функция от оператора координаты. - представление, здесь
- представление, здесь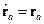
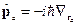
 мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).
мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).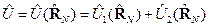
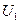 отвечает за внутреннее взаимодействие между частицами.
отвечает за внутреннее взаимодействие между частицами.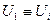

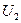 отвечает за внешнее воздействие на систему частиц.
отвечает за внешнее воздействие на систему частиц.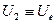 .
.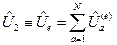 .
.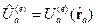
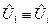 не аддитивно.
не аддитивно.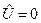
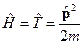 , или в
, или в  ,
,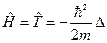 .
.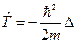 ,
,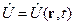 .
.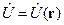 .
.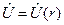 .
.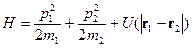 .
.
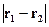 есть изотропность пространства.
есть изотропность пространства.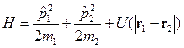 ,
,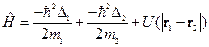 ,
,