
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекции 9,10. Элементы квантовой механикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Известны 4 механики: классическая или ньютоновская механика, релятивиская механика (теория относительности), квантовая механика и релятивиская квантовая механика. Первые две механики изучались в I - ой части курса физики, а сейчас переходим к изучению квантовой механики. Квантовая механика - это механика микромира, механика движения микрочастиц в микрополях - атомах, молекулах, кристаллах. Ее можно рассматривать как основную теорию атомных явлений. Опытные факты, на которых она основывается, отражают физические процессы, почти полностью лежащие за пределами непосредственного человеческого восприятия. Поэтому нет ничего удивительного в том, что теория содержит физические понятия, чуждые повседневному опыту. Начало создания последовательной теории атомных явлений можно отнести к 1924 г., когда Луи де Бройль предположил, что природа вещества также является двойственной (корпускулярной и волновой). 9.1. Гипотеза де Бройля. Опытное обоснование корпускулярно-волнового дуализма материи. Опыт Девиссона- Джермера В 1924 г. де Бройль выдвинул гипотезу (предположение), что дуализм (двойственность) не являются особенностью одних только оптических явлений (см. лекцию 8), а имеет универсальное значение, т.е. де Бройль выдвинул гипотезу о всеобщности корпускулярно-волнового дуализма. Согласно де Бройлю каждой частице, независимо от ее природы, следует поставить в соответствии волну, длина которой l связана с импульсом частицы соотношением (формула де Бройля)
а частота v=E/h или w=2pv=E / т.е. определяется энергией Е частицы. Найдем длину волны де Бройля, соответствующую движущемуся электрону. Кинетическая энергия, приобретенная электроном в ускоряющем поле равна
и скорость
Из (1) и (4) следует (учитывая, что е=1.6×10-19 Кл, m=9.1×10-31 кг, напряжение U выражается в вольтах )
В обычных электронных приборах используют напряжение 1¸10 4 В. Соответствующие длины волн летящих электронов составляют 10¸0.1 По гипотезе де Бройля не только фотоны [см.(8.4)], но и все "обыкновенные частицы" (электроны, протоны, нейтроны и др.) обладают волновыми свойствами, которые, в частности, должны проявляться в явлениях интерференции, дифракции. Гипотеза де Бройля вскоре была подтверждена экспериментально. Девиссон и Джермер в 1927 г. наблюдали дифракцию электронов на монокристалле никеля.
через гальванометр. Ожидали получить дифракционную картину, аналогичную картине возникающей при дифракции рентгеновских лучей на том же кристалле, поскольку длина волны де Бройля для электронов изменялась в диапазоне длин волн рентгеновских лучей. Ожидание подтвердилось. Согласно формуле Вульфа-Брегга [ см. лекции 4, 5 формула (13) ] условие дифракционного максимума имеет вид 2dsinq=ml, (6) где d - расстояние между атомными плоскостями, q - угол скольжения, m=1, 2, 3... Для никеля d=2.03
  себя как волны. Позднее были поставлены другие себя как волны. Позднее были поставлены другие
Заметим, что волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии с волнами в классической физике. т.е. они "не похожи ни на что из того, что вам когда-нибудь приходилось видеть" (Фейнман). В классической физике "понять" означало составить себе наглядный образ объекта или процесса. Квантовую физику нельзя понять в таком смысле слова и поэтому следует отказаться от попыток строить наглядные модели поведения квантовых объектов.
      До прохождения частицы через щель рх имеет До прохождения частицы через щель рх имеет
импульса Dрх=0, зато координата х частицы является
частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность Dх, но это достигается ценой утраты определенности значения рх. Действительно, вследствии дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах некоторого угла 2j, где j - угол, соответствующий первому дифракционному минимуму. Таким образом, появляется неопределенность импульса Dрх=рsinj. (8) Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной Dх соответствует угол j, для которого [ cм. (4.8) при b=Dх и m=1 ] sinj=l/ Dх. (9) Cледовательно Dрх=рl/ Dх. (10) Отсюда с учетом (1) получается соотношение DхDрх =рl=h (11) В общем случае соотношение DхDрх ³h, DyDрy ³h, DzDрz ³h (12) называют соотношением неопределенностей Гейзенберга. Из него следует, что чем точнее определена координата (Dх мало, т.е. узкая щель), тем больше неопределенность в импульсе частицы Dрх ³h/Dх. Точность определения импульса будет возрастать с увеличением ширины щели Dх [ cм. (9), (8)] и при Dх®¥ не будет наблюдаться дифракционная картина, и поэтому неопределенность импульса Dрх будет такой же, как и до прохождения частицы через щель, т.е. Dрх=0. Но в этом случае не определена координата х частицы, т.е. Dх®¥. Невозможность одновременно точно определить координату и импульс (скорость) не связана с несовершенством методов измерения или измерительных приборов. Соотношение неопределенности является квантовым ограничением применимости классической механики к микрообъектам. Выразим (11) в виде DхD v х ³h/m. (13) Из (13) следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости. Для пылинки массой 10-12 кг и линейными размерами 10-6 м, координата которой определена с точностью до 0.01 от ее размеров (т.е. Dх=10-8 м) неопределенность скорости согласно (13) D v х=6.62×10-31/(10-8×10-12)=6.62×10-14 м/c, т.е. будет ничтожно малой. Т. о. для макроскопических тел их волновые свойства не играют никакой роли, координата и скорость макротел могут быть измерены достаточно точно. В квантовой механике рассматривается также соотношение неопределенностей между энергией частицы Е и временем t нахождения частицы в данном энергетическом состоянии (или времени наблюдения за состоянием частицы). Оно аналогично (11) и имеет вид DЕDt³h (14) Из (14) следует, что частота излучения фотона также должна иметь неопределенность Dv ³DЕ/h (15) т.е. линии спектра должны характеризоваться частотой v±Dv. Действительно, опыт показывает, что все спектральные линии размыты. 9.3.Волновая функция и ее статистический смысл Мы привыкли к тому, что физически реальное - измеримо. Бор и Гейзенберг сделали обратное высказывание: " Принципиально неизмеримое - физически нереально." Поэтому "не надо говорить о вещах, которые невозможно измерить" (Фейнман). Поскольку из соотношения неопределенностей следует, что частица не имеет одновременно импульс и координату, то не следует об этом и говорить. А "говорить" следует о волновой функции, которая описывает микросостояние системы, ее волновые свойства. Де Бройль связал со свободно движущейся частицей плоскую волну. Известно [cм. (1.5), (1.6)], что плоская волна, распространяющаяся в направлении оси х описывается уравнением S=Acos(wt- kх+jО) или в экспоненциальной форме S=АOехр[i(wt- kх+jО)]. Заменив в соответствии с (1) и (2) w и k=2p/l через Е и p, уравнение волны де Бройля для свободной частицы пишут в виде Y=АOехр[(-i/ (в квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет çY÷ 2, то это [cм.(16)] несущественно). Функцию Y называют волновой функций или пси-функцией. Она, как правило, бывает комплексной. Интепретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того, что частица будет обнаружена в пределах объема dV: dP = çY÷ 2 dV=YY*dV (17) где Y* - комплексно - сопряженная волновая функция. Величина çY÷ 2=YY* = dP/ dV - имеет смысл плотности вероятности. Интеграл от (17), взятый по всему пространству, должен равняться единице (вероятность достоверного события Р=1).
Выражение (18) называют условием нормировки. Отметим еще раз, что волновая функция описывает микросостояние частицы, ее волновые свойства и она позволяет ответить на все вопросы, которые имеет смысл ставить. Например, найти энергию и импульс частицы. Для этого следует вычислить следующие частные производные Y по координате х и времени t:
откуда
9.4.Уравнение Шредингера для стационарных состояний В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение
где m - масса частицы, Решение уравнения Шредингера позволяет найти волновую функцию Y(x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства. Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя Y(x, y, z, t) = y(x, y, z) exp[-i(E/ где E/ В стационарном случае уравнение Шредингера имеет вид
где Е, U - полная и потенциальная энергия, m - масса частицы. Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений. 9.5. Собственные функции и собственные значения. Свободная частица Функции Y, удовлетворяющие уравнению Шредингера при данных U, называются собственными функциями. Значения Е, при которых существуют решения уравнения (22), называются собственными значениями. В качестве примера определим y и Е для свободной частицы. Свободной называют частицу, на которую не действуют силы, т.е.
Прямой подстановкой можно убедится, что частным решением этого уравнения является функция y(х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии Е= C учетом (21) волновая функция Y(х)=Аexp(-iwt+ ikx)= Аexp[-(i/ здесь w=Е/ Функция (25) представляет собой плоскую монохроматическую волну де Бройля [cм. (16)]. Из (24) следует, что зависимость энергии от импульса
Е= оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным. Плотность вероятности обнаружить частицу в данной точке пространства çy÷ 2=yy*=A2, т.е. все положения свободной частицы в пространстве являются равновероятными. 9.6. Частица в одномерной прямоугольной "потенциальной яме" Такая "яма" описывается потенциальной энергией вида
пределы "ямы", т.е. y(0)= y(l)=0. (27) В пределах ямы (0<x<l) уравнение (22) сведется к уравнению
где k2= y(х)=Аsinkx+Bcoskx (29) Так как согласно (27) ψ(0)=0, то В=0, тогда y(х)=Аsinkx. (30) Условие (27) y(l)=Аsinkl=0 выполняется только при kl=pn, где n=1,2... целые числа, т.е. необходимо, чтобы k=pn/l. (31) Из (29) и (31) следует, что
Таким образом, энергия в "потенциальной яме" принимает лишь определенные, дискретные значения, т.е. квантуется. Квантованные значения энергии Еn называются уровнями энергии, а число n, определяющее энергетические уровни, называется главным квантовым числом. Заметим, что n=1 cоответствует минимальная энергия Е1¹0. Подставив в (30) значения k из (31), найдем собственные функции
Постоянную А найдем из условия нормировки (18), которое для данного случая имеет вид
           Yn(x) n ½Yn(x)½2 n Yn(x) n ½Yn(x)½2 n  (33) (33)
              уровням энергии при n=1, 2, 3, приведены на рис. 5 (а). На рис. 5 (б) изображены плотности уровням энергии при n=1, 2, 3, приведены на рис. 5 (а). На рис. 5 (б) изображены плотности
          вероятности обнаружения частицы на различных вероятности обнаружения частицы на различных
   х расстояниях от "стенок" ямы х расстояниях от "стенок" ямы
9.7. Квантовый осциллятор Классическим осциллятором в классической механике называли частицу массой m, колеблющуюся с частотой w0=Ök/m под действием упругой силы F=-kx.
U=kx2/2=m Подставляя (34) в (22) и учитывая, что частица движется только вдоль одной прямой (вдоль оси х), получим
Решая уравнение (35), можно получить, что энергия (энергетический уровень) частицы принимает только дискретные значения (квантуется).
n=0,1,2... квантовые числа. Наименьшее значение энергии E0= Из (36) следует, что уровни находятся на равных расстояниях друг от друга
 x следовательно, может иметь любые значения. x следовательно, может иметь любые значения.
Рис. 7 В этом заключается принцип соответствия, сформулированный Бором в 1923 г.: При больших квантовых числах выводы и результаты квантовой механики должны соответсвовать выводам и результатам классической механики. Более общая трактовка принципа соответствия заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения. Причем в определенных, предельных случаях, новая теория переходит в старую.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.014 с.) |

 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) , т.е. изменяются в диапазоне длин волн обычных рентгеновских лучей (см. параграф 2.5).
, т.е. изменяются в диапазоне длин волн обычных рентгеновских лучей (см. параграф 2.5).
 источник е Узкий пучок электронов направлялся на поверхность
источник е Узкий пучок электронов направлялся на поверхность





 монокристалла никеля. Отраженные электроны
монокристалла никеля. Отраженные электроны


 улавливались цилиндрическим электродом (см. рис.1),
улавливались цилиндрическим электродом (см. рис.1),





 Ni присоединенным к гальванометру. Интенсивность
Ni присоединенным к гальванометру. Интенсивность




 Рис. 1 отраженного пучка оценивалась по силе тока, текущего
Рис. 1 отраженного пучка оценивалась по силе тока, текущего , опыт проводился при q =80°; с учетом этого и формулы (5) из (6) следует
, опыт проводился при q =80°; с учетом этого и формулы (5) из (6) следует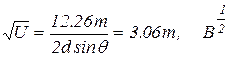 (7)
(7) Все это подтвердилось на опыте, особенно при больших значениях m (m=6, 7, 8). При определенных дискретных напряжениях, определяемых согласно (7), гальванометр фиксировал максимальный ток (рис.2). I
Все это подтвердилось на опыте, особенно при больших значениях m (m=6, 7, 8). При определенных дискретных напряжениях, определяемых согласно (7), гальванометр фиксировал максимальный ток (рис.2). I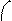



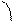


 Итак, опыт Девиссона-Джермера подтвердил Рис.2
Итак, опыт Девиссона-Джермера подтвердил Рис.2




 гипотезу де Бройля - движущиеся электроны ведут
гипотезу де Бройля - движущиеся электроны ведут
 опыты, подтверждающие волновые свойства микромира.
опыты, подтверждающие волновые свойства микромира.
 9.2. Соотношение неопределенностей Гейзенберга
9.2. Соотношение неопределенностей Гейзенберга Попытаемся определить значение координаты х
Попытаемся определить значение координаты х

 X Рис.3свободно летящей микрочастицы, поставив на ее пути
X Рис.3свободно летящей микрочастицы, поставив на ее пути

 щель шириной Dх, расположенную перпендикулярно
щель шириной Dх, расположенную перпендикулярно



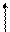 Dх р к направлению движения частицы.
Dх р к направлению движения частицы.

 точное значение, равное 0, так что неопределенность
точное значение, равное 0, так что неопределенность



 совершенно неопределенной. В момент прохождения
совершенно неопределенной. В момент прохождения (18)
(18)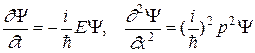
 (19)
(19) (20)
(20)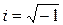 - мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа [ см. (1.10)].
- мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа [ см. (1.10)]. (22)
(22)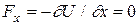 . Cледовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость
. Cледовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость  . Направим ось Х вдоль вектора
. Направим ось Х вдоль вектора  . Тогда (22) можно записать в виде
. Тогда (22) можно записать в виде . (23)
. (23) . (24)
. (24)


 0 l х При таком условии частица не проникает за
0 l х При таком условии частица не проникает за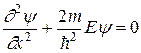 или
или  (28)
(28) . Общее решение (28)
. Общее решение (28) (32)
(32)

 В результате интегрирования получим
В результате интегрирования получим  , а собственные функции будут иметь вид
, а собственные функции будут иметь вид


 Из рис. следует, что, например, в квантовом состоянии с n=2 частица не может находится в середине "ямы", в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траектории частицы в квантовой механике несостоятельны.
Из рис. следует, что, например, в квантовом состоянии с n=2 частица не может находится в середине "ямы", в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траектории частицы в квантовой механике несостоятельны.





 Потенциальная энергия такой частицы U=kx2/2=m
Потенциальная энергия такой частицы U=kx2/2=m  x2/2; в точках с координатами ±хmax она равна полной энергии Е. Т.о., энергия частицы могла принимать любые значения, т.е. изменяться непрерывно (рис.6). E
x2/2; в точках с координатами ±хmax она равна полной энергии Е. Т.о., энергия частицы могла принимать любые значения, т.е. изменяться непрерывно (рис.6). E В квантовой механике понятие силы не используется, U Т
В квантовой механике понятие силы не используется, U Т поэтому квантовый осциллятор следует определить как
поэтому квантовый осциллятор следует определить как

 частицу с потенциальной энергией
частицу с потенциальной энергией (35)
(35)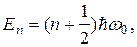 (36)
(36) (37)
(37)



 т.е. уровни эквидистантны [см. рис. 7, где на границе с потенциальной кривой U(x) U(±хmax)=Еn ]. При больших квантовых числах
т.е. уровни эквидистантны [см. рис. 7, где на границе с потенциальной кривой U(x) U(±хmax)=Еn ]. При больших квантовых числах n DЕ/Еn=1/(n+1/2)®0, т.е. происходит
n DЕ/Еn=1/(n+1/2)®0, т.е. происходит относительное сближение энергетических уровней
относительное сближение энергетических уровней
 и получаются результаты, близкие к результатам
и получаются результаты, близкие к результатам
 классического рассмотрения, когда энергия
классического рассмотрения, когда энергия частицы может изменяться непрерывно, и,
частицы может изменяться непрерывно, и,


