
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Шредингера для атома водорода. Квантовые числа и их физический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze(для атома водорода Z=1)
Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера, учитывающие значение U(r):
m-масса электрона, Е- полная энергия электрона в атоме. В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции ψnlm(r,θ,φ), определяемые 3 квантовыми числами: главным n,орбитальным l и магнитным ml. Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения n=1,2,3…. Орбитальное квантовое число l, при заданном n принимает значения l=0,1,…,(n-1) т.е. всего n значений и определяет момент импульса электрона в атоме. Магнитное квантовое число ml, при заданном l может принимать значения ml=0,±1,±2,…,±l, т.е. всего 2l+1 значений. Т.о. магнитное квантовое число определяет проекцию момента импульса на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
20.Собственный механический и магнитный момент электрона. Опыт Штерна и Герлаха. Электрон обладает собственным механическим моментом импульса Ls, называемым спином. Спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона соответствует собственный магнитный момент Ps, пропорциональный Ls и направленный в противоположную сторону: Ps=gsLs, gs – гиромагнитное отношение спиновых моментов. Проекция собственного магнитного момента на направление вектора B: PsB=±e`h/2m=±mB, где`h=h/2p, mB=магнетон Бора. Общий магнитный момент атома pa= векторной сумме магнитных моментов входящих в атом электрона: Pa=Spm+Spms. Опыт Штерна и Герлаха. Проводя измерения магнитных моментов они обнаружили, что узкий пучек атомов водорода в неоднородном магнитном поле расщепляется на 2 пучка. Хотя в этом состоянии (Атомы находились в S состоянии) момент импульса электрона равен 0, а так же магнитный момент атома равен 0, поэтому магнитное поле не оказывает влияние на движение атома водорода, то есть расщепления быть не должно. Однако, дальнейшие исследования показали что спектральные линии атомов водорода обнаруживают такую структуру даже в отсутствие магнитного поля. В последствии было установлено, что такая структура спектральных линий объясняется тем, что электрон обладает собственным неуничтожимым механическим моментом, названным спином.
21.Орбитальный, спиновый и полный угловой и магнитный момент электрона. Электрон обладает собственным моментом импульса MS, который называется спином. Его величина определяется по общим законам квантовой механики: MS=`hÖ[S(S+1)]=`hÖ[(1/2)*(3/2)]=(1/2)`hÖ3, Ml=`hÖ[l(l+1)] – орбитальный момент. Проекция может принимать квантовые значения, отличающиеся друг от друга на`h. MSz=mS`h, (ms=±S), Mlz=ml`h. Чтобы найти значение собственного магнитного момента умножим Ms на отношение ms к Ms, ms – собственный магнитный момент: ms=-eMs/mec=-(е`h/mec)Ö[S(S+1)]=-mБÖ3, mБ – Магнетон Бора. Знак (-) потому что Ms и ms направлены в разные стороны. Момент Электрона слагается из 2-х: орбитального Ml и спинового Ms. Это сложение осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов: Мj=`hÖ[j(j+1)], j – квантовое число полного момента импульса. 22. Атом во внешнем магнитном поле. Эффект Зеемана. Эффектом Зеемана называется расщепление энергетических уровней при действии на атомы магнитного поля. Расщепление уровней приводит к расщеплению спектральных линий на несколько компонентов. Расщепление спектральных линий при действии на излучающие атомы магнитного поля так же называется эффектом Зеемана. Зеемановское расщепление уровней обьясняется тем, что атом, обладающий магнитным моментом mj, приобретает в магнитном поле дополнительную энергию DE=-mjBB, mjB- проекция магнитного момента на направление поля. mjB=-mБgmj, DE=mБgmj, (mj=0, ±1,…, ±J). Энергетический уровень расщепляется на подуровни, причем величина расщепления зависит от квантовых чисел L,S,J данного уровня. 8) Основные постулаты квантовой механики. Вероятностный характер результатов измерений в квантовой механике. Первый постулат квантовой механики. Состояние частицы в квантовой механике описывается заданием волновой функции y(x,y,z,t), являющейся функцией пространственных координат и времени. Вероятностный смысл волновой функции. Квадрат модуля волновой функции y(x,y,z,t) определяет плотность вероятности w того, что в момент времени t³0 частица может быть обнаружена в точке пространства M=M(x,y,z) с координатами x, y и z. w=dP/dV=|y|2=y*y. Волновую функцию, удовлетворяющую условию нормировки F®¥ò|y|2dV=1, называют нормированной волновой функцией. Условия регулярности волновой функции. 1. Условие конечности волновой функции (волновая функция была квадратично интегрируемой функцией). 2. Условие однозначности волновой функции (плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно). 3. Условие непрерывности волновой функции. Кроме того, непрерывными должны быть также частные производные волновой функции, т.е. функция должна быть гладкой. Принцип суперпозиции. Если частица может находиться в квантовом состоянии, описываемом волновой функцией y1, а также в другом квантовом состоянии, описываемом волновой функцией y2, и т.д. аналогично до yn, то эта частица может также находиться в состоянии, описываемом волновой функцией y=с1y1+с2y2+…+сnyn. В таком состоянии квадрат модуля коэффициента Сn определяет вероятность того, что при измерении, проведенном над системой с такой волновой функцией, мы обнаружим ее в квантовом состоянии, описываемом волновой функцией yn. Поэтому для нормированных волновых функций
12) Частица в трехмерной потенциальной яме с абсолютно непроницаемыми стенками. Энергетический спектр частицы. Понятие о вырождении энергетических уровней. Потенциальный ящик: G={(x,y,z):0<x<a1,0<y<a2,0<z<a3}. U(x,y,z)={0: (x,y,z)ÎG, ¥: (x,y,z)ÏG}. Будем искать волновую функцию в виде произведения: y(x,y,z)= y1(x) y2(y) y3(z)=>(1/y1(x))(d2y1(x)/dx2)+ (1/y2(y))(d2y2(y)/dy2)+(1/y3(z)) (d2y3(z)/dz2)=-2m0E/ħ2. Первое слагаемое в левой части зависит только от x, а второе - только отy. Поскольку их сумма равна постоянной величине, то это означает, что каждое из слагаемых также представляет собой постоянную величину. Получаем три одномерных уравнения: d2y1(x)/dx2+2m0E1y1(x)/ ħ2=0, d2y2(y)/dy2+2m0E2y2(y)/ ħ2=0, d2y3(z)/dz2+2m0E3y3(z)/ ħ2=0=>
13) Движение микрочастицы в области одномерного потенциального порога. Надбарьерное отражение частицы в случае низкого порога. Потенциальный порог: U(x)={0: x<0; U0,x>0}. Пусть E<U0. Обозначив
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

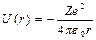 где r-расстояние между электроном и ядром
где r-расстояние между электроном и ядром
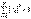 .
.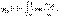 аналогично для y2(y) и y3(z)=>
аналогично для y2(y) и y3(z)=>  , а её энергетический спектр
, а её энергетический спектр  Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения или степенью вырождения уровня.
Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения или степенью вырождения уровня. и
и  получим ур-ние Шредингера в виде d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2-k22y2=0. Решением уравнения являются: y1(x)=A1exp{ik1x}+ B1exp{-ik1x} и y2(x)=A2exp{k2x}+ B2exp{-k2x}. Поскольку волновая функция должна быть ограниченной, а первое слагаемое в волновой функции y2(x) при x, стремящемся к бесконечности, неограниченно возрастает, то необходимо потребовать A2=0. Из условий сшивки y1(0)= y2(0) и y1’(0)= y2’(0)=> A1+B1=B2 и ik1A1-ik1B1=-k2B2. A1=1 => B1=(k1-ik2)/(k1+ik2); B2=2k1/(k1+ik2). =>y1(x)=exp{ik1x}+(k1-ik2)/(k1+ik2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{-k2x}. Коэф-т отражения R=|B1|2/|A1|2=1, коэф-т прохождения D=0. Пусть E>U0. Положим
получим ур-ние Шредингера в виде d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2-k22y2=0. Решением уравнения являются: y1(x)=A1exp{ik1x}+ B1exp{-ik1x} и y2(x)=A2exp{k2x}+ B2exp{-k2x}. Поскольку волновая функция должна быть ограниченной, а первое слагаемое в волновой функции y2(x) при x, стремящемся к бесконечности, неограниченно возрастает, то необходимо потребовать A2=0. Из условий сшивки y1(0)= y2(0) и y1’(0)= y2’(0)=> A1+B1=B2 и ik1A1-ik1B1=-k2B2. A1=1 => B1=(k1-ik2)/(k1+ik2); B2=2k1/(k1+ik2). =>y1(x)=exp{ik1x}+(k1-ik2)/(k1+ik2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{-k2x}. Коэф-т отражения R=|B1|2/|A1|2=1, коэф-т прохождения D=0. Пусть E>U0. Положим и
и  => d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2+k22y2=0=> y1(x)= A1exp{ik1x}+B1exp{-ik1x} и y2(x)=A2exp{ik2x}+ B2exp{-ik2x}. Поскольку отраженная волна в области II отсутствует, то B2 =0. Условие сшивки: A1+B1=A2 и k1A1-k1B1=k2B2. Полагая A1=1 => B1=(k1-k2)/(k1+k2); A2=2k1/(k1+k2) =>y1(x)=exp{ik1x}+(k1-k2)/(k1+k2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{ik2x}. R=|B1|2/|A1|2, D=|A2|2/|A1|2.
=> d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2+k22y2=0=> y1(x)= A1exp{ik1x}+B1exp{-ik1x} и y2(x)=A2exp{ik2x}+ B2exp{-ik2x}. Поскольку отраженная волна в области II отсутствует, то B2 =0. Условие сшивки: A1+B1=A2 и k1A1-k1B1=k2B2. Полагая A1=1 => B1=(k1-k2)/(k1+k2); A2=2k1/(k1+k2) =>y1(x)=exp{ik1x}+(k1-k2)/(k1+k2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{ik2x}. R=|B1|2/|A1|2, D=|A2|2/|A1|2.


