
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства волновой функции. Квантование.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Волновая функция (функция состояния, пси-функция) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному): Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния. Условия регулярности волновой функции: 1) Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл 2) Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным. 3) Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции
В физике квантование — построение квантового варианта некоторой неквантовой (классической) теории или физической модели в соответствии с аксиомами квантовой физики. Уравнение Шредингера вытекает в принцип квантования (дискретность). В соответствии с современной научной парадигмой фундаментальные физические теории должны быть квантовыми. Возможно, как построение изначально квантовых теорий, так и квантование классических моделей. Существует несколько математических методов квантования. Наиболее распространены: каноническое квантование, квантование методом функционального интеграла (фейнмановское квантование), BRST-квантование, геометрическое квантование, вторичное квантование. Эти методы не являются универсальными. Непосредственное применение тех или иных методов может оказаться невозможным. Например, в настоящий момент неизвестен метод построения квантовой теории гравитации. При квантовании модели могут возникать различные ограничения и физические эффекты. Например, различные квантовые теории струн могут быть сформулированы только для пространств определенной размерности (10, 11, 26 и т. д.). В теорие квантования также могут возникать новые объекты — квазичастицы.
Квантовые числа. Спин. Квантовое число — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы. Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) (nr), орбитальное (l) и магнитное (m) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно. Адроны— класс элементарных частиц, подверженных сильному взаимодействию. Спин — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы. Спин измеряется в единицах
Свойства ядерных сил. Ядерные силы - это силы притяжения, так как они удерживают нуклоны внутри ядра (при очень сильном сближении нуклонов ядерные силы между ними имеют характер отталкивания). Ядерные силы – это не электрические силы, так как они действуют не только между протонами, но и между не имеющими зарядов нейтронами, и не гравитационные, которые слишком малы для объяснения ядерных эффектов. Область действия ядерных сил, ничтожно мала. Радиус их действия 10-13. При больших расстояниях между частицами ядерное взаимодействие не проявляется. Ядерные силы (в той области, где они действуют) очень интенсивные. Их интенсивность значительно больше интенсивности электромагнитных сил, так как ядерные силы удерживают внутри ядра, одноимённо заряженные протоны, отталкивающиеся друг от друга с огромными электрическими силами. Изучение степени связанности нуклонов в разных ядрах показывают, что ядерные силы обладают свойством насыщения, аналогичным валентности химических сил. В соответствии с этим свойством ядерных сил один и тот же нуклон взаимодействует не со всеми остальными нуклонами ядра. А только с несколькими соседними. Важнейшим свойством ядерных сил является их зарядовая независимость, то есть тождественность трёх типов ядерного взаимодействия: между двумя протонами, между протоном и нейтроном и между двумя нейтронами.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.006 с.) |

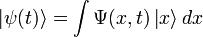 , где
, где 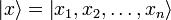 — координатный базисный вектор, а
— координатный базисный вектор, а 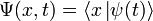 — волновая функция в координатном представлении.
— волновая функция в координатном представлении.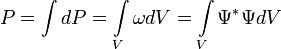 станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.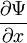 ,
, 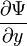 ,
, 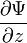 . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.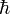 .
.


