
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корпускулярно—волновой дуализмСодержание книги
Поиск на нашем сайте
Гипотеза де Бройля. Дифракция электронов. Соотношение неопределенностей. Волновые свойства микрочастиц и соотношение неопределенностей. Волновая функция и ее статистический смысл. Амплитуда вероятностей.
Основные формулы
· Связь дебройлевской длины волны частицы с импульсом р
· Фазовая скорость свободно движущейся со скоростью
где · Групповая скорость свободно движущейся частицы
· Соотношение неопределенностей для координаты и импульса: где Для энергии и времени где · Вероятность нахождения частицы в объеме
где
Семестровые задания
28.1. Протон обладает кинетической энергией Т = 1кэВ. Определить дополни-тельную энергию 28.2. Определить длины волн де Бройля 28.3. Электрон обладает кинетической энергией Т =1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия Т электрона уменьшится вдвое? 28.4. Кинетическая энергия Т электрона равна удвоенному значению его энергии покоя. Вычислить длину волны l де Бройля для такого электрона. 28.5. Найти длину волны де Бройля для электронов, прошедших разность потенциалов 100 В. 28.6. Используя соотношение неопределенностей, оценить ширину 28.7.Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину 28.8. Используя соотношение неопределенностей, оценить наименьшие ошибки в определении импульса электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 28.9. Определить относительную неопределенность 28.10. Принимая, что электрон находится внутри атома диаметром d=0,3 нм, определить неопределенность энергии данного электрона.
Уравнение Шредингера.
Временноеуравнение Шредингера. Стационарное уравнение Шредингера. Частица в одномерной прямоугольной потенциальнойяме. Прохождение частицычерез потенциальный барьер.
Основные формулы
· Коэффициент прозрачности конечной ширины
где · Одномерное уравнение Шредингера для стационарных состояний
где · Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика: а) б)
Семестровые задания.
29.1. Написать уравнение Шредингера для линейного гармонического осциллятора. Учесть, что сила, возвращающая частицу в положение равновесия, ¦ = - кх (где к – коэффициент пропорциональности, х - смещение). 29.2. Временная часть уравнения Шредингера имеет вид 29.3.Написать уравнение Шредингера для свободного электрона, движущегося в положительном направлении оси Х со скоростью 29.4. Электрон находится в бесконечно глубоком прямоугольном одномерном потенциальном ящике шириной 29.5.Электрону в потенциальном ящике шириной 29.6. Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней 29.7. Электрон находится в потенциальном ящике шириной 29.8. Электрон находится в одномерном потенциальном ящике шириной 29.9. Электрон находится в одномерной прямоугольной потенциальной яме шириной 29.10. В прямоугольной потенциальной яме шириной
Конденсированное состояние
Элементы структурной кристаллографии. Методы исследования кристаллических структур. Теплоемкость кристаллической решетки. Фононный газ. Размерный эффект в теплопроводности кристаллов. Носители тока как квазичастицы. Энергетические зоны в кристаллах. Уровень Ферми. Поверхность Ферми. Металлы, диэлектрики и полупроводники в зонной теории. Понятие дырочной проводимости. Собственная и примесная проводимость. Явление сверхпроводимости. Куперовское спаривание. Кулоновское отталкивание и фононное притяжение. Эффект Джозефсона. Квантовые представления о свойствах ферромагнетиков. Обменное взаимодействие. Температура Кюри. Намагничивание ферромагнетиков.
Основные формулы
· Средняя энергия квантового одномерного осциллятора
где · Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов,
где · Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая)
· Теплота, необходимая для нагревания тела,
где · Удельная проводимость собственных полупроводников
где · Сила тока в
где · Внутренняя контактная разность потенциалов
где
Семестровые задания
30.1. Вычислить удельную теплоемкость с кристалла меди по классической теории теплоемкости. 30.2. Пользуясь классической теорией вычислить удельную теплоемкость кристалла NaCl. 30.3. Вычислить по классической теории теплоемкости теплоемкость С кристалла бромида алюминия 30.4. Масса кристалла никеля равна 20 г. Вычислить теплоемкость С при нагревании его от 0оС до 200оС. 30.5. Вычислить значение средней энергии 30.6. Найти частоту 30.7. Во сколько раз изменится средняя энергия 30.8. Определить отношение 30.9. Используя квантовую теорию теплоемкости Эйнштейна, определить изменение 30.10. Пользуясь теорией теплоемкости Эйнштейна, определить изменение
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.01 с.) |

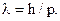
 частицы массой
частицы массой 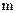
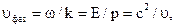
 энергия частицы (
энергия частицы (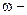 круговая частота);
круговая частота);  импульс
импульс 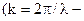 волновое число).
волновое число).
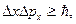
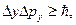

 неопределенности координат;
неопределенности координат;  неопределенности соответствующих проекций импульса частицы на оси координат.
неопределенности соответствующих проекций импульса частицы на оси координат.
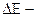 неопределенность энергии данного квантового состояния;
неопределенность энергии данного квантового состояния;  время пребывания системы в данном состоянии.
время пребывания системы в данном состоянии.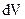
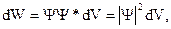
 волновая функция, описывающая состояние частицы;
волновая функция, описывающая состояние частицы;  функция, комплексно сопряженная с
функция, комплексно сопряженная с  ;
;  квадрат модуля волновой функции является плотностью вероятности нахождения частицы вблизи точки с координатой х.
квадрат модуля волновой функции является плотностью вероятности нахождения частицы вблизи точки с координатой х. , которую необходимо ему сообщить для того, чтобы длина волны
, которую необходимо ему сообщить для того, чтобы длина волны  де Бройля уменьшилась в три раза.
де Бройля уменьшилась в три раза. частицы и протона, прошедших одинаковую ускоряющую разность потенциалов U = 1 кВ.
частицы и протона, прошедших одинаковую ускоряющую разность потенциалов U = 1 кВ. одномерного потенциального ящика, в котором минимальная энергия электрона
одномерного потенциального ящика, в котором минимальная энергия электрона  = =10 эВ.
= =10 эВ. -частицы
-частицы 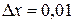 мм.
мм.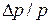 импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля.
импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля. прямоугольного потенциального барьера
прямоугольного потенциального барьера
 множитель, который можно приравнять к единице;
множитель, который можно приравнять к единице;  высота потенциального барьера;
высота потенциального барьера;  энергия частицы.
энергия частицы. ,
, - волновая функция, описывающая состояние частицы;
- волновая функция, описывающая состояние частицы;  - масса частицы; Е- полная энергия;
- масса частицы; Е- полная энергия;  - потенциальная энергия частицы.
- потенциальная энергия частицы.
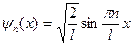 (собственная нормированная волновая функция);
(собственная нормированная волновая функция); (собственное значение энергии), где
(собственное значение энергии), где  – ширина потенциального ящика,
– ширина потенциального ящика,  = 1,2,3…
= 1,2,3… . Найти решение уравнения.
. Найти решение уравнения. (n = 1,2,3,…). Используя связь энергии Е электрона с волновым числом к, получить выражения для собственных значений Еn.
(n = 1,2,3,…). Используя связь энергии Е электрона с волновым числом к, получить выражения для собственных значений Еn.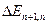 к энергии частицы Еn при n ® ¥.
к энергии частицы Еn при n ® ¥. с абсолютно непроницаемыми стенками (0 < х <
с абсолютно непроницаемыми стенками (0 < х < 

 нулевая энергия
нулевая энергия  ;
; 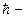 постоянная Планка;
постоянная Планка;  круговая частота колебаний осциллятора;
круговая частота колебаний осциллятора;  постоянная Больцмана;
постоянная Больцмана;  термодинамическая температура.
термодинамическая температура.
 молярная газовая постоянная;
молярная газовая постоянная;  характеристическая темпера-тура Эйнштейна;
характеристическая темпера-тура Эйнштейна;  молярная нулевая энергия (по Эйнштейну).
молярная нулевая энергия (по Эйнштейну).

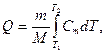
 масса тела;
масса тела;  молярная масса;
молярная масса;  и
и 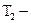 начальная и конечная температуры тела.
начальная и конечная температуры тела. ,
, ширина запрещенной зоны;
ширина запрещенной зоны;  константа.
константа. переходе
переходе ,
, предельное значение силы обратного тока;
предельное значение силы обратного тока;  внешнее напряжение, приложенное к
внешнее напряжение, приложенное к 
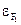 и
и  энергия Ферми соответственно для первого и второго металлов;
энергия Ферми соответственно для первого и второго металлов; 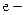 заряд электрона.
заряд электрона.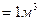 . Плотность
. Плотность  кристалла бромида алюминия равна 3,01×103 кг/м3.
кристалла бромида алюминия равна 3,01×103 кг/м3.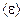 классического линейного гармонического осциллятора при Т = 300 К.
классического линейного гармонического осциллятора при Т = 300 К. колебаний атомов серебра по теории теплоемкости Эйнштейна, если характеристическая температура QE серебра равна 165 К.
колебаний атомов серебра по теории теплоемкости Эйнштейна, если характеристическая температура QE серебра равна 165 К. E /2 до Т2 =
E /2 до Т2 =  средней энергии квантового осциллятора к средней энергии теплового движения молекул идеального газа при температуре Т =
средней энергии квантового осциллятора к средней энергии теплового движения молекул идеального газа при температуре Т =  молярной внутренней энергии кристалла при нагревании его на
молярной внутренней энергии кристалла при нагревании его на  от температуры Т =
от температуры Т =  .Характеристическая температура данного кристалла равна 300 К.
.Характеристическая температура данного кристалла равна 300 К.


