
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика материальной точки и твердого телаСодержание книги
Поиск на нашем сайте
Законы Ньютона. Масса. Сила. Виды сил в механике. Гравитационные силы. Закон всемирного тяготения. Силы упругости. Закон Гука. Силы трения. Инерциальные системы отсчета. Механический принцип относительности. Преобразования Галилея. Неинерциальные системы отсчета. Силы инерции. Понятие абсолютно твердого тела. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Момент силы и момент инерции твердого тела. Теорема Штейнера.
Основные формулы
· Импульс (количество движения) материальной точки
·Второй закон Ньютона (основное уравнение динамики материальной точки). · Сила трения скольжения где · Сила упругости
где · Потенциальная энергия упругодеформированного тела
где · Напряжение при упругой деформации
где · Закон Гука для продольного растяжения (сжатия)
где · Закон всемирного тяготения
где · Сила тяжести
где · Напряженность поля тяготения
где · Потенциальная энергия гравитационного взаимодействия двух материальных точек массами
· Потенциал поля тяготения
где П- потенциальная энергия материальной точки массой · Связь между потенциалом поля тяготения и его напряженностью
где · Момент инерции материальной точки относительно некоторой оси вращения
где m – масса точки; r- расстояние от нее до оси вращения. · Момент инерции системы (тела) относительно некоторой оси вращения
где · Теорема Штейнера
где · Кинетическая энергия тела, вращающегося вокруг неподвижной оси
где · Момент силы относительно неподвижной точки
где
где · Работа при вращении тела
где
Семестровые задания
2.1. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m1 = 100г и m2 = 120г. Найти ускорение, с которым движутся грузики, если масса 2.2. На барабан массой m = 9 кг намотан шнур, к концам которого привязан груз массой m1 = 2 кг. Определить ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь. 2.3. На барабан радиусом R = 0,5 м намотан шнур, к концам которого привязан груз массой m = 9,8 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением а =2,04 м/с2. 2.4. Тонкий однородный стержень длиной 2.5.Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1 = 0,3 кг и m2 = 0,5 кг. Определить силы Т1 и Т2 натяжения шнурa по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. 2.6. Шар массойm = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шараимеет вид j=A+Bt2+Ct3, где В = 4 рад/с2, С = I рад/с3. Найти закон изменения момента сил, действующих на шар. Определить момент сил в момент времени t = 2 с. 2.7. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению j = At+Bt3, где А = 2рад/с, В = 0,2 рад/с3. Определить вращающиймомент М, действующий на стержень через время t = 2с после начала враще-ния, еслимомент инерции стержня 2.8. Вал маccойm = 100 кг и радиусомR = 5 cм вращался с частотойn = 8 с-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40Н, под действием которой вал остановился через t =10 с. Определить коэффициент трения f. 2.9. На обод маховика диаметром D = 60 cм намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжеcти груза, за время t = 3c приобрел угловую скорость w = 9 рад/с. 2.10. Определить момент силыМ, который необходимо приложить к блоку, вращающемуся с частотой n = 12с-1, чтобы он остановился в течение времени t=8c. Диаметр блока D = 30 cм. Массу блока m = 6кг считать равномерно распределенной по ободу. 2.11. Шарик массой m = 60 г, привязанный к концу нити длиной 2.12. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой т = 40 кг приложена сила F = 1 кН. Определить угловое ускорение e и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь. 2.13. К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 100 Н. При вращении диска на него действует момент сил трения М = 2 Н∙м. Определить массу диска, если его угловое ускорение 2.14. Через неподвижный блок в виде однородного сплошного цилиндра массой m = 1 кг перекинута невесомая нить, к концам которой прикреплены тела массами m1 = 1 кг и m2 = 2 кг. Найти ускорение грузов. Трением в оси блока пренебречь. 2.15. На вал массой m1 = 20 кг намотана нить, к концу которой привязали груз массой m2 = 1 кг. Определить ускорение груза, опускающегося под действием силы тяжести. Трением пренебречь. 2.16. Определить линейную скорость центра шара, скатившегося без скольжения с наклонной плоскости высотой 1 м. 2.17. Определить скорость поступательного движения сплошного цилиндра, скатившегося без скольжения с наклонной плоскости высотой h = 20 см. 2.18. Вычислить момент инерции тонкого обода радиусом r = 30 см и массой 5 кг относительно оси, проходящей через конец диаметра перпендикулярно к плоскости обода. 2.19. Диск радиусом 30 см и массой 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости, с частотой n = 20 об/с. Какую работу надо совершить, чтобы остановить диск? 2.20.Маховик в виде диска массой m = 80 кг и радиусом 0,3 м находится в покое. Какую работу нужно совершить, чтобы сообщить маховику частоту n = =10с-1?
Законы сохранения
Законы сохранения как следствие симметрии пространства и времени. Система материальных точек. Внешние и внутренние силы. Центр масс (центр инерции) механической системы и закон его движения. Закон сохранения импульса как фундаментальный закон природы. Реактивное движение. Уравнение Мещерского. Движение в центральном поле. Законы Кеплера. Энергия как универсальная мера различных форм движения и взаимодействия. Работа силы и ее выражение через криволинейный интеграл. Мощность. Кинетическая энергия механической системы и ее связь с работой внешних и внутренних сил, приложенных к системе. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку. Консервативные и неконсервативные силы. Закон сохранения энергии в механике. Момент импульса. Закон сохранения момента импульса. Гироскопический эффект.
Основные формулы
Закон сохранения импульса для замкнутой системы
где · Работа, совершаемая постоянной силой,
где · Работа, совершаемая переменной силой, на пути
· Кинетическая энергия движущегося тела
· Связь между силой, действующей на тело в данной точке поля, и потенциальной энергией частицы
где · Потенциальная энергия тела, поднятого над поверхностью Земли на высоту
где · Закон сохранения механической энергии Т + П = Е = соnst. · Момент импульса (момент количества движения) твердого тела относительно оси вращения
где · Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси.
где · Закон сохранения момента импульса (момента количества движения) для замкнутой системы
Семестровые задания
3.1. Шар массой m1 = 4 кг движется со скоростью 3.2. Ядро, летевшее в горизонтальном направлении со скоростью 3.3. Два человека на роликовых коньках стоят друг против друга. Масса первого человека 60 кг, а второго 70 кг. Первый бросает второму груз массой m = =5 кг со скоростью, горизонтальная составляющая которой 3.4. На краю неподвижной скамьи Жуковского диаметром 60 см и массой m1=8 кг стоит человек массой m2 = 70 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 50 см от оси скамьи. Скорость мяча 3.5. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости 3.6. Маховик вращается по закону, выражаемому уравнением 50 кгм2. Найти законы, по которым меняются вращающий момент М и мощность N. 3.7. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия Т шара равна 14 Дж. Определить кинетическую энергию Т1 поступательного и Т2 вращательного движений. 3.8. Шар диаметром 6см катится без скольжения по горизонтальной плоскости, делая 4 оборота в секунду. Масса шара m = 0,25 кг. Найти кинетическую энергию шара. 3.9. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска. 3.10. Маховик в виде диска массой m = 80 кг и радиусом R = 30 см находится в состоянии покоя. Какую работу А нужно совершить, чтобы сообщить маховику частоту n = 10 с-1? 3.11. Горизонтальная платформа в форме диска массой m1= 100 кг и радиусом R = 2 м вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n1 = 10 об/мин-1. С какой частотой n2 начнет вращаться платформа, если человек массой m2 = 60 кг перейдет от края платформы к ее центру. 3.12. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n1 = 10 мин-1, стоит человек массой m = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2 = 12мин-1. Определить массу m2 платформы. Момент инерции человека рассчитывать как для материальной точки. 3.13. С поверхности Земли вертикально вверх пущена ракета со скоростью
3.14. Период Т вращения искусственного спутника Земли равен 2 ч. Считая орбиту спутника круговой, найти на какой высоте h над поверхностью Земли движется спутник. 3.15. Радиус R малой планеты равен 250 км, средняя плотность r = 3 г/см3. Ускорение свободного падения g на поверхности планеты неизвестно. Определить его. 3.16. Радиус R планеты Марс равен 3,4 Мм, его масса т = 6,4×1023 кг. Определить напряженность G гравитационного поля на поверхности Марса. 3.17. Найти первую и вторую космические скорости вблизи поверхности Солнца. 3.18. На какую высоту h над поверхностью Земли поднимается ракета, пущенная вертикально вверх, если начальная скорость 3.19. Какова будет скорость 3.20. Ракета, пущенная вертикально вверх, поднялась на высоту h = 3200 км и начала падать. Какой путь S пройдет ракета за первую секунду своего падения?
§ 4. Элементы специальной теории относительности
Постулаты Эйнштейна. Преобразования Лоренца. Инварианты преобразований. Релятивистский закон сложения скоростей. Преобразование импульса и энергии.
Основные формулы
· Преобразование Лоренца
где предполагается, что система отсчета · Релятивистское замедление хода часов
где · Релятивистское (лоренцево) сокращение длины
где · Релятивистский закон сложения скоростей
где предполагается, что система отсчета · Интервал
где · Масса и импульс частицы
где · Основной закон релятивистской динамики
где · Полная и кинетическая энергии частицы
· Связь между энергией и импульсом частицы
Семестровые задания
4.1. Кинетическая энергия электрона равна 2 МэВ. Определить скорость электрона. 4.2. Протон с кинетической энергией Т = 3 ГэВ при торможении потерял треть этой энергии. Определить импульс частицы. 4.3. При какой скорости 4.4. Определить импульс электрона, кинетическая энергия которого 1 ГэВ. 4.5. До какой скорости нужно разогнать электрон, чтобы его масса была в 2 раза больше массы покоя? 4.6. Электрон движется со скоростью, равной 4.7. Какова масса протона в системе отсчета, относительно которой он движется со скоростью 4.8. Какую скорость 4.9. Скорость электрона 4.10. Протон обладал кинетической энергией, равной энергии покоя. Определить импульс частицы (в единицах mо×с).
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.182 (0.013 с.) |

 .
.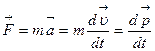 .
. ,
, - коэффициент трения скольжения;
- коэффициент трения скольжения;  - сила нормального давления.
- сила нормального давления. ,
,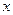 – деформация;
– деформация;  - коэффициент упругости.
- коэффициент упругости. ,
, - масса точки;
- масса точки;  - расстояние от нее до оси вращения.
- расстояние от нее до оси вращения. ,
, - растягивающая (сжимающая) сила;
- растягивающая (сжимающая) сила;  - площадь поперечного сечения.
- площадь поперечного сечения. ,
, - модуль Юнга,
- модуль Юнга,  - относительное удлинение (сжатие).
- относительное удлинение (сжатие). ,
,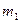 и
и  ;
; 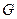 - гравитационная постоянная.
- гравитационная постоянная. ,
, - ускорение свободного падения.
- ускорение свободного падения. ,
, .
. ,
, или
или  ,
, - единичные векторы координатных осей.
- единичные векторы координатных осей. ,
,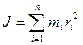 ,
, расстояние материальной точки массой
расстояние материальной точки массой 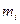 до оси вращения. В случае равномерного распределения масс
до оси вращения. В случае равномерного распределения масс  .
. ,
, - момент инерции тела относительно произвольной оси;
- момент инерции тела относительно произвольной оси;  - момент инерции относительно оси, параллельной данной и, проходящей через центр масс тела;
- момент инерции относительно оси, параллельной данной и, проходящей через центр масс тела;  -расстояние между осями.
-расстояние между осями.
 ,
, - момент инерции тела относительно оси
- момент инерции тела относительно оси 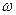 - угловая скорость тела.
- угловая скорость тела. ,
, -радиус- вектор, проведенный из этой точки в точку приложения силы
-радиус- вектор, проведенный из этой точки в точку приложения силы  . Модуль момента силы
. Модуль момента силы ,
, - плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
- плечо силы (кратчайшее расстояние между линией действия силы и осью вращения). ,
, - угол поворота тела;
- угол поворота тела;  - момент силы относительно оси
- момент силы относительно оси  = 50 см и массой m = 400 г вращается с угловым ускорением e = 3 рад/с2 около оси, проходящей перпен-дикулярно стержню через его середину. Определить вращающий момент М.
= 50 см и массой m = 400 г вращается с угловым ускорением e = 3 рад/с2 около оси, проходящей перпен-дикулярно стержню через его середину. Определить вращающий момент М. = l,2 м, вращается с частотой n1 = 2с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния
= l,2 м, вращается с частотой n1 = 2с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния  = 0,6 м. С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
= 0,6 м. С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. = 12 рад/с2.
= 12 рад/с2.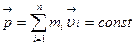 ,
, - число материальных точек (или тел), входящих в систему.
- число материальных точек (или тел), входящих в систему. ,
, - проекция силы на направление перемещения; a- угол между направлениями силы и перемещения.
- проекция силы на направление перемещения; a- угол между направлениями силы и перемещения.
 .
. .
. или
или  ,
, - единичные векторы координатных осей.
- единичные векторы координатных осей. .
.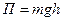 ,
, ,
, - расстояние от оси
- расстояние от оси  - импульс этой частицы;
- импульс этой частицы;  ;
;  ,
, .
.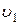 = 5 м/с и сталкивается с шаром массой m2 = 6 кг, который движется ему навстречу со скоростью
= 5 м/с и сталкивается с шаром массой m2 = 6 кг, который движется ему навстречу со скоростью  =2 м/с. Считая удар прямым, центральным, а шары абсолютно упругими, найти их скорость после удара.
=2 м/с. Считая удар прямым, центральным, а шары абсолютно упругими, найти их скорость после удара.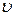 = 10 м/с, разорвалась на две части. Массы осколков равны 8 кг и 4 кг. Скорость меньшего осколка равна
= 10 м/с, разорвалась на две части. Массы осколков равны 8 кг и 4 кг. Скорость меньшего осколка равна  = 1 м и высотой h = 20 см?
= 1 м и высотой h = 20 см? , где А = 2 рад; В = 16 рад/с; С = -2 рад/с2. Момент инерции J колеса равен
, где А = 2 рад; В = 16 рад/с; С = -2 рад/с2. Момент инерции J колеса равен = 5 км/с. На какую высоту она поднимется?
= 5 км/с. На какую высоту она поднимется? = 10 км/с? Сопротивление воздуха не учитывать. Радиус R Земли и ускорение свободного падения
= 10 км/с? Сопротивление воздуха не учитывать. Радиус R Земли и ускорение свободного падения  ;
;  ;
; 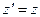 ;
;  ,
, движется со скоростью
движется со скоростью  , причем оси
, причем оси  и
и  и
и  и
и  и
и 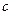 - скорость распространения света в вакууме.
- скорость распространения света в вакууме. ,
, - промежуток времени между двумя событиями, отсчитанный движущимися вместе с телом часами;
- промежуток времени между двумя событиями, отсчитанный движущимися вместе с телом часами;  - промежуток времени между теми же событиями, отсчитанный покоящимися часами.
- промежуток времени между теми же событиями, отсчитанный покоящимися часами. ,
, - длина стержня, измеренная в системе отсчета, относительно которой стержень покоится (собственная длина);
- длина стержня, измеренная в системе отсчета, относительно которой стержень покоится (собственная длина); 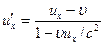 ;
;  ;
;  ,
, ,
,  между событиями (инвариантная величина)
между событиями (инвариантная величина) ,
, - промежуток времени между событиями 1 и 2;
- промежуток времени между событиями 1 и 2;  - расстояние между точками, где произошли события.
- расстояние между точками, где произошли события.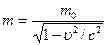 ;
;  ,
, - масса покоя.
- масса покоя. ,
, - импульс частицы.
- импульс частицы. ,
,  .
. ,
,  .
.


