
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о геометрической оптикеСодержание книги
Поиск на нашем сайте
Законы отражения и преломления. Явление внутреннего отражения. Оптические приборы. Фотометрия. Основные формулы
· Законы отражения и преломления света
где · Предельный угол полного внутреннего отражения при распространении света из оптически более плотной среды в оптически менее плотную
· Формула сферического зеркала
где а и · Оптическая сила тонкой линзы
где · Сила света
где d · Полный световой поток, испускаемый изотропным точечным источником
где · Светимость поверхности
где · Яркость
где · Освещенность Е поверхности
где · Связь светимости направления,
Семестровые задания
22.1. В воздухе на стеклянную пластину с показателем преломления n=1,5 падает луч света. Определить угол падения зная, что отраженный луч перпендикулярен преломленному лучу. 22.2. На плоскопараллельную стеклянную пластинку толщиной d = 5 см падает под углом 300 луч света. Показатель преломление n =1,5. Определить смещение луча, прошедшего сквозь эту пластинку. 22.3. Расстояние от предмета до вогнутого сферического зеркала a=2R. Определить положение изображения, если радиус кривизны равен 30 см. 22.4. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в два раза. Расстояние а от предмета до зеркала равно 30 см. Определить радиус кривизны зеркала. 22.5. Фокусное расстояние вогнутого зеркала равно 20 см. Зеркало дает действительное изображение предмета, уменьшенное в три раза. Определить расстояние а от предмета до зеркала. 22.6. Луч света падает на трехгранную призму из кварцевого стекла под углом 360. Преломляющий угол призмы равен 400. Каков его угол отклонения от первоначального направления? 22.7. Определить угол отклонения 22.8. Определить угол отклонения луча стеклянной призмой, преломляющий угол 22.9. Радиусы кривизны поверхностей двояковыпуклой стеклянной линзы, находящейся в воде, равны 50 см каждый. Определить оптическую силу линзы. 22.10. Необходимо изготовить плосковыпуклую линзу с оптической силой 5дптр. Определить радиус кривизны выпуклой поверхности линзы, если показатель преломления материала линзы n = 1,5. 22.11. Найти предельный угол полного внутреннего отражения для поверхности раздела: 1) стекло-воздух; 2) вода-воздух. Показатели преломления стекла n = 1,5; воды n = 1,33. 22.12. Предельный угол падения при переходе луча из скипидара в воздух равен 410 22.13. Главное фокусное расстояние собирающей линзы в воздухе равно 10см. Определить, чему оно равно в воде. 22.14. Двояковыпуклая линза с показателем преломления n =1,5 имеет одина-ковые радиусы кривизны поверхностей R1=R2=15 см. Изображение предмета с помощью этой линзы оказывается в 5 раз больше предмета. Определить расстояние от предмета до изображения. 22.15. Найти оптическую силу и фокусное расстояние тонкой стеклянной линзы в жидкости с показателем преломления n0 = 1,7, если ее оптическая сила в воз-духе Д0 =-5 дптр. 22.16. Светильник в виде равномерно светящегося шара радиусом R = 15 см имеет силу света I = 100 кд. Определить полный световой поток Ф и светимость R. 22.17. Определить световой поток, падающий на площадку S = 15 см2, распо-ложенную на расстоянии 2 м от источника, сила света которого I = 100 кд. 22.18. Найти освещенность края стола диаметром 1 м, если он освещается лампой, висящей на высоте 1 м от центра стола. Полный световой поток лампы Ф = =600 лк. 22.19. На высоте h =3 м над землей и на расстоянии l = 4 м от стены висит лам-па силой света I = 200 кд. Определить освещенность Е1 стены и Е2 горизонталь-ной поверхности земли у линии их пересечения. 22.20. На какой высоте h над центром круглого стола диаметром d =2 м нужно повесить лампочку, чтобы освещенность на краю стола была максимальной?
Свойства световых волн
Волновой пакет. Групповая скорость света. Интерференция световых волн. Когерентность. Интерференция квазимонохроматических волн. Интерферометры.
Основные формулы
· Скорость света в среде
где с – скорость света в вакууме, n – абсолютный показатель преломления среды. · Оптический путь световой волны L = n × l, где l – геометрическая длина пути световой волны в среде с показателем преломления n. · Оптическая разность хода двух световых волн D=L1 – L2 · Ширина интерференционной полосы от двух когерентных источников света (зеркала и бипризма Френеля, метод Юнга).
где l - длина световой волны, · Условие максимумов интенсивности света при интерференции D = ± kl (k = 0,1,2,3....). · Условие минимумов интенсивности света при интерференции D = ± (2k+1) l / 2. Условия максимума и минимума интенсивности света при наблюдении интерференции света в тонких плоскопараллельных пластинках в отраженном свете
D = 2d или D = 2dn cos i2 -l/2 = ± (2 k + 1) l / 2 (min),
где d - толщина пластинки (или пленки), i1 - угол падения, i2- угол преломления, n - показатель преломления материала пластинки, k = 0,1,2,3.... При интерференции света в проходящем свете условия максимума и минимума меняются местами. · Связь разности фаз Dj колебаний с оптической разностью хода световых волн Dj = 2pD / l · Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем
где k - номер кольца (k= 1,2,3...); R- радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластиной. · Радиусы темных колец в отраженном свете (или светлых в проходящем).
Семестровые задания
23.1. На мыльную пленку падает белый свет под углом 450 к поверхности пленки. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый свет (l = 600нм)? Показатель преломления мыльной воды n = 1,33. 23.2. На мыльную пленку с показателем преломления n = 1,33 падает по норма-ли монохроматический свет с длиной волны 0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая, возможная толщина пленки? 23.3. На стеклянную пластинку нанесен тонкий слой прозрачного вещества с показателем преломления n = 1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны l = 640нм, падающим на пластинку нормально. Какую минимальную толщину должен иметь слой, чтобы отраженный пучок имел наименьшую яркость? 23.4. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 8,6 м. Радиус четвертого темного кольца в отраженном свете r4 = 4,5мм. Найти длину волны l падающего света. 23.5. Установка для получения колец Ньютона освещается белым светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 5м. Наблюдение ведется в проходящем свете. Найти радиус четвертого кольца (l = 400нм). 23.6. Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны (l = 500 нм), падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластинкой заполнено водой. Найти толщину h слоя воды между линзой и пластинкой в том месте, где наблюдается третье светлое кольцо в отраженном свете. 23.7. Радиус второго кольца Ньютона в отраженном свете r2 = 0,4 мм. Опре-делить радиус R кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны l = 0,64 мкм. 23.8. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. После того как пространство между линзой и стеклянной пластинкой заполнили жидкостью, радиусы темных колец в отраженном свете уменьшились в 1,25 раза. Найти показатель преломления n жидкости. 23.9. Плосковыпуклая линза с фокусным расстоянием f = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете 1,1 мм. Определить длину световой волны. 23.10. На поверхность стеклянного объектива (n1 = 1,5) нанесена тонкая пленка, показатель преломления которой n2 = 1,2 («просветляющая» пленка). При какой наименьшей толщине этой пленки произойдет максимальное ослабление отраженного света в средней части видимого спектра l = 550 нм? 23.11.Пучок белого света падает по нормали к поверхности стеклянной пластинки толщиной 0,4 мкм. Показатель преломления стекла n = 1,5. Какие длины волн, лежащие в пределах видимого спектра (от 400 до 700 нм), усиливаются в отраженном свете? 23.12. В опыте Юнга щели, расположенные на расстоянии d = 0,3 мм освеща-лись многохроматическим светом с длиной волны 0,6 мкм. Определить расстояние от щелей до экрана, если ширина интерференционных полос равна 1мм. 23.13. Расстояние l от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l = 10 мм укладывается N = =10 темных интерференционных полос. Длина волны 23.14. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света d = 0,5 мм, расстояние до экрана l = 5 м. В зеленом свете интерференционные полосы получились на расстоянии 5 мм друг к другу. Найти длину волны зеленого света. 23.15. Для наблюдения интерференции от зеркал Френеля два плоских зеркала расположили под углом =10 см от узкой щели, параллельной обоим зеркалам. Определить длину волны света, если ширина интерференционных полос 23.16. В интерферометре Жамена на пути интерферирующих лучей помещены две одинаковые трубки, закрытые прозрачными пластинками. Одна заполнена воздухом при нормальных условиях, а из другой он выкачан. При выкачивании воздуха интерференционная картина сместилась на m = 20 полос. Длина трубок l = 5 см. Определить показатель преломления воздуха. 23.17. В интерферометр Жамена помещены две трубки длиной 23.18. В опыте с интерферометром Майкельсона для смещения интерферен-ционной картины на m = 450 полос зеркало пришлось переместить на рас-стояние 0,135 мм. Определить длину волны падающего света. 23.19. В опыте с интерферометром Майкельсона первоначальная интерферен-ционная картина сместилась на m = 450 полос. Определить перемещение x зеркала в интерферометре, если длина световой волны 23.20. В одно из плеч интерферометра Майкельсона поместили откачанную трубку длиной
§ 24. Дифракция волн
Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля и дифракция Фраунгофера. Дифракция от одной щели и от многих щелей. Спектральное разложение. Голография.
Основные формулы
· Радиус внешней границы k-й зоны Френеля:
a - расстояние диафрагмы с круглым отверстием от точечного источника света; b - расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; k - номер зоны Френеля; l - длина волны. Для плоской волны
· Дифракция Фраунгофера от щели; свет падает нормально. Условие минимумов интенсивности света
· Условие максимумов интенсивности света
· Дифракционная решетка, свет падает нормально. Условие главных максимумов интенсивности
d - период решетки; k - номер главного максимума; - угол между нормалью к поверхности решетки и направлением дифрагированных волн; · Условие добавочных минимумов
· Угловая дисперсия дифракционной решетки.
· Линейная дисперсия дифракционной решетки
· Для малых углов дифракции, угловая дисперсия:
где f - главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны. · Разрешающая способность дифракционной решетки
где N - число штрихов решетки. · Разрешающая сила объектива
где · Формула Вульфа-Брэгга. Условия дифракционных максимумов
d - межплоскостное расстояние;
Семестровые задания
24.1. На пластинку с щелью, ширина которой 24.2. На щель шириной 24.3. На щель шириной 24.4. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( 24.5. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол j1= 300. На какой угол j2 отклоняет она спектр четвертого порядка? 24.6. Расстояние между штрихами дифракционной решетки 24.7. Найти наибольший порядок k спектра для желтой линии натрия (l = =589нм), если постоянная дифракционной решетки 24.8. На дифракционную решетку нормально падает пучок света. Красная линия (l1 = 630 нм) видна в спектре третьего порядка под углом 600. Какая спектральная линия видна под этим же углом в спектре четвертого порядка? 24.9. Постоянная дифракционной решетки в 4 раза больше длины световой волны, падающей нормально на ее поверхность. Определить угол a между двумя первыми симметричными дифракционными максимумами. 24.10. На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую длину волны l2 в спектре третьего порядка накладывается красная линия гелия (l1 = 670 нм) спектра второго порядка? 24.11. На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница ( 24.12. Дифракционная картина наблюдается на расстоянии 24.13. Плоская световая волна падает нормально на диафрагму с круглым отверстием. В результате дифракции в некоторых точках отверстия, находящихся на расстоянии bi от его центра, наблюдаются максимумы интенсивности. 1. Получить вид функции b = f (k, l, r), где r - радиус отверстия, k - число зон Френеля, открываемых для данной точки оси отверстием. 2. Получить то же самое для точек оси отверстия, в которых наблюдаются минимумы интенсивности. 24.14. Плоская световая волна с длиной волны 24.15. Расстояние от точечного источника света ( 24.16. Определить радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 1,5 мм. 24.17. На диафрагму с круглым отверстием диаметром d = 5 мм падает нор-мально параллельный пучок света с длиной волны 24.18. Найти радиусы первых пяти зон Френеля, если расстояние от источника света до волновой поверхности a = 1м, расстояние от волновой поверхности до точки наблюдения b = 1 м. Длина волны света l = 0,5 мкм. 24.19.Найти радиусы первых пяти зон Френеля для плоской волны, если расстояние от волновой поверхности до точки наблюдения b = 1 м. Длина волны света l = 0,5 мкм. 24.20. При нормальном падении света на дифракционную решетку угол дифракции для линии
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.008 с.) |



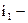 угол падения;
угол падения; 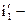 угол отражения;
угол отражения;  угол преломления;
угол преломления;  относительный показатель преломления второй среды относительно первой;
относительный показатель преломления второй среды относительно первой; 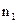 и
и  абсолютные показатели преломления первой и второй среды.
абсолютные показатели преломления первой и второй среды.

 соответственно расстояния от полюса зеркала до предмета и изображения;
соответственно расстояния от полюса зеркала до предмета и изображения; 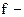 фокусное расстояние зеркала;
фокусное расстояние зеркала;  радиус кривизны зеркала.
радиус кривизны зеркала.
 относительный показатель преломления;
относительный показатель преломления; 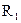 и
и  радиусы кривизны поверхностей (
радиусы кривизны поверхностей ( для выпуклой поверхности;
для выпуклой поверхности;  для вогнутой); а и
для вогнутой); а и  ,
, - световой поток, излучаемый источником в пределах телесного угла d
- световой поток, излучаемый источником в пределах телесного угла d 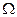 .
.
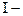 сила света источника.
сила света источника.
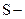 площадь этой поверхности.
площадь этой поверхности. светящейся поверхности в некотором направлении
светящейся поверхности в некотором направлении 
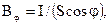
 угол между нормалью к элементу поверхности и направлением наблюдения.
угол между нормалью к элементу поверхности и направлением наблюдения.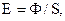
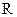 и яркости В при условии, что яркость не зависит от
и яркости В при условии, что яркость не зависит от
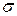 для луча, проходящего через призму с преломляющим углом
для луча, проходящего через призму с преломляющим углом 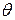 =200, если луч падает под углом 50. Показатель преломления вещества призмы n = 1,52.
=200, если луч падает под углом 50. Показатель преломления вещества призмы n = 1,52.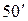 . Чему равна скорость распространения света в скипидаре.
. Чему равна скорость распространения света в скипидаре. ,
, ,
, - расстояние от источников до экрана наблюдения, d - расстояние между источниками.
- расстояние от источников до экрана наблюдения, d - расстояние между источниками. , или
, или (max)
(max) - l/2 = ± (2k + 1) l / 2,
- l/2 = ± (2k + 1) l / 2,

 =0,7 мкм.
=0,7 мкм. =0,003 рад на расстоянии l =1,9 м от экрана и d =
=0,003 рад на расстоянии l =1,9 м от экрана и d = =2 мм.
=2 мм. , k=1,2,3...
, k=1,2,3... .
.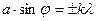 ,
, 
 - ширина щели;
- ширина щели;  - угол дифракции.
- угол дифракции. ,
,  - приближенное значение угла дифракции.
- приближенное значение угла дифракции. ,
, 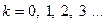
 ,
, 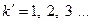 кроме 0, N, 2N...
кроме 0, N, 2N... .
. .
. ,
,
 ,
, - наименьшее угловое расстояние, разрешаемое объективом, D – его диаметр.
- наименьшее угловое расстояние, разрешаемое объективом, D – его диаметр. ,
,  - угол скольжения.
- угол скольжения. = 400 нм. На ре-шетку падает нормально свет с длиной волны l = 0,580 мкм. Максимум какого наибольшего порядка дает эта решетка?
= 400 нм. На ре-шетку падает нормально свет с длиной волны l = 0,580 мкм. Максимум какого наибольшего порядка дает эта решетка? мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает три зоны Френеля.
мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает три зоны Френеля. = 0,65 мкм во втором порядке равен 45o. Найти угол дифракции для линии
= 0,65 мкм во втором порядке равен 45o. Найти угол дифракции для линии 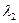 = 0,5 мкм в третьем порядке.
= 0,5 мкм в третьем порядке.


