Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Атом и Молекула водорода в квантовой теорииСодержание книги
Поиск на нашем сайте
Уравнение Шредингера для атома водорода. Водородоподобные атомы. Энергетические уровни. Ширина уровней в сложныхатомах. Принцип Паули. Молекула водорода.Ионная и ковалентная связи. Электронные термы двухатомной молекулы.
Основные формулы · Потенциальная энергия водородоподобном атоме:
где · Собственное значение энергии
· Энергия ионизации атома водорода
· Момент импульса (механический орбитальный момент) электрона
где · Проекция момента импульса на направление
где · Правила отбора для орбитального и магнитного квантовых чисел
· Нормированная волновая функция, отвечающая (основному состоянию n=1, l=0,m=0) электрона в атоме водорода,
где · Вероятность обнаружить электрон в атоме водорода, находящемся в
· Спин (собственный механический момент импульса) электрона
где · Коротковолновая граница сплошного рентгеновского спектра
где
характеристического рентгеновского излучения,
где
Семестровые задания
31.1. Написать уравнение Шредингера для электрона, находящегося в водородном атоме. 31.2. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
где 31.3. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
где 31.4. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
где 31.5. Определить с помощью уравнения Шредингера энергию электрона, находящегося в атоме водорода в состоянии 31.6. Волновая функция 31.7. Волновая функция, описывающая 1s – состояние электрона в атоме водорода, имеет вид 31.8. Собственная функция, описывающая основное состояние электрона в атоме водорода, имеет вид 31.9. Электрон в атоме водорода описывается в основном состоянии волновой функцией 31.10. Зная, что нормированная собственная волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид Глава VI. физика атомного ядра
Атомное ядро
Строение атомных ядер. Ядерные силы. Обменный характер ядерных сил. Модели ядра. Закономерности и происхождение альфа-, бета- и гамма-излучения и взаимодействиеих с веществом. Ядерные реакции. Радиоактивные превращения атомных ядер. Реакции ядерного деления. Цепная реакция деления. Ядерный реактор. Реакция синтеза. Проблема управляемой термоядерной реакции.
Основные формулы
где · Закон радиоактивного распада
где · Период полураспада
· Число атомов, распавшихся за время
· Среднее время жизни
· Число атомов, содержащихся в радиоактивном изотопе,
где · Активность
где · Если имеется смесь ряда радиоактивных изотопов, образующихся один из другого, и если постоянная распада
· Дефект массы ядра
где · Энергия связи ядра
где Во внесистемных единицах энергия связи ядра равна
Семестровые задания
32.1. Определить число N атомов радиоактивного препарата иода 32.2. Найти период полураспада Т1/2 радиоактивного изотопа, если его активность за время t = 10 суток уменьшилась на 24% по сравнению с перво-начальной. 32.3. Определить, какая доля радиоактивного изотопа 32.4. Найти активность Амассы m = 1 мкг полония 32.5. Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить активность этого изотопа по истечении промежутка времени, равного половине периода полураспада. 32.6. Начальная активность 1 г изотопа радия 32.7. Определить период полураспада Т1/2 некоторого радиоактивного изотопа, если его активность за 5 суток уменьшилась 2,2 раза. 32.8. Определить период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалась за время t=849 с. 32.9. Период полураспада радиоактивного изотопа актиния 32.10. Определить, какая часть начального количества ядер радиоактивного изотопа останется нераспавшейся по истечении времени t, равного трем средним временам жизни 32.11. Период полураспада радиоактивного изотопа составляет 24 ч. Опреде-лить время, за которое распадется 32.12. Определить сколько ядер m = 1 кг радиоактивного изотопа церия 32.13. Сколько атомов из N = 106 атомов полония распадается за время t=1 сут.? 32.14. Найти массу m радона, активность которого А = 3,7×1010 Бк. 32.15. Определить постоянную радиоактивного распада 32.16. Найти энергию, поглощенную при реакции
32.17. При бомбардировке изотопа азота 32.18. Определить удельную энергию связи для ядра 32.19. Какая энергия выделится, если при реакции 32.20. Определить энергию связи Есв/А (в МэВ), приходящуюся на один нуклон, для ядра 32.21. Определить энергию Q распада ядра углерода 32.22. Найти дефект массы и энергию связи ядра 32.23. Определить энергию, которая освободится при делении всех ядер, содержащихся в уране - 235 массой m = 1 г. (При делении одного ядра урана – 235 выделяется энергия Q = 200 МэВ). 32.24.Найти электрическую мощность Р атомной электростанции, расходующей 0,1 кг урана – 235 в сутки, если к.п.д. 32.25. Вычислить энергию связи Есв ядра дейтерия 32.26. Вычислить энергетический эффект Q реакции 32.27. Используя известные значения масс нейтральных атомов 32.28. Определить энергию Есв, которая освободится при соединении одного протона и двух нейтронов в атомное ядро. 32.29. Определить энергию связи Е ядра изотопа лития 32.30. Какую наименьшую энергию Е нужно затратить, чтобы разделить на отдельные нуклоны ядро 32.31. Какую наименьшую энергию Е нужно затратить, чтобы оторвать один нейтрон от ядра азота 32.32. Найти минимальную энергию связи Е, необходимую для удаления одного протона из ядра азота 32.33. Какую наименьшую энергию Е нужно затратить, чтобы разделить ядро 32.34. Определить наименьшую энергию Е, необходимую для разделения ядра углерода 32.35. Сколько ядер урана – 235 должно делиться в одну секунду, чтобы мощность ядерного реактора была равна 1 Вт? 32.36. Определить энергию, необходимую для разделения ядра 20Ne на две 32.37. В одном акте деления ядра урана 235U освобождается энергия 200 МэВ. Определить энергию, выделяющуюся при распаде всех ядер этого изотопа урана массой 32.38. Считая, что в одном акте деления ядра урана 235U освобождается энергия 200 МэВ, определить массу 32.39. Определить тепловой эффект следующей реакции: 32.40. Определить тепловой эффект следующей реакции:
ПРИЛОЖЕНИЯ Таблица 4
Основные физические постоянные (округленные значения)
____________ * Молярный объем идеального газа при нормальных условиях.
Таблица 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.107 (0.007 с.) |

 взаимодействия электрона с ядром в
взаимодействия электрона с ядром в
 расстояние между электроном и ядром;
расстояние между электроном и ядром;  порядковый номер элемента;
порядковый номер элемента;  электрическая постоянная.
электрическая постоянная. электрона в водородоподобном атоме
электрона в водородоподобном атоме


 ,
, орбитальное квантовое число, принимающее при заданном
орбитальное квантовое число, принимающее при заданном  следующие значения:
следующие значения:  (всего
(всего  внешнего магнитного поля
внешнего магнитного поля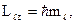
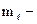 магнитное квантовое число, принимающее при заданном
магнитное квантовое число, принимающее при заданном  следующие значения:
следующие значения:  (всего
(всего  значений).
значений). 1 и
1 и 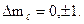
 состоянию
состоянию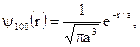
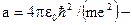 величина, совпадающая с первым боровским радиусом.
величина, совпадающая с первым боровским радиусом. до
до 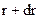
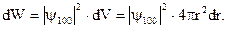

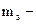 магнитное спиновое квантовое число
магнитное спиновое квантовое число 
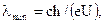
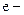 заряд электрона;
заряд электрона;  разность потенциалов, приложенная к рентгеновской трубке.
разность потенциалов, приложенная к рентгеновской трубке. Закон Мозли, определяющий частоты спектральных линий
Закон Мозли, определяющий частоты спектральных линий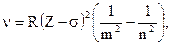
 постоянная Ридберга;
постоянная Ридберга;  постоянная экранирования;
постоянная экранирования; 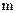 определяет рентгеновскую серию
определяет рентгеновскую серию 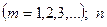 определяет линии соответствующей серии
определяет линии соответствующей серии  .
.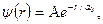
 — некоторая постоянная,
— некоторая постоянная,  — первый боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
— первый боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
 кулоновской силы.
кулоновской силы.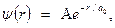
 потенциальной энергии.
потенциальной энергии. , где A, а и a - некоторые постоянные.
, где A, а и a - некоторые постоянные. определена только в области
определена только в области  . Используя условие нормировки, определить нормировочный множитель А.
. Используя условие нормировки, определить нормировочный множитель А. , где r – расстояние электрона от ядра, a0 – первый боровский радиус. Определить нормированную волновую функцию, отвечающую этому состоянию.
, где r – расстояние электрона от ядра, a0 – первый боровский радиус. Определить нормированную волновую функцию, отвечающую этому состоянию.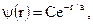 где
где  (боровский радиус). Определить расстояние
(боровский радиус). Определить расстояние 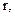 на котором вероятность нахождения электрона максимальна.
на котором вероятность нахождения электрона максимальна. Определить отношение вероятностей
Определить отношение вероятностей  пребывания электрона в сферических слоях толщиной
пребывания электрона в сферических слоях толщиной 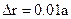 и радиусами
и радиусами  и
и 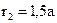 .
. найти среднее расстояние
найти среднее расстояние  электрона от ядра.
электрона от ядра.
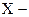 символ химического элемента;
символ химического элемента; 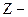 атомной номер (число протонов в ядре);
атомной номер (число протонов в ядре);  массовое число (число нуклонов в ядре). Число
массовое число (число нуклонов в ядре). Число  нейтронов в ядре равно разности
нейтронов в ядре равно разности  .
.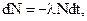 или
или 
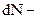 число ядер, распадающихся за интервал времени
число ядер, распадающихся за интервал времени 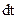 ;
;  число ядер, распадающихся к моменту времени
число ядер, распадающихся к моменту времени  ;
;  число ядер в начальный момент
число ядер в начальный момент 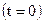 ;
;  постояная радиоактивного распада.
постояная радиоактивного распада. промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением:
промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением: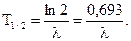

 радиоактивного ядра – промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:
радиоактивного ядра – промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:

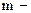 масса изотопа,
масса изотопа,  его молярная масса;
его молярная масса;  постоянная Авогадро.
постоянная Авогадро.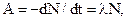 или
или 
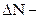 число ядер, распадающихся за интервал времени
число ядер, распадающихся за интервал времени  активность изотопа в начальный момент времени.
активность изотопа в начальный момент времени. первого члена ряда много меньше постоянных всех остальных членов ряда, то в смеси устанавливается состояние радиоактивного равновесия, при котором активности всех членов ряда равны между собой:
первого члена ряда много меньше постоянных всех остальных членов ряда, то в смеси устанавливается состояние радиоактивного равновесия, при котором активности всех членов ряда равны между собой: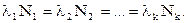
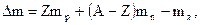
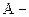 массовое число (число нуклонов в ядре);
массовое число (число нуклонов в ядре);  число нейтронов в ядре;
число нейтронов в ядре; 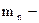 масса нейтрона;
масса нейтрона;  масса протона;
масса протона;  масса ядра.
масса ядра.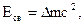
 дефект массы ядра;
дефект массы ядра; 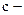 скорость света в вакууме.
скорость света в вакууме.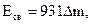 где дефект массы
где дефект массы  I массой 0,5 мкг, распавшихся в течение времени t = 7 суток.
I массой 0,5 мкг, распавшихся в течение времени t = 7 суток. распадается в течение времени t = 6 суток.
распадается в течение времени t = 6 суток. (период полураспада 138 суток)
(период полураспада 138 суток) Ао=3,7·1010 Бк. Опреде-лить период полураспада Т1/2 этого изотопа.
Ао=3,7·1010 Бк. Опреде-лить период полураспада Т1/2 этого изотопа. составляет 10сут. Определить время, за которое распадется 1/3 начального количества ядер актиния.
составляет 10сут. Определить время, за которое распадется 1/3 начального количества ядер актиния. радиоактивного ядра.
радиоактивного ядра.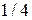 начального количества ядер.
начального количества ядер. распадается в течение времени
распадается в течение времени  с. Период полураспада церия Т1/2=285 сут.
с. Период полураспада церия Т1/2=285 сут. для
для 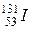 . Период полураспада изотопа иода равен 8 сут.
. Период полураспада изотопа иода равен 8 сут.
 нейтронами получается изотоп углерода
нейтронами получается изотоп углерода  , который оказывается
, который оказывается  - радиоактивным. Написать уравнения обеих реакций.
- радиоактивным. Написать уравнения обеих реакций.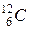 , если масса его нейтрального атома равна 19,9272·10-27 кг.
, если масса его нейтрального атома равна 19,9272·10-27 кг. подвергаются превращению все ядра, находящиеся в 1г алюминия
подвергаются превращению все ядра, находящиеся в 1г алюминия .
. , выбросившего позитрон и нейтрино.
, выбросившего позитрон и нейтрино.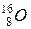 .
. станции равен 16%.
станции равен 16%.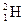 и трития
и трития 
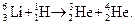
 и электрона, определить массы mp протона, md дейтона.
и электрона, определить массы mp протона, md дейтона. .
. ?
?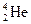 на две одинаковые части?
на две одинаковые части? на три одинаковые части.
на три одинаковые части.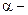 частицы и ядро 12С. Энергия связи на один нуклон в ядрах 20Ne,
частицы и ядро 12С. Энергия связи на один нуклон в ядрах 20Ne,  и 12С равны соответственно 8,03, 7,07 и 7,68 МэВ.
и 12С равны соответственно 8,03, 7,07 и 7,68 МэВ.