
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы механики сплошных сpeдСодержание книги
Поиск на нашем сайте
Понятие сплошной среды. Общие свойства жидкостей и газов. Идеальная и вязкая жидкость. Уравнение Бернулли. Ламинарное и турбулентное течения жидкостей. Формула Стокса. Формула Пуазейля. Упругие напряжения.
Основные формулы
· Гидростатическое давление столба жидкости на глубине
где · Закон Архимеда
где · Уравнение неразрывности
где · Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости
где · Формула Торичелли, позволяющая определить скорость истечения жидкости из малого отверстия в открытом широком сосуде,
где · Формула Пуазейля. Объем жидкости (газа), протекающий за время
где · Сила внутреннего трения между слоями текущей жидкости
где · Формула Стокса, позволяющая определить силу сопротивления, действующую на медленно движущийся в вязкой среде шарик,
где
Семестровые задания
5.1. В широком сосуде, наполненном глицерином ( 5.2. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии h1= 36 см от дна сосуда и на расстоянии h2= 9 см от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии 5.3. В высокий цилиндрический сосуд, наполненный глицерином, бросают алюминиевый шарик диаметром d = 6 мм. Определить, при какой скорости па-дение шарика станет равномерным. 5.4. Определить время истечения несжимаемой жидкости из открытого цилиндрического сосуда высотой H = 4,9 м, если диаметр небольшого отверстия в дне сосуда в 30 раз меньше диаметра сосуда. 5.5. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость 5.6. В широкой части горизонтально расположенной трубы нефть течет со скоростью 5.7. К поршню спринцовки, расположенной горизонтально, приложена сила F =15 H. Определить скорость 5.8. Давление р ветра, на стену равно 200 Па. Определить скорость 5.9. Бак высотой h = 1,5 м наполнен до краев водой. На расстоянии d = 1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии от бака падает на пол струя, вытекающая из отверстия? 5.10. Бак высотой Н = 2 м до краев заполнен жидкостью. На какой высоте h должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном от бака расстоянии? Гармонические колебания
Общие характеристики гармонических колебаний. Колебания груза на пружине, математический маятник, физический маятник. Сложение колебаний. Векторная диаграмма. Свободные затухающие колебания. Коэффициент затухания. Логарифмический декремент затухания. Вынужденные колебания под действием синусоидальной силы. Амплитуда и фаза при вынужденных колебаниях. Резонанс. Автоколебания.
Основные формулы
· Уравнение гармонических колебаний
где · Скорость и ускорение точки, совершающей гармонические колебания,
· Кинетическая энергия колеблющейся точки массой
· Потенциальная энергия
· Полная энергия
· Дифференциальное уравнение гармонических колебаний материальной точки массой
где · Период колебаний пружинного маятника
· Период колебаний физического маятника
где · Период колебаний математического маятника
где · Дифференциальное уравнение свободных затухающих колебаний линейной системы и его решение:
где · Декремент затухания
где · Логарифмический декремент затухания
где · Добротность колебательной системы
· Дифференциальное уравнение вынужденных колебаний и его решение для установившихся колебаний:
где
Семестровые задания
6.1. Полная энергия тела, совершающего гармоническое колебательное движение, равна 3×10-5 Дж, максимальная сила, действующая на тело, равна 1,5×10-3 Н. Написать уравнение движения этого тела, если период колебаний равен 2с и начальная фаза 600. 6.2. Амплитуда гармонических колебаний материальной точки А = 2 см, пол-ная энергия Е = 3×10-7Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25×10-5 Н? 6.3. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с2, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм. 6.4. Амплитуда гармонических колебаний равна 50 мм, период 4 с, начальная фаза 6.5. Материальная точка массой 10 г колеблется по уравнению x = Asin(wt+j), где А = 5 см, 6.6. Найти максимальную скорость и максимальное ускорение колеблющейся точки, если ее амплитуда 5 см, а период 4 с. 6.7. Определить период Т простых гармонических колебаний диска радиусом R = 50 см около горизонтальной оси, проходящей через образующую диска. 6.8. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение х0 = 4 см, а скорость 6.9. Определить частоту n простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости. 6.10. Определить потенциальную энергию П математического маятника с массой m = 20 г в положении, соответствующем углу отклонения нити от вертикали a = 100, если частота колебаний маятника n = 0,5 с-1. Потенциальную энергию маятника в положении равновесия считать равной нулю.
Волновые процессы
Основные характеристики волнового движения. Уравнение волны. Плоская синусоидальная волна. Бегущие и стоячие волны. Фазовая скорость. Эффект Доплера. Звук. Ультразвук.
Основные формулы
·Связь длины волны
где · Уравнение плоской волны, распространяющейся вдоль положительного направления оси x где x( · Связь между разностью фаз
· Условия максимума и минимума амплитуды при интерференции волн
где · Фазовая
· Уравнение стоячей волны
· Координаты пучностей и узлов
· Эффект Доплера в акустике
где
Семестровые задания
7.1. Задано уравнение плоской волны 7.2. Волна распространяется от источника колебаний вдоль прямой. Смещение точки для момента времени 0,5 Т составляет 5 см. Точка удалена от источника колебаний на расстояние 7.3. Источник совершает незатухающие колебания по закону 7.4. Звуковые колебания, имеющие частоту v = 0,5 кГц и амплитуду А = =0,25мм, распространяются в упругой среде. Длина волны 7.5. Определить разность фаз двух точек, отстоящих друг от друга на расстоянии 20 см, если волна распространяется со скоростью 7.6. От источника колебаний распространяется волна вдоль прямой линии. Амплитуда А колебаний равна 10 см. Как велико смещение точки, удаленной от источника на х = ¾ 7.7. Волна с периодом Т = 1,2 с и амплитудой колебаний А = 2 см распрост-раняется со скоростью 7.8. Две точки находятся на расстоянии х = 50 см друг от друга на прямой, вдоль которой распространяется волна со скоростью 7.9. Определить разность фаз 7.10. Волна распространяется в упругой среде со скоростью
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.008 с.) |


 ,
, - плотность жидкости.
- плотность жидкости. ,
, - выталкивающая сила;
- выталкивающая сила;  - объем вытесненной жидкости.
- объем вытесненной жидкости. ,
, - площадь поперечного сечения трубки тока;
- площадь поперечного сечения трубки тока;  - скорость жидкости.
- скорость жидкости.
 - статическое давление жидкости для определенного сечения трубки тока;
- статическое давление жидкости для определенного сечения трубки тока; 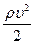 - динамическое давление жидкости для этого же сечения;
- динамическое давление жидкости для этого же сечения; 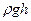 - гидростатическое давление.
- гидростатическое давление. ,
, через длинную трубку,
через длинную трубку, ,
, - радиус трубки;
- радиус трубки;  - ее длина;
- ее длина;  -разность давлений на концах трубки;
-разность давлений на концах трубки;  -динамическая вязкость (коэффициент внутреннего трения) жидкости.
-динамическая вязкость (коэффициент внутреннего трения) жидкости. ,
, - градиент скорости;
- градиент скорости;  ,
, г/см3), падает стеклянный шарик (
г/см3), падает стеклянный шарик ( г/см3) с постоянной скоростью. Диаметр шарика d = =1 мм. Определить динамическую вязкость глицерина.
г/см3) с постоянной скоростью. Диаметр шарика d = =1 мм. Определить динамическую вязкость глицерина. от сосуда струя воды падает на стол.
от сосуда струя воды падает на стол. воды в широкой части трубы равна 20 см/с. Определить скорость
воды в широкой части трубы равна 20 см/с. Определить скорость  , в узкой части трубы, диаметр
, в узкой части трубы, диаметр  которой в 1,5 раза меньше диаметра d1 широкой части.
которой в 1,5 раза меньше диаметра d1 широкой части. р давлений в широкой и узкой частях ее равна 6,65 кПа.
р давлений в широкой и узкой частях ее равна 6,65 кПа.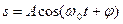 ,
, - смещение колеблющейся величины от положения равновесия; А- амплитуда колебаний;
- смещение колеблющейся величины от положения равновесия; А- амплитуда колебаний; 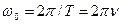 - круговая (циклическая) частота;
- круговая (циклическая) частота;  - частота; Т- период колебаний;
- частота; Т- период колебаний; 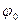 - начальная фаза.
- начальная фаза. ,
,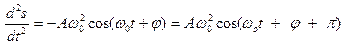 .
.
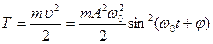 .
. .
. .
. или
или 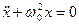 ,
, - коэффициент упругости (
- коэффициент упругости ( ).
).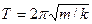 .
. ,
, - момент инерции маятника относительно оси колебаний;
- момент инерции маятника относительно оси колебаний;  - расстояние между точкой подвеса и центром масс маятника;
- расстояние между точкой подвеса и центром масс маятника;  -приведенная длина физического маятника;
-приведенная длина физического маятника;  - ускорение свободного падения.
- ускорение свободного падения. ,
, - длина маятника.
- длина маятника. ;
;  ,
, - коэффициент затухания (
- коэффициент затухания (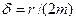 в случае механических колебаний и
в случае механических колебаний и  в случае электромагнитных колебаний);
в случае электромагнитных колебаний);  - циклическая частота свободных незатухающих колебаний той же колебательной системы;
- циклическая частота свободных незатухающих колебаний той же колебательной системы;  2- частота затухающих колебаний;
2- частота затухающих колебаний; 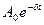 - амплитуда затухающих колебаний.
- амплитуда затухающих колебаний. ,
,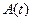 и
и 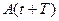 - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период.
- амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период. ,
, - время релаксации;
- время релаксации;  - число колебаний, совершаемых за время уменьшения амплитуды в
- число колебаний, совершаемых за время уменьшения амплитуды в  раз.
раз.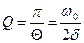 .
. ;
; 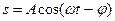 ,
, ).
). . Написать уравнение этого колебания. Найти смещение колеблющейся точки от положения равновесия при t = 0 и при t = 1,5 с.
. Написать уравнение этого колебания. Найти смещение колеблющейся точки от положения равновесия при t = 0 и при t = 1,5 с. . Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.
. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки. , периода
, периода  колебаний и частоты
колебаний и частоты 
 ;
;  ,
,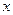 ,
,
 - смещение точек среды с координатой
- смещение точек среды с координатой  ; А- амплитуда волны;
; А- амплитуда волны; 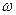 - циклическая (круговая) частота;
- циклическая (круговая) частота;  - волновое число (
- волновое число ( и разностью хода
и разностью хода 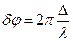 .
. ;
;  ,
,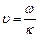 ;
; 
 .
. x(
x( .
. ;
; 
 .
. ,
, - частота звука, воспринимаемая движущимся приемником;
- частота звука, воспринимаемая движущимся приемником;  - частота звука, посылаемого источником;
- частота звука, посылаемого источником;  - скорость движения приемника;
- скорость движения приемника;  (х, t) = A cos (
(х, t) = A cos ( и ускорения
и ускорения  колебаний частиц среды.
колебаний частиц среды. . Определить амплитуду А колебаний.
. Определить амплитуду А колебаний. . Определить смещение точки, находящейся на расстоянии 0,6 см от источника колебаний, через t = 0,01 с после начала колебаний. Ско-рость распространения колебаний
. Определить смещение точки, находящейся на расстоянии 0,6 см от источника колебаний, через t = 0,01 с после начала колебаний. Ско-рость распространения колебаний 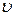 =300 м/с.
=300 м/с.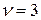 Гц.
Гц. колебаний в этих точках.
колебаний в этих точках. между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту v колебаний.
между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту v колебаний.


