
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корпускулярно-волновой дуализм микрообъектовСодержание книги
Поиск на нашем сайте СОДЕРЖАНИЕ • ЛЕКЦИЯ N 1 • Краткие исторические сведения. Тепловое излучение. Излучение абсолютно черного тела. Закон Кирхгофа. Итоги лекции N 1 • ЛЕКЦИЯ N 2 • Проблема излучения абсолютно черного тела. Формула Планка. Закон Стефана-Больцмана для энергетической светимости R(Т). Итоги лекции N 2 • ЛЕКЦИЯ N 3 • Проблема фотоэффекта. Уравнение Эйнштейна для фотоэффекта. Итоги лекции N 3 • ЛЕКЦИЯ N 4 • Боровская теория атома водорода. Спектры излучения атома водорода в теории Бора. Итоги лекции N 4 КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ МИКРООБЪЕКТОВ • ЛЕКЦИЯ N 5 • Свойства фотонов. Неделимость фотона. Интерференция одиночных фотонов. Вероятностная интерпретация плотности энергии и интенсивности электромагнитной волны. Итоги лекции N 5 • ЛЕКЦИЯ N 6 • Гипотеза де Бройля. Волновые свойства электронов. Дифракция единичных электронов. Волновая функция и волна де Бройля. Соотношения неопределенностей. Итоги лекции N 6 ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ • ЛЕКЦИЯ N 7 • Уравнение Шредингера. Понятия об операторах физических величин. Решение уравнения Шредингера для простейших случаев: свободная частица и частица в бесконечно глубокой одномерной потенциальной яме. Итоги лекции N 7 • ЛЕКЦИЯ N 8 • Уравнение Шредингера для атома водорода. Квантовые числа. Спектры атома водорода в теории Шредингера. Волновая функция основного состояния атома водорода. Итоги лекции N 8 • ЛЕКЦИЯ N 9 • Спин электрона. Принцип Паули. Фермионы и бозоны. Физические основы периодической системы элементов Д. И. Менделеева. Молекула. Объяснение температурной зависимости теплоемкостей газов. Итоги лекции N 9 КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ЭЛЕКТРОНОВ В МЕТАЛЛЕ • ЛЕКЦИЯ N 10 • Электронный газ в модели одномерной бесконечно глубокой ямы. Электронный газ в модели бесконечно глубокой трехмерной потенциальной ямы. Итоги лекции N 10 • ЛЕКЦИЯ N 11 • Электронный газ при Т > 0. Распределение Ферми-Дирака. Анализ функции f(E). Итоги лекции N 11 • ЛЕКЦИЯ N 12 • Результаты квантовой теории электропроводности металла. Термоэлектронная эмиссия. Бозоны. Распределение Бозе-Эйнштейна. Итоги лекции N 12 ВВЕДЕНИЕ В ТЕОРИЮ ТВЕРДЫХ ТЕЛ • ЛЕКЦИЯ N 13 • Происхождение энергетических зон в кристаллах. Металлы. Диэлектрики и полупроводники. Собственная проводимость полупроводников. Итоги лекции N 13 • ЛЕКЦИЯ N 14 • Примесная проводимость полупроводников. Акцепторные примеси. Полупроводники p-типа. Электронно-дырочный переход. Полупроводниковый диод. Полупроводниковый триод (транзистор). Итоги лекции N 14 ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ • ЛЕКЦИЯ N 15 • Вводные сведения. Вынужденное (стимулированное) излучение. Состояние с инверсией населенности. Оптический резонатор. Способы создания инверсии населенности. Виды лазеров и их применение. Итоги лекции N 15 ЭЛЕМЕНТЫ ФИЗИКИ ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ • ЛЕКЦИЯ N 16 • Размер, состав и заряд атомного ядра. Массовое и зарядовое число. Дефект масс и энергия связи атомного ядра. Ядерные силы. Итоги лекции N 16 • ЛЕКЦИЯ N 17 • Некоторые сведения из истории открытия деления ядра урана. Цепная ядерная реакция. Ядерная бомба. Ядерный реактор. Реакция синтеза атомных ядер. Проблема управляемых термоядерных реакций. Итоги лекции N 17 • ЛЕКЦИЯ N 18 • Радиоактивность. Историческое введение. Закон радиоактивного распада. Взаимодействие радиоактивного излучения с веществом. Методы регистрации ионизирующих излучений. Итоги лекции N 18 Тепловое излучение Излучение телами электромагнитных волн может происходить за счет различных видов энергии. Тепловым называется электромагнитное излучение, испускаемое веществом и возникающее за счет его внутренней энергии (см. Ч. 4, лекция N 4, § 2). Все остальные виды излучения, возбуждаемые внешними источниками энергии, называются люминесценцией. Тепловое излучение является единственным видом излучения, которое может находиться в термодинамическом равновесии с окружающими телами. Это обусловлено тем, что с повышением температуры тел интенсивность теплового излучения растет. Энергетическая светимость тела - это отношение энергии dE, испускаемой за время dt поверхностью dS излучающего тела по всем направлениям к величинам dS и dt:
По существу энергетическая светимость совпадает с интенсивностью излучения - средним по времени от вектора Пойнтинга, дающим плотность потока энергии электромагнитной волны. При тепловом излучении энергетическая светимость R является функцией температуры T. Спектральная плотность энергетической светимости rλ (или испускательная способность тела) - это отношение энергетической светимости dR, взятой в бесконечно малом интервале длин волн dλ, к величине dλ:
Спектральная плотность энергетической светимости rλ является функцией длины волны λ и температуры Т. Другое название rλ - испускательная способность. Из (1.6) получим, что
значит
Электромагнитное излучение можно характеризовать частотой ω и ввести спектральную плотность энергетической светимости rω. Спектральная плотность энергетической светимости rω - это отношение энергетической светимости dR, взятой в бесконечно малом интервале частот dω, к величине dω, т.е.:
rω является функцией частоты ω и температуры Т. Величину rω называют, также как и rλ, испускательной способностью тела. Величину rω чаще используют в теоретических исследованиях, а rλ - в экспериментальных. Из (1.9) получим, что:
значит
Величины λ и ω, как мы знаем, связаны соотношением λ = 2πc/ω (для электромагнитной волны в вакууме v = c). Связь dλ и dω получим дифференцированием этого равенства:
Знак "минус" указывает на то, что с ростом длины волны λ, круговая частота ω убывает. Для соответствующих интервалов dλ и dω можно записать:
Заменив dλ на его выражения через dω и опуская знак "минус", получим:
Используя эти выражения можно перейти от rλ к rω и обратно. Поток излучения Ф - это отношение энергии dЕ, переносимой электромагнитным излучением через какую-либо поверхность ко времени переноса dt, значительно превышающему период электромагнитных колебаний. Поток излучения Ф - синоним понятия мощность излучения. Единица измерения потока - ватт.
Поглощательная способность тела a ω - это отношение поглощаемого телом потока излучения dФω' (или dФλ') в интервале частот dω (или длин волн dλ) к падающему на него потоку dФω (или dФλ) в том же интервале dω (или dλ), т.е.:
Поглощательная способность тела a ω (как и a λ) - величины безразмерные (это следует из определения). Итоги лекции N 1 1. Немецкий физик Макс Планк в 1900 г. выдвинул гипотезу, согласно которой электромагнитная энергия излучается порциями, квантами энергии. Величина кванта энергии (см. (1.2): ε = h v, где h=6,6261·10-34 Дж·с - постоянная Планка, v - частота колебаний электромагнитной волны, излучаемой телом. Эта гипотеза позволила Планку решить проблему излучения абсолютно черного тела. 2. А Эйнштейн, развивая понятие Планка о квантах энергии ввел в 1905 г. понятие "квант света" или фотон. Согласно Эйнштейну квант электромагнитной энергии ε = h v движется в виде фотона, локализованного в малой области пространства. Представление о фотонах позволило Эйнштейну решить проблему фотоэффекта. 3. Английский физик Э. Резерфорд, основываясь на экспериментальных исследованиях, проведенных в 1909-1910 гг., построил планетарную модель атома. Согласно этой модели в центре атома расположено очень маленькое ядро (rя ~ 10-15 м), в котором сосредоточена почти вся масса атома. Заряд ядра положителен. Отрицательно заряженные электроны движутся вокруг ядра наподобие планет солнечной системы по орбитам, размер которых ~ 10-10 м. 4. Атом в модели Резерфорда оказался неустойчивым: согласно электродинамике Максвелла электроны, двигаясь по круговым орбитам, должны непрерывно излучать энергию, в результате чего за время ~ 10-8 с они должны упасть на ядро. Но весь наш опыт свидетельствует о стабильности атома. Так возникла проблема стабильности атома. 5. Решил проблему стабильности атома в 1913 г. датский физик Нильс Бор на основе выдвинутых им двух постулатов. В теории атома водорода, развитой Н. Бором, существенную роль играет постоянная Планка. 6. Тепловым называется электромагнитное излучение, испускаемое веществом за счет его внутренней энергии. Тепловое излучение может находиться в термодинамическом равновесии с окружающими телами. 7. Энергетическая светимость тела R - это отношение энергии dE, испускаемой за время dt поверхностью dS по всем направлениям, к dt и dS (см. (1.5)):
8. Спектральная плотность энергетической светимости rλ (или испускательная способность тела) - это отношение энергетической светимости dR, взятой в бесконечно малом интервале длин волн dλ, к величине dλ (см. (1.6)):
9. Поток излучения Ф - это отношение энергии dЕ, переносимой электромагнитным излучением через какую-либо поверхность ко времени переноса dt, значительно превышающему период электромагнитных колебаний (см. (1.13)):
10. Поглощательная способность тела aλ - это отношение поглощаемого телом потока излучения dФλ' в интервале длин волн dλ к падающему на него потоку dФλ в том же интервале dλ, (см. (1.14):
11. Абсолютно черное тело - это тело, для которого поглощательная способность тождественно равна единице для всех длин волн и для любой температуры, т.е.
Абсолютно черное тело - это модельное понятие. 12. Закон Кирхгофа утверждает, что отношение испускательной способности тела rλ к его поглощательной способности аλ одинаково для всех тел и является универсальной функцией длины волны λ (или частоты ω) и температуры Т (см. (1.17)):
ЛЕКЦИЯ N 2 Проблема излучения абсолютно черного тела. Формула Планка. Закон Стефана-Больцмана, закон Вина § 1. Проблема излучения абсолютно черного тела. Формула Планка Проблема излучения абсолютно черного тела состояла в том, чтобы теоретически получить зависимость φ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела. Казалось, что ситуация ясна: при заданной температуре Т молекулы вещества излучающей полости имеют максвелловское распределение по скоростям и излучают электромагнитные волны в соответствии с законами классической электродинамики. Излучение находится в термодинамическом равновесии с веществом, значит для нахождения спектральной плотности энергии излучения u(λ,T) и связанной с ней функции φ(λ,Т) можно использовать законы термодинамики и классической статистики. Однако, все попытки теоретиков получить на основе классической физики закон излучения абсолютно черного тела потерпели неудачу. Частичный вклад в решение этой проблемы внесли Густав Кирхгоф, Вильгельм Вин, Иозеф Стефан, Людвиг Больцман, Джон Уильям Релей, Джеймс Хонвуд Джинс. Проблема излучения абсолютно черного тела была решена Максом Планком. Для этого ему пришлось отказаться от классических представлений и сделать предположение о том, что заряд, совершающий колебания с частотой v, может получать или отдавать энергию порциями, или квантами. Величина кванта энергии в соответствии с (1.2) и (1.4):
где h - постоянная Планка; На основе представления о квантах энергии М. Планк, используя методы статистической термодинамики, получил выражение для функции u(ω,Т), дающей распределение плотности энергии в спектре излучения абсолютного черного тела:
Вывод этой формулы будет дан в лекции N 12, § 3 после того, как мы познакомимся с основами квантовой статистики. Для перехода к спектральной плотности энергетической светимости f(ω,Т) запишем вторую формулу (1.19):
Используя это соотношение и формулу Планка (2.1) для u(ω,T), получим, что:
Это и есть формула Планка для спектральной плотности энергетической светимости f( ω ,T). Теперь мы получим формулу Планка для φ(λ,Т).Как мы знаем из (1.18), в случае абсолютно черного тела f(ω,T) = rω, а φ(λ,Т) = rλ. Связь между rλ и rω дает формула (1.12), применяя ее мы получим:
Здесь мы аргумент ω функции f(ω,Т) выразили через длину волны λ. Подставляя сюда формулу Планка для f(ω,Т)из (2.2), получим формулу Планка для φ(λ,Т) - спектральной плотности энергетической светимости в зависимости от длины волны λ:
График этой функции хорошо совпадает с экспериментальными графиками φ(λ,Т) для всех длин волн и температур. Это и означает, что проблем излучения абсолютно черного тела решена. § 2. Закон Стефана-Больцмана и закон Вина Из (1.11) для абсолютно черного тела, когда rω = f(λ,Т), получим энергетическую светимость R(T), интегрируя функцию f(ω,Т) (2.2) во всем интервале частот.
Интегрирование дает:
Введем обозначение:
тогда выражение для энергетической светимости R примет следующий вид:
Это и есть закон Стефана-Больцмана. М. Стефан на основе анализа опытных данных пришел в 1879 г. к выводу, что энергетическая светимость любого тела пропорциональна четвертой степени температуры. Л. Больцман в 1884 г. нашел из термодинамических соображений, что такая зависимость энергетической светимости от температуры справедлива лишь для абсолютно черного тела. Постоянная σ носит название постоянной Стефана-Больцмана. Ее экспериментальное значение:
Вычисления по теоретической формуле дают для σ результат очень хорошо согласующийся с экспериментальным. Отметим, что графически энергетическая светимость равна площади, ограниченной графиком функции f(ω,Т), это иллюстрирует рисунок 2.1.
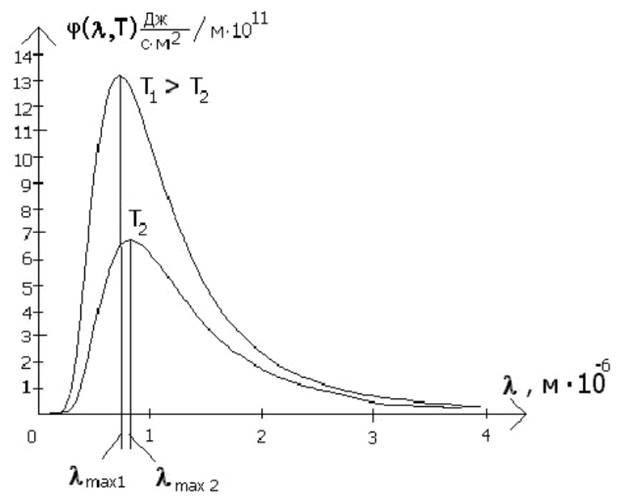
Рис. 2.1 Максимум графика спектральной плотности энергетической светимости φ(λ,Т) при повышении температуры смещается в область более коротких волн (рис. 2.2). Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум. Определив положение этого максимума, мы получим закон его перемещения с изменением температуры.
Рис. 2.2 Как известно из математики, для исследования функции на максимум надо найти ее производную и приравнять к нулю:
Подставив сюда φ(λ,Т) из (1.23) и взяв производную, получим три корня алгебраического уравнения относительно переменной λ. Два из них (λ = 0 и λ = ∞) соответствуют нулевым минимумам функции φ(λ,Т). Для третьего корня получается приближенное выражение:
Введем обозначение:
тогда положение максимума функции φ(λ,Т) будет определятся простой формулой:
Это и есть закон смещения Вина. Он назван так в честь В. Вина, теоретически получившим в 1894 г. это соотношение. Постоянная в законе смещения Вина имеет следующее численное значение:
Итоги лекции N 2 1. Проблема излучения абсолютно черного тела состояла в том, что все попытки получить на основе классической физики зависимость φ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела потерпели неудачу. 2. Эту проблему решил в 1900 г. М. Планк на основе своей гипотезы квантов: заряд, совершающий колебания с частотой v, может получить или отдавать энергию порциями или квантами. Величина кванта энергии:
здесь h = 6,626 ·10-34 - постоянная Планка, величина 3. Формула Планка для спектральной плотности энергетической светимости абсолютно черного тела имеет следующий вид (см. (2.4):
здесь λ - длина волны электромагнитного излучения, Т - абсолютная температура, h - постоянная Планка, с - скорость света в вакууме, k - постоянная Больцмана. 4. Из формулы Планка следует выражение для энергетической светимости R абсолютно черного тела:
которое позволяет теоретически вычислить постоянную Стефана-Больцмана (см. (2.5)):
теоретическое значение которой хорошо совпадает с ее экспериментальным значением:
в законе Стефана-Больцмана (см.(2.6)):
5. Из формулы Планка следует закон смещения Вина, определяющий λmax - положение максимума функции φ(λ,Т) в зависимости от абсолютной температуры (см. (2.9):
Для b - постоянной Вина - из формулы Планка получается следующее выражение (см. (2.8)):
Постоянная Вина имеет следующее значение b = 2,90 ·10-3 м·К.
ЛЕКЦИЯ N 3 Проблема фотоэффекта. Уравнение Эйнштейна для фотоэффекта § 1. Проблема фотоэффект а Фотоэффект - это испускание электронов веществом под действием электромагнитного излучения. Такой фотоэффект называют внешним. Именно о нем мы будем говорить в этой главе. Есть еще и внутренний фотоэффект. (см. лекцию 13, § 2). В 1887 г. немецкий физик Генрих Герц обнаружил, что ультрафиолетовый свет, освещающий отрицательный электрод в разряднике, облегчает прохождение разряда. В 1888-89 гг. русский физик А. Г. Столетов занимается систематическим исследованием фотоэффекта (схема его установки приведена на рисунке). Исследования проводились в атмосфере газа, что сильно усложняло происходившие процессы.
Рис. 3.1 Столетов обнаружил, что: 1) наибольшее воздействие оказывают ультрафиолетовые лучи; 2) сила тока возрастает с увеличением интенсивности света, освещающего фотокатод; 3) испущенные под действием света заряды имеют отрицательный знак. Дальнейшие исследования фотоэффекта производились в 1900-1904 гг. немецким физиком Ф. Ленардом в наивысшем достигнутом в то время вакууме. Ленарду удалось установить, что скорость вылетающих из фотокатода электронов не зависит от интенсивности света и прямо пропорционально его частоте. Так родилась проблема фотоэффекта. Объяснить результаты опытов Ленарда на основе электродинамики Максвелла было невозможно! На рисунке 3.2 изображена установка, позволяющая детально изучать фотоэффект.
Рис. 3.2 Электроды, фотокатод и анод, помещены в баллон, из которого откачан воздух. Свет на фотокатод подается через кварцевое окошко. Кварц, в отличие от стекла, хорошо пропускает ультрафиолетовые лучи. Разность потенциалов (напряжение) между фотокатодом и анодом измеряет вольтметр. Ток в цепи анода измеряется чувствительным микроамперметром. Для регулировки напряжения батарея питания подключена к реостату со средней точкой. Если движок реостата стоит против средней точки, подсоединенной через микроамперметр к аноду, то разность потенциалов между фотокатодом и анодом равна нулю. При смещении движка влево, потенциал анода становится отрицательным относительно катода. Если движок реостата сдвигать вправо от средней точки, то потенциал анода становится положительным. Вольт-амперная характеристика установки по изучению фотоэффекта позволяет получить информацию об энергии электронов, испускаемых фотокатодом. Вольт-амперная характеристика - это зависимость фототока i от напряжения между катодом и анодом U. При освещении светом, частота v которого достаточна для возникновения фотоэффекта, вольт-амперная характеристика имеет вид графика, изображенного на рис. 3.3:
Рис. 3.3 Из этой характеристики следует, что при некотором положительном напряжении на аноде фототок i достигает насыщения. При этом все электроны, испущенные фотокатодом в единицу времени, попадают за это же время на анод. При U = 0 часть электронов долетает до анода и создает фототок i0. При некотором отрицательном напряжении на аноде - Uзад - фототок прекращается. При этом значении напряжения максимальная кинетическая энергия фотоэлектрона у фотокатода (mv2max)/2 полностью расходуется на совершение работы против сил электрического поля:
В этой формуле me - масса электрона; vmax - его максимальная скорость у фотокатода; e - абсолютное значение заряда электрона. Таким образом, измерив задерживающее напряжение Uзад, можно найти кинетическую энергию (и скорость электрона) сразу после его вылета из фотокатода. Опыт показал, что 1) энергия вылетевших из фотокатода электронов (и их скорость) не зависела от интенсивности света! При изменении частоты света v меняется и Uзад, т.е. максимальная кинетическая энергия электронов, покидающих фотокатод; 2) максимальная кинетическая энергия электронов, у фотокатода, (mv2max)/2, прямо пропорциональна частоте v света, освещающего фотокатод. Проблема, как и в случае с излучением абсолютно черного тела, состояла в том, что теоретические предсказания, сделанные для фотоэффекта на основе классической физики (электродинамики Максвелла), противоречили результатам опытов. Интенсивность света I в классической электродинамике является плотностью потока энергии световой волны. Во-первых, с этой точки зрения, энергия, передаваемая световой волной электрону, должна быть пропорциональна интенсивности света. Опыт не подтверждает это предсказание. Во-вторых, в классической электродинамике нет никаких объяснений прямой пропорциональности кинетической энергии электронов, (mv2max)/2, частоте света v. Итоги лекции N 3 1. Фотоэффект - это испускание электронов веществом под действием электромагнитного излучения. 2. Экспериментальные исследования фотоэффекта, приведенного в 1900-1904 гг., показали, что 1) энергия вылетевших из фотокатода электронов не зависит от интенсивности света; 2) эта энергия прямо пропорциональна частоте v света, освещающего фотокатод. 3. Проблема фотоэффекта состояла в том, что теоретические предсказания, сделанные для фотоэффекта на основе электродинамики Максвелла, противоречили результатам опытов. Теория Максвелла предсказывала, что энергия, передаваемая световой волной электрону, должна быть пропорциональна интенсивности света. Кроме того, в классической электродинамике нет никаких объяснений прямой пропорциональности кинетической энергии электронов (mv2max)/2 частоте света v. 4. Проблема фотоэффекта была разрешена в 1905 г. А. Эйнштейном, который предположил, что свет состоит из потока фотонов с энергией (см. (3.2)):
5. Применив к процессу поглощения фотона закон сохранения энергии, Эйнштейн получил следующее уравнение для фотоэффекта (см. (3.3)):
здесь А - работа выхода электрона из вещества, m - масса электрона, vmax - его скорость в момент вылета из фотокатода. 6. Из уравнения Эйнштейна для фотоэффекта следует, что, если энергия фототока h v меньше работы выхода А, то фотоэффект невозможен. Граничная частота называется красной границей фотоэффекта и определяется равенством (см. (3.5)):
ЛЕКЦИЯ N 4 Итоги лекции N 4 1. Уравнение движения электрона в планетарной модели атома, записанное на основе второго закона Ньютона, позволяет атому иметь любой размер, опыт же показывает, что размеры атомов порядка 10-10 м. Это противоречие теории и опыта получило название проблемы размера атома. 2. Проблема стабильности атома состояла в том, что в планетарной модели атома электрон, двигаясь по окружности, должен, из-за наличия ускорения, непрерывно излучать энергию и через время ~10-8 с упасть на ядро. Однако, весь наш опыт весомо свидетельствует о стабильности атомов. 3. Проблемы эти были решены в 1913 г. Н. Бором на основе его двух постулатов: 1) существуют стационарные состояния атом, находясь в которых он не излучает электромагнитных волн. Условие стационарности состояния атома - квантование момента импульса электрона L:
2) излучение испускается или поглощается в виде квантов энергии
здесь Еn - энергия стационарного состояния до перехода, Еm - энергия стационарного состояния после перехода. 4. Дополнив механику Ньютона этими постулатами, Н. Бор получил выражения для радиусов стационарных орбит rn (см. (4.5)):
и энергии стационарных состояний атома водорода Еn (см. (4.8)):
В этих формулах n - целое положительное число: n = 1, 2, 3... 5. Из второго постулата Бора и формулы для Еn следует выражение, определяющее длины волн, излучаемых (и поглощаемых) атомом водорода (см. (4.12), (4.13)):
R' называют постоянной Ридберга, ее экспериментальное значение
Величину R также называют постоянной Ридбера, теория Бора дает для нее следующее выражение:
Теоретическое значение R близко к ее экспериментальному значению. R = 3,29 · 1015 1/c.
ЛЕКЦИЯ N 5 Свойства фотонов Фотон - это элементарная частица, квант электромагнитного излучения. 1. Скорость фотона всегда постоянна и равна скорости света в вакууме.
Масса фотона
Энергия фотона
4. Импульс фотона
здесь k = ω/c - волновое число; Выражения для импульса фотона следует из релятивистского инварианта с учетом того, что масса фотона mγ = 0. В самом деле, из (Ч. 1, (12.9)) для фотона с энергией ε имеем:
Так как для фотона m ≡ mγ = 0, то
Неделимость фотона Фотон частоты ω всегда регистрируется как частица, несущая энергию. Нельзя получить фотоны той же самой частоты ω, но с энергией ε' = ε/2! Рассмотрим мысленный опыт с полупрозрачным зеркалом, разделяющим пучок света интенсивностью I на две части, интенсивностью I /2 каждая. Схема этого мысленного опыта изображена на рисунке 5.1.
Рис. 5.1 Предположим, что сначала интенсивность света I велика. Тогда по величине фототока i фотоэлементов 1 и 2 можно судить об интенсивностях пучков I1 и I2. Такой опыт можно проделать реально и убедиться в том, что наше полупрозрачное зеркало действительно делит интенсивный пучок пополам. Разумеется надо подобрать фотоэлемент с работой выхода Теперь изменим условие опыта. Пусть интенсивность пучка, идущего от источника света, так мала, что фотоны проходят через нашу установку поодиночке. Пусть соотношение между работой выхода и энергией фотона удовлетворяет еще одному условию:
Рис. 5.2 Как видно на изображенной энергетической схеме фотоэффекта, целый фотон с энергией ε вызовет фотоэффект и фотоэлемент сработает Первый вариант: каждый фотон делится пополам, так что после полупрозрачного зеркала энергия разделенных фотонов ε' = ε/2. Тогда фотоэлементы 1 и 2 перестают срабатывать. Но, если в этом случае убрать полупрозрачное зеркало, то целые фотоны с энергией Второй вариант: фотон не делится зеркалом пополам, а либо целиком попадает на фотоэлемент 1, либо, целиком же, попадает на фотоэлемент 2, заставляя их срабатывать попеременно. Реальные опыты с фотонами показывают, что в действительности осуществляется второй вариант: фотон неделим! Итоги лекции N 5 1. Корпускулярно-волновой дуализм микрообъектов заключается в том, что всем им (фотонам, электронам, протонам, нейтронам и т.д.) присущи одновременно и корпускулярные и волновые свойства. 2. Фотон - это элементарная частицы, квант электромагнитного излучения. Он обладает следующими свойствами:
3. Распространение фотонов в пространстве в некотором смысле правильно описывается уравнениями Максвелла для электромагнитных волн, при этом величины плотности энергии электромагнитной волны в вакууме:
и интенсивности I ~ E2 - для одиночных фотонов определяют вероятность обнаружить фотон в некоторой области пространства.
ЛЕКЦИЯ N 6 ЛЕКЦИЯ N 6 Итоги лекции N 6 1. Гипотеза о наличии у электронов волновых свойств выдвинул в 1924 году Л. де Бройль. В соответствии с этой гипотезой длина волны де Бройля λ определяется формулой:
где р - импульс электрона. Частота волны де Бройля находится из формулы:
где Е - энергия электрона. 2. Длины волн де Бройля для макроскопических объектов чрезвычайно малы, поэтому их волновые свойства (интерференция и дифракция) не проявляются. 3. Волновые свойства электронов обнаружили в 1927 г. Дэвиссон и Джермер в эксперименте по отражению электронов от поверхности кристалла никеля. 4. Советские физики А.М. Биберман, Н.Г. Сушкин и В.А. Фабрикант выполнили в 1949 г. опыты по дифракции одиночных электронов. При этом с течением времени формировалась такая же дифракционная картина, как и при большой интенсивности пучка. Из этих опытов следует, что каждому одиночному электрону присущи наряду с корпускулярными и волновые свойства. 5. Волна де Бройля является частным случаем более общего фундаментального понятия квантовой физики волновой функции. Ее принято обозначать греческой буквой Ψ, ("пси"). 6. Физический смысл волновой функции состоит в том, что квадрат ее модуля определяет вероятность dw того, что микрообъект будет обнаружен в пределах объема dV (см. (6.3)):
Эту вероятностную интерпретацию дал волновой функции в 1926 г. Макс Борн. 7. Соотношение неопределенностей утверждает, что произведение неопределенности координаты микрочастицы на неопределенность ее импульса не может быть меньше, чем
аналогичные соотношения справедливы для Δy Δpy и ΔzΔpz. Эти соотношения были установлены в 1927 г. В. Гейзенбергом и носят его имя: соотношения неопределенностей Гейзенберга.
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ ЛЕКЦИЯ N 7 Уравнение Шредингера Волновое уравнение, позволяющее найти волновую функцию частицы, которая движется в заданном силовом поле, имеет следующий вид:
здесь
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |


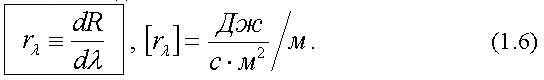


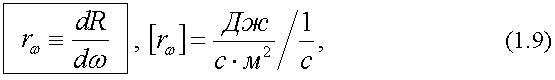



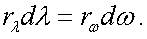



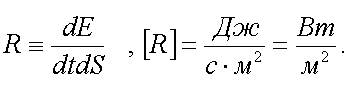



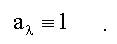


 v - частота колебаний электромагнитной волны, излученной колеблющемся зарядом; ω = 2π v - круговая частота.
v - частота колебаний электромагнитной волны, излученной колеблющемся зарядом; ω = 2π v - круговая частота.








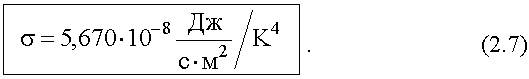

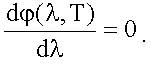




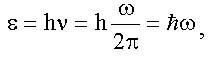
 Дж·с также называется постоянной Планка ["аш" с чертой], ω - круговая (циклическая) частота.
Дж·с также называется постоянной Планка ["аш" с чертой], ω - круговая (циклическая) частота.

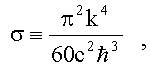








 .
.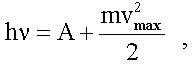

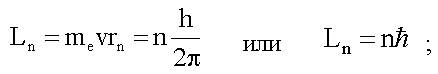
 при переходе электрона из одного стационарного состояния в другое. Энергия кванта равна разности энергий стационарных состояний атома, между которыми происходит переход:
при переходе электрона из одного стационарного состояния в другое. Энергия кванта равна разности энергий стационарных состояний атома, между которыми происходит переход:
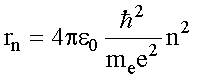
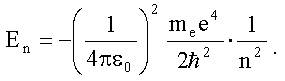


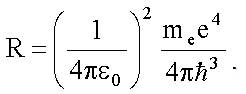


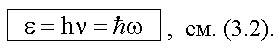


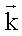 - волновой вектор.
- волновой вектор.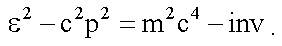
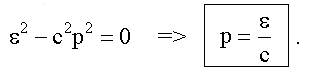

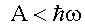 , это условие необходимо для наблюдения фотоэффекта.
, это условие необходимо для наблюдения фотоэффекта.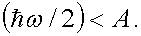 Вместе с предыдущим условием мы имеем:
Вместе с предыдущим условием мы имеем: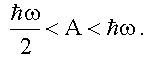
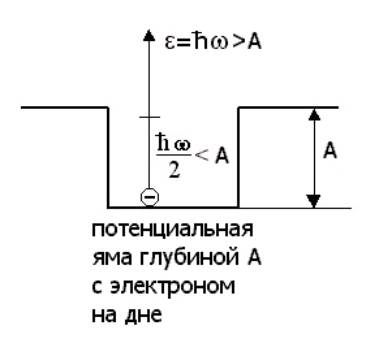
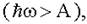 половина же фотона не сможет заставить сработать фотоэлемент
половина же фотона не сможет заставить сработать фотоэлемент  Логически при прохождении одиночных фотонов возможны два варианта.
Логически при прохождении одиночных фотонов возможны два варианта.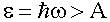 попадут на фотоэлемент 1 и он будет срабатывать.
попадут на фотоэлемент 1 и он будет срабатывать.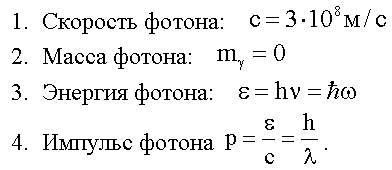
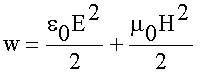
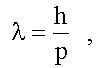


 , т.е.
, т.е.

 - постоянная Планка; m - масса частицы; U - ее потенциальная энергия во внешнем поле, которая, вообще говоря, может зависеть и от времени t,
- постоянная Планка; m - масса частицы; U - ее потенциальная энергия во внешнем поле, которая, вообще говоря, может зависеть и от времени t,  - мнимая единица, через
- мнимая единица, через  обозначен оператор Лапласа. Оператор - это совокупность действий, которые над
обозначен оператор Лапласа. Оператор - это совокупность действий, которые над 


