
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнения Шредингера для простейших случаев: свободная частица и частица в бесконечно глубокой одномерной потенциальной ямеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для свободной частицы потенциальная энергия U ≡ 0. Уравнение Шредингера (7.3) в этом случае выглядит следующим образом:
Для частицы, движущейся вдоль оси х, волновая функция ψ = ψ(х) и уравнение еще упрощается:
Решением этого уравнения будет экспоненциальная функция:
проверить это легко прямой подстановкой. При этом для энергии E получаем, как и следовало ожидать,
здесь px = mv - импульс частицы. Мы видим, что у свободной частицы энергия E и импульс px могут принимать любые значения, т.е. не квантуются. Полную волновую функцию Ψ(x, t) получим, домножив ψ(x) на временной множитель (см. (28.1)):
Это есть не что иное, как уравнение волны де Бройля (6.2). В случае бесконечно глубокой одномерной потенциальной ямы шириной а потенциальная энергия:
Изобразим график U(x) (см. рис. 7.1). Если частица находится в яме, то ее координата х может изменяться от нуля до a. За пределы ямы частица выйти не может, т.к. там потенциальная энергия бесконечно велика (стенки ямы бесконечно высоки). Значит вероятность обнаружить частицу в любом месте за пределами ямы равна нулю (dw = 0).
Рис. 7.1 В одномерном случае из (6.3) получим:
Откуда следует, что за пределами ямы волновая функция ψ тождественно обращается в ноль. Из условия непрерывности волновой функции следует, что внутри ямы она должна так зависеть от координаты х, чтобы обращаться в ноль на границах ямы. Значит граничные условия на волновую функцию ψ будут иметь следующий вид:
Внутри ямы U ≡ 0 и уравнение Шредингера будет иметь такой же вид, как и для свободной частицы (7.10):
или
Так как E = p2/2m, то для коэффициента при ψ имеем:
Откуда энергия частицы:
Здесь В результате уравнение Шредингера примет вид хорошо известного нам дифференциального уравнения:
Решением этого уравнения, как известно, являются гармонические функции (синус или косинус) и мнимая экспонента. Здесь нам удобнее взять функцию "синус" с нулевой начальной фазой. Тогда ψ(x) - волновая функция частицы, будет иметь следующий вид:
Постоянная С будет найдена позднее из условия нормировки (7.14). Т.к. sin 0 = 0, то граничное условие на левой границе (ψ(0) = 0) автоматически выполняется. Потребуем выполнения граничного условия на правой границе:
Это граничное условие будет выполнено, если
Значение целого числа n = 0 хотя и удовлетворяет граничному условию, но оно тождественно обращает волновую функцию в ноль (отсутствие частицы в яме!) и поэтому не годится. Отрицательные значения n не приводят к появлению новых состояний: при изменении знака n меняется знак ψ, тогда как вероятность В результате мы получили, что вследствие граничных условий волновое число k может принимать лишь дискретные значения:
где квантовое число n принимает любые положительные целые значения, начиная с 1. С аналогичной ситуацией мы уже встречались при рассмотрении колебаний струны, закрепленной с двух концов (см. Ч. 3, лекция N 6, § 6). С волновым числом k связана энергия частицы E (7.16). Следовательно, квантование волнового числа приводит к квантованию энергии частицы в потенциальной яме:
Подставляя сюда kn из (7.20), получим формулу для стационарных состояний энергии частицы в одномерной бесконечно глубокой потенциальной яме шириной a:
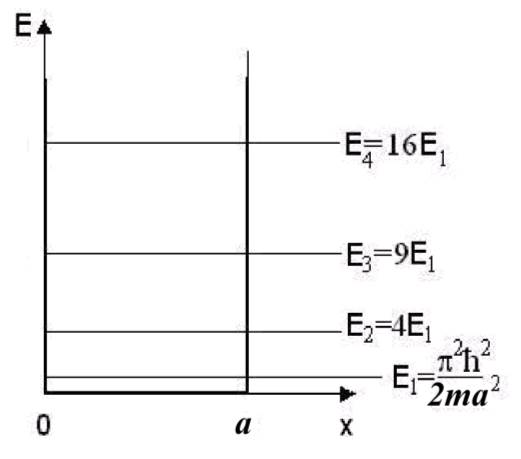
Схема энергетических уровней частицы в яме выглядит следующим образом:
Рис. 7.2 Расстояния между соседними уровнями:
Оценим ΔEn для молекулы (m ~ 10-26 кг), находящейся в сосуде размером a ~ 0,lм.
Расстояния между уровнями в этом случае столь малы, что их дискретность совершенно несущественна. Ситуация меняется, если аналогичную оценку сделать для электрона (me = 9,1?·10-31 кг), локализованного в области порядка атомных размеров (a ~ 10-10 м). В этом случае:
и дискретность уровней будет определять поведение частицы. Условие нормировки (6.5) для нашей волновой функции (7.18) имеет следующий вид:
Интеграл равен a /2, значит
Подставляя константу C в волновую функцию (7.18) и учитывая условия квантования для волнового числа k (7.20), получим нормированные волновые функции для частицы в бесконечно глубокой одномерной потенциальной яме:
Каждая из этих волновых функций задает квантовое состояние частицы с квантовым числом n. В соответствии с вероятностным смыслом волновой функции (6.3) вероятность dwn обнаружить нашу частицу в интервале от x до x + dx, если она находится в квантовом состоянии ψn, дается следующим выражением:
Плотность вероятностиобнаружения частицы:
Графики волновых функций первых двух квантовых состояний и соответствующие графики плотности вероятности приведены на рисунках 7.3а,б.
Рис. 7.3 а,б Из графика плотности вероятности для состояния с n = 2 видно, что точно посередине ямы частица не может быть обнаружена, т.к. там ψ22 = 0. По классическим же представлениям частица должна была двигаться равномерно внутри ямы, отражаясь от ее стенок. Ясно, что при этом все положения частицы в яме равновероятные. Итоги лекции N 7
здесь
U - потенциальная энергия частицы во внешнем поле, которая может зависеть и от времени;
здесь Е - полная энергия частицы в стационарном состоянии, ψ(x,y,z) - координатная волновая функция.
таким образом, |ψ|2 в случае стационарных состояний определяет плотность вероятности обнаружения частицы.
здесь а - размер ямы; m - масса частицы, n - целое число, n = 1,2... Таким образом, уравнение Шредингера предсказывает квантование энергии микрочастицы, движущейся в ограниченной области.
ЛЕКЦИЯ N 8
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.007 с.) |














 - волновое число.
- волновое число.



 не меняется.
не меняется.



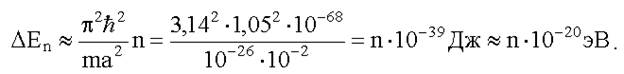







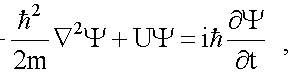
 - оператор Лапласа, в декартовой системе координат он имеет следующий вид:
- оператор Лапласа, в декартовой системе координат он имеет следующий вид: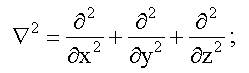
 - мнимая единица.
- мнимая единица.
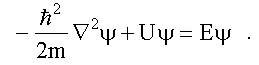

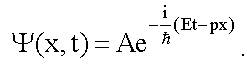
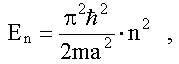
 .
.


