

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Оператор момента импульса частицы
В классической физике момент импульса:

Операторы момента импульса:
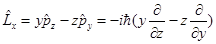


Если результатом действия оператора  на функцию u является та же функция, умноженная на число λ, то число λ называется собственным значением оператора на функцию u является та же функция, умноженная на число λ, то число λ называется собственным значением оператора  , а функция u – собственной функцией , а функция u – собственной функцией  . .

Собственные функции в квантовой теории должны удовлетворять условиям непрерывности, конечности, гладкости, однозначности.
Совокупность собственных значений оператора называется его спектром.
Именно собственные значения обнаруживаются в эксперименте.
14.Основные сведения из теории операторов.
Одна из основных задач квантовой механики состоит в определении вероятности получения того или иного значения динамических переменных, характеризующих частицу или квантовую систему. Причём в квантовой физике не только координаты и скорости, но и другие физические величины не могут иметь определённые значения. Поэтому говорят лишь о вероятности системы иметь то или иное значение величины её характеризующей: энергии, импульса, координаты и т. д. В связи с эти в квантовой физике физическая величина характеризуется её не численным значением, а оператором, который эта физическая величина представляет. Оператором называют правило, по которому любой функции из некоторого пространства сопоставляется другая функция из этого же пространства, то есть 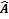 u=v.
· Операторы, используемые в квантовой механике, всегда линейные. Оператор u=v.
· Операторы, используемые в квантовой механике, всегда линейные. Оператор  называется линейным, если для произвольных функций u и v, и произвольных постоянных α и β выполнено равенство: называется линейным, если для произвольных функций u и v, и произвольных постоянных α и β выполнено равенство: 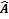 (αu+βv)=α (αu+βv)=α 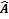 u+β u+β 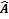 v.
· Операторы Ĉ,Ĉ1, называют суммой, разностью операторов v.
· Операторы Ĉ,Ĉ1, называют суммой, разностью операторов  и и  соответственно, если справедливы равенства: Ĉu= соответственно, если справедливы равенства: Ĉu= 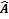 u+ u+  u, Ĉ1u= u, Ĉ1u= 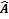 u- u-  u,.
· В общем случае u,.
· В общем случае  . Если выполняется условие . Если выполняется условие  ,то операторы ,то операторы 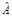 и и  называются коммутирующими, а запись называются коммутирующими, а запись  называется коммутатором операторов называется коммутатором операторов  и и  .
Если .
Если 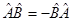 ,то операторы ,то операторы  и и  называются антикоммутирующими, и запись называются антикоммутирующими, и запись  · Если результатом действия оператора
· Если результатом действия оператора 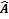 на функцию u является функция u, умноженная на некоторое число λ, то это число называют собственным значением оператора на функцию u является функция u, умноженная на некоторое число λ, то это число называют собственным значением оператора 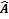 , а функцию u – собственной функцией оператора, соответствующей этому собственному значению: , а функцию u – собственной функцией оператора, соответствующей этому собственному значению: 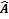 u= λ u. Причём, собственные функции в квантовой механике должны удовлетворять свойствам конечности, непрерывности, однозначности и гладкости. Совокупность собственных значений оператора называется его спектром. Спектр оператора может быть как дискретным, так и непрерывным. Причём, возможны случаи, часть спектра дискретна, а часть непрерывна. Возможны также случаи, когда одному собственному значению соответствует несколько собственных функций. Такое собственное значение называют вырожденным.
· Помимо линейности, на квантово-механические операторы накладывается требование самосопряжённости. Оператор u= λ u. Причём, собственные функции в квантовой механике должны удовлетворять свойствам конечности, непрерывности, однозначности и гладкости. Совокупность собственных значений оператора называется его спектром. Спектр оператора может быть как дискретным, так и непрерывным. Причём, возможны случаи, часть спектра дискретна, а часть непрерывна. Возможны также случаи, когда одному собственному значению соответствует несколько собственных функций. Такое собственное значение называют вырожденным.
· Помимо линейности, на квантово-механические операторы накладывается требование самосопряжённости. Оператор 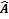 называется самосопряжённым или эрмитовым,если для произвольных функций u и v справедливо равенство: называется самосопряжённым или эрмитовым,если для произвольных функций u и v справедливо равенство:  собственными значениями самосопряжённых операторов являются действительные числа. Собственные значения, как-либо описывающие физическую величину, измеряются в эксперименте. Вообще говоря, физическую величину можно измерить, если её оператор эрмитовый.
Теорема 1. Собственные функции линейного эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть собственными значениями самосопряжённых операторов являются действительные числа. Собственные значения, как-либо описывающие физическую величину, измеряются в эксперименте. Вообще говоря, физическую величину можно измерить, если её оператор эрмитовый.
Теорема 1. Собственные функции линейного эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть
 Док-во: Запишем по определению собственного значения:
Док-во: Запишем по определению собственного значения: 
 . Теперь, подставляя сюда формулы (1), получим: . Теперь, подставляя сюда формулы (1), получим:
 – константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим: – константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим:   Так как собственная функция определяется лишь с точностью до произвольного множителя, то этот множитель можно выбрать так, чтобы функции были ортонормированными:
Так как собственная функция определяется лишь с точностью до произвольного множителя, то этот множитель можно выбрать так, чтобы функции были ортонормированными: 
|
16. Условие одновременной измеримости динамических переменных
Из постулатов квантовой механики следует, что при измерении некоторой физической величины получается определённое значение лишь в том случае, когда волновая функция, описывающая систему, является собственной функцией оператора измеряемой величины. В общем случае различные операторы имеют различные собственные функции, то есть описываемые ими физические величины не могут одновременно иметь точно определённые значения, но в некоторых случаях это возможно. Необходимым и достаточным условием того, чтобы две физические величины имели одновременно определённые значения, является коммутативность операторов, описывающих эти величины. Докажем это утверждение.  Необходимость. Пусть операторы Необходимость. Пусть операторы  имеют общую собственную функцию, а значит описываемые ими физические величины, одновременно имеют определённые значения имеют общую собственную функцию, а значит описываемые ими физические величины, одновременно имеют определённые значения 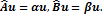 Умножим эти выражения на Умножим эти выражения на  соответств.: соответств.:
 Так как по условию функция
Так как по условию функция  не нулевая, то не нулевая, то  , то есть операторы , то есть операторы  коммутирующие.
Операторы коммутирующие.
Операторы  имеют общую собственную функцию имеют общую собственную функцию  , и поэтому соответствующие им динамические переменные являются одновременно измеримыми с какой угодно степенью точности.
Проверим, являются ли одновременно измеримыми проекция импульса на координату и сама эта координата: , и поэтому соответствующие им динамические переменные являются одновременно измеримыми с какой угодно степенью точности.
Проверим, являются ли одновременно измеримыми проекция импульса на координату и сама эта координата:  . Найдём их коммутатор: . Найдём их коммутатор:
 Подействуем этим оператором на функцию f:
Подействуем этим оператором на функцию f:  То есть оператор коммутатора не равен нулю. Значит операторы
То есть оператор коммутатора не равен нулю. Значит операторы  не коммутирующие. Значит, координата и проекция импульса не могут одновременно иметь определённые значения. Соотношение между дисперсией координаты и импульсом частицы было установлено Гейзенбергом (1927 г.) и получило в последствии название соотношения неопределённостей Гейзенберга. Найдём его. По определению дисперсии мы можем записать не коммутирующие. Значит, координата и проекция импульса не могут одновременно иметь определённые значения. Соотношение между дисперсией координаты и импульсом частицы было установлено Гейзенбергом (1927 г.) и получило в последствии название соотношения неопределённостей Гейзенберга. Найдём его. По определению дисперсии мы можем записать  . Аналогично для импульса: . Аналогично для импульса:
 . Выберем такую систему координат, в которой <x>=0 и <p>=0. В этой системе координат дисперсия координаты и импульса будет . Выберем такую систему координат, в которой <x>=0 и <p>=0. В этой системе координат дисперсия координаты и импульса будет 
 Для нахождения связи между неопределённостью координаты и неопределённостью импульса, Гейзенберг предложил рас/ть ∫ вида:
Для нахождения связи между неопределённостью координаты и неопределённостью импульса, Гейзенберг предложил рас/ть ∫ вида:
 Раскроем теперь скобки и приведём подобные члены. Причём, запишем полученное выражение как многочлен относительно степеней
Раскроем теперь скобки и приведём подобные члены. Причём, запишем полученное выражение как многочлен относительно степеней 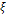 :. :. 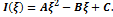 Так как подынтегральное выражение являлось квадратом модуля, то интегральная функция Так как подынтегральное выражение являлось квадратом модуля, то интегральная функция  будет положительно определена: будет положительно определена:  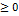 (1). Запишем теперь выражения для коэффициентов (1). Запишем теперь выражения для коэффициентов 
 Беря полученный интеграл по частям, запишем:
Беря полученный интеграл по частям, запишем:
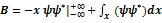 . Первое слагаемое здесь равно нулю, а второе 1 в силу условия нормировки. . Первое слагаемое здесь равно нулю, а второе 1 в силу условия нормировки.
 Запишем теперь условие положительной определённости (1): дискриминант (1) должен быть меньше либо равен нулю:
Запишем теперь условие положительной определённости (1): дискриминант (1) должен быть меньше либо равен нулю:
 Подставляя в последнее выражение значения A,B и С, получим:
Подставляя в последнее выражение значения A,B и С, получим:
 Возвращаясь к определению дисперсии в выбранной нами
Возвращаясь к определению дисперсии в выбранной нами 
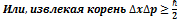 Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения. Под процессом измерения в квантовой физике понимается процесс взаимодействия с любым классическим объектом (прибором). Наличие же наблюдателя вовсе не обязательно. Таким образом, измерения объективны.
Для других сопряженных величин – энергии E и времени tсоотношения неопределенностей,имеет вид: Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения. Под процессом измерения в квантовой физике понимается процесс взаимодействия с любым классическим объектом (прибором). Наличие же наблюдателя вовсе не обязательно. Таким образом, измерения объективны.
Для других сопряженных величин – энергии E и времени tсоотношения неопределенностей,имеет вид:  . Это означает, что при характерном времени эволюции системы Δ t, погрешность определения ее энергии не может быть меньше чем . Это означает, что при характерном времени эволюции системы Δ t, погрешность определения ее энергии не может быть меньше чем  . Из этого соотношения следует возможность возникновения из ничего, так называемых, виртуальных частиц на промежуток времени меньший, чем . Из этого соотношения следует возможность возникновения из ничего, так называемых, виртуальных частиц на промежуток времени меньший, чем  и обладающих энергией Δ E. При этом закон сохранения энергии не будет нарушен. Поэтому по современным представлениям вакуум это не пустота, в которой отсутствуют поля и частицы, а физическая сущность, в которой постоянно возникают и исчезают виртуальные частицы. Одним из
Если в классической физике измерение не возмущало сам объект, то в квантовой механике каждое измерение разрушает объект, уничтожая его волновую функцию. Для нового измерения объект нужно готовить заново. В этой связи Н. Бор выдвинул принцип дополнительности, суть которого в том, что для полного описания объектов микромира необходимо использование, двух противоположных, но дополняющих друг друга представлений. и обладающих энергией Δ E. При этом закон сохранения энергии не будет нарушен. Поэтому по современным представлениям вакуум это не пустота, в которой отсутствуют поля и частицы, а физическая сущность, в которой постоянно возникают и исчезают виртуальные частицы. Одним из
Если в классической физике измерение не возмущало сам объект, то в квантовой механике каждое измерение разрушает объект, уничтожая его волновую функцию. Для нового измерения объект нужно готовить заново. В этой связи Н. Бор выдвинул принцип дополнительности, суть которого в том, что для полного описания объектов микромира необходимо использование, двух противоположных, но дополняющих друг друга представлений.
16. Частица в прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
Потенциальной ямой называется область пространства, в которой потенциальная энергия меньше, чем в окружающем пространстве. В частности движение электрона в кулоновском потенциале ядра есть движение в потенциальной яме. Рассмотрим простейший случай одномерной потенциальной ямы с бесконечно высокими стенками. Её можно описать следующими уравнениями:
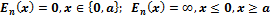 Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы:
Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы:  . Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и. . Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и.  функцию только внутри ямы. Стационарное уравнение
функцию только внутри ямы. Стационарное уравнение  Здесь E – энергия частицы. Запишем граничные условия:
Здесь E – энергия частицы. Запишем граничные условия:

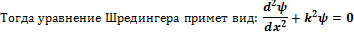 Решением данного уравнения является функция
Решением данного уравнения является функция


 Применим теперь второе граничное условие: Применим теперь второе граничное условие: 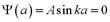 . То есть . То есть 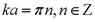 . Получается, что k зависит от n. Тогда . Получается, что k зависит от n. Тогда  . Очевидно, что k принимает дискретные значения. Вспоминая, что . Очевидно, что k принимает дискретные значения. Вспоминая, что  , получим с учётом последнего выражения: , получим с учётом последнего выражения:  . Отсюда . Отсюда 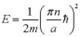 , причём минимальная энергия равна: , причём минимальная энергия равна: 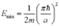 . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид: . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид:  . Волновая функция основного состояния . Волновая функция основного состояния  . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу A из условия нормировки: вероятность нахождения частицы внутри ямы равна 1: . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу A из условия нормировки: вероятность нахождения частицы внутри ямы равна 1:  . .  . Отсюда . Отсюда  и для волновой функции имеем: и для волновой функции имеем: 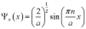 . .
|
|
|




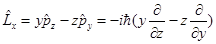


 на функцию u является та же функция, умноженная на число λ, то число λ называется собственным значением оператора
на функцию u является та же функция, умноженная на число λ, то число λ называется собственным значением оператора 
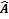 u=v.
· Операторы, используемые в квантовой механике, всегда линейные. Оператор
u=v.
· Операторы, используемые в квантовой механике, всегда линейные. Оператор  называется линейным, если для произвольных функций u и v, и произвольных постоянных α и β выполнено равенство:
называется линейным, если для произвольных функций u и v, и произвольных постоянных α и β выполнено равенство:  соответственно, если справедливы равенства: Ĉu=
соответственно, если справедливы равенства: Ĉu=  . Если выполняется условие
. Если выполняется условие  ,то операторы
,то операторы 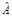 и
и  называются коммутирующими, а запись
называются коммутирующими, а запись  называется коммутатором операторов
называется коммутатором операторов 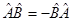 ,то операторы
,то операторы  · Если результатом действия оператора
· Если результатом действия оператора  собственными значениями самосопряжённых операторов являются действительные числа. Собственные значения, как-либо описывающие физическую величину, измеряются в эксперименте. Вообще говоря, физическую величину можно измерить, если её оператор эрмитовый.
Теорема 1. Собственные функции линейного эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть
собственными значениями самосопряжённых операторов являются действительные числа. Собственные значения, как-либо описывающие физическую величину, измеряются в эксперименте. Вообще говоря, физическую величину можно измерить, если её оператор эрмитовый.
Теорема 1. Собственные функции линейного эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть
 Док-во: Запишем по определению собственного значения:
Док-во: Запишем по определению собственного значения: 
 . Теперь, подставляя сюда формулы (1), получим:
. Теперь, подставляя сюда формулы (1), получим:
 – константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим:
– константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим: 
 Так как собственная функция определяется лишь с точностью до произвольного множителя, то этот множитель можно выбрать так, чтобы функции были ортонормированными:
Так как собственная функция определяется лишь с точностью до произвольного множителя, то этот множитель можно выбрать так, чтобы функции были ортонормированными: 
 Необходимость. Пусть операторы
Необходимость. Пусть операторы  имеют общую собственную функцию, а значит описываемые ими физические величины, одновременно имеют определённые значения
имеют общую собственную функцию, а значит описываемые ими физические величины, одновременно имеют определённые значения 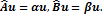 Умножим эти выражения на
Умножим эти выражения на  Так как по условию функция
Так как по условию функция  не нулевая, то
не нулевая, то  , то есть операторы
, то есть операторы  коммутирующие.
Операторы
коммутирующие.
Операторы  , и поэтому соответствующие им динамические переменные являются одновременно измеримыми с какой угодно степенью точности.
Проверим, являются ли одновременно измеримыми проекция импульса на координату и сама эта координата:
, и поэтому соответствующие им динамические переменные являются одновременно измеримыми с какой угодно степенью точности.
Проверим, являются ли одновременно измеримыми проекция импульса на координату и сама эта координата:  . Найдём их коммутатор:
. Найдём их коммутатор:
 Подействуем этим оператором на функцию f:
Подействуем этим оператором на функцию f:  То есть оператор коммутатора не равен нулю. Значит операторы
То есть оператор коммутатора не равен нулю. Значит операторы  . Аналогично для импульса:
. Аналогично для импульса:
 . Выберем такую систему координат, в которой <x>=0 и <p>=0. В этой системе координат дисперсия координаты и импульса будет
. Выберем такую систему координат, в которой <x>=0 и <p>=0. В этой системе координат дисперсия координаты и импульса будет 
 Для нахождения связи между неопределённостью координаты и неопределённостью импульса, Гейзенберг предложил рас/ть ∫ вида:
Для нахождения связи между неопределённостью координаты и неопределённостью импульса, Гейзенберг предложил рас/ть ∫ вида:
 Раскроем теперь скобки и приведём подобные члены. Причём, запишем полученное выражение как многочлен относительно степеней
Раскроем теперь скобки и приведём подобные члены. Причём, запишем полученное выражение как многочлен относительно степеней 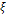 :.
:. 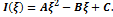 Так как подынтегральное выражение являлось квадратом модуля, то интегральная функция
Так как подынтегральное выражение являлось квадратом модуля, то интегральная функция  будет положительно определена:
будет положительно определена: 
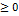 (1). Запишем теперь выражения для коэффициентов
(1). Запишем теперь выражения для коэффициентов 
 Беря полученный интеграл по частям, запишем:
Беря полученный интеграл по частям, запишем:
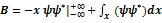 . Первое слагаемое здесь равно нулю, а второе 1 в силу условия нормировки.
. Первое слагаемое здесь равно нулю, а второе 1 в силу условия нормировки.
 Запишем теперь условие положительной определённости (1): дискриминант (1) должен быть меньше либо равен нулю:
Запишем теперь условие положительной определённости (1): дискриминант (1) должен быть меньше либо равен нулю:
 Подставляя в последнее выражение значения A,B и С, получим:
Подставляя в последнее выражение значения A,B и С, получим:
 Возвращаясь к определению дисперсии в выбранной нами
Возвращаясь к определению дисперсии в выбранной нами 
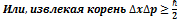 Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения. Под процессом измерения в квантовой физике понимается процесс взаимодействия с любым классическим объектом (прибором). Наличие же наблюдателя вовсе не обязательно. Таким образом, измерения объективны.
Для других сопряженных величин – энергии E и времени tсоотношения неопределенностей,имеет вид:
Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения. Под процессом измерения в квантовой физике понимается процесс взаимодействия с любым классическим объектом (прибором). Наличие же наблюдателя вовсе не обязательно. Таким образом, измерения объективны.
Для других сопряженных величин – энергии E и времени tсоотношения неопределенностей,имеет вид:  . Это означает, что при характерном времени эволюции системы Δ t, погрешность определения ее энергии не может быть меньше чем
. Это означает, что при характерном времени эволюции системы Δ t, погрешность определения ее энергии не может быть меньше чем  . Из этого соотношения следует возможность возникновения из ничего, так называемых, виртуальных частиц на промежуток времени меньший, чем
. Из этого соотношения следует возможность возникновения из ничего, так называемых, виртуальных частиц на промежуток времени меньший, чем  и обладающих энергией Δ E. При этом закон сохранения энергии не будет нарушен. Поэтому по современным представлениям вакуум это не пустота, в которой отсутствуют поля и частицы, а физическая сущность, в которой постоянно возникают и исчезают виртуальные частицы. Одним из
Если в классической физике измерение не возмущало сам объект, то в квантовой механике каждое измерение разрушает объект, уничтожая его волновую функцию. Для нового измерения объект нужно готовить заново. В этой связи Н. Бор выдвинул принцип дополнительности, суть которого в том, что для полного описания объектов микромира необходимо использование, двух противоположных, но дополняющих друг друга представлений.
и обладающих энергией Δ E. При этом закон сохранения энергии не будет нарушен. Поэтому по современным представлениям вакуум это не пустота, в которой отсутствуют поля и частицы, а физическая сущность, в которой постоянно возникают и исчезают виртуальные частицы. Одним из
Если в классической физике измерение не возмущало сам объект, то в квантовой механике каждое измерение разрушает объект, уничтожая его волновую функцию. Для нового измерения объект нужно готовить заново. В этой связи Н. Бор выдвинул принцип дополнительности, суть которого в том, что для полного описания объектов микромира необходимо использование, двух противоположных, но дополняющих друг друга представлений.
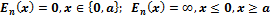 Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы:
Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы:  . Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и.
. Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и.  функцию только внутри ямы. Стационарное уравнение
функцию только внутри ямы. Стационарное уравнение  Здесь E – энергия частицы. Запишем граничные условия:
Здесь E – энергия частицы. Запишем граничные условия:

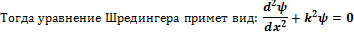 Решением данного уравнения является функция
Решением данного уравнения является функция


 Применим теперь второе граничное условие:
Применим теперь второе граничное условие: 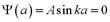 . То есть
. То есть 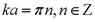 . Получается, что k зависит от n. Тогда
. Получается, что k зависит от n. Тогда  . Очевидно, что k принимает дискретные значения. Вспоминая, что
. Очевидно, что k принимает дискретные значения. Вспоминая, что  , получим с учётом последнего выражения:
, получим с учётом последнего выражения:  . Отсюда
. Отсюда 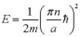 , причём минимальная энергия равна:
, причём минимальная энергия равна: 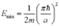 . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид:
. Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид:  . Волновая функция основного состояния
. Волновая функция основного состояния  . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу A из условия нормировки: вероятность нахождения частицы внутри ямы равна 1:
. Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу A из условия нормировки: вероятность нахождения частицы внутри ямы равна 1:  .
.  . Отсюда
. Отсюда  и для волновой функции имеем:
и для волновой функции имеем: 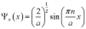 .
.



