

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Опыты Резерфорда Ядерная модель атома.
Постулаты квантовой механики.
Квантовая теория базируется на нескольких основных положениях, принимаемых без доказательств:
1) Состояние движения квантового объекта описывается волновой функцией  . .
Для электромагнитной волны: 
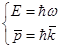 => => 
Тогда 
2) Волновая функция подчиняется уравнению Шредингера
 , где , где  - оператор полной энергии системы (Гамильтона) - оператор полной энергии системы (Гамильтона)


3) Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.
4) При измерении некоторой динамической переменной, описываемой оператором  , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность получения при измерении собственного значения , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность получения при измерении собственного значения  равна равна  , где , где 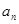 - коэффициенты разложения волновой функции - коэффициенты разложения волновой функции  по собственным функциям оператора по собственным функциям оператора  . .



Среднее значение динамической переменной можно найти с помощью волновой функции Ψ.

Согласно третьему постулату операторы, описывающие переменные, должны быть линейными и эрмитовыми.
Оператор координаты является оператором умножения на эту координату:  . Например . Например 
Оператор проекции импульса?
Оператор проекции импульса на оси декартовой системы координат:
 ; ;  ; ; 
Например 
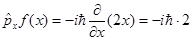
Оператор полного импульса
Оператор полного импульса 
Оператор Гамильтона
Оператор Гамильтона может быть получен как оператор импульса. В классической физике функцией Гамильтона называется полная энергия системы, выраженная через обобщение координаты и обобщение импульса:
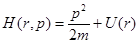 , где U(r) – потенциальная энергия , где U(r) – потенциальная энергия
Оператор Гамильтона:

Одномерная яма конечной глубины.

Предполагается (рис. 56), что при х < 0 потенциальная энергия обращается в бесконечность. Значит, частица не может проникнуть в область х < 0 и, следовательно, в этой области волновая функция равна нулю. Поэтому достаточно найти волновую функцию в областях lull при х > 0, заметив, что в точке х = 0 из-за непрерывности волновая функция обращается в нуль.
Уравнение Шредингера в областях I (0 < х < а) и II (а < х <∞) имеет вид
(I) 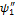 + +   = 0, = 0,  =2тЕ/ћ2, =2тЕ/ћ2,
(II)  + (2т/ћ2)(Е - Еп0) + (2т/ћ2)(Е - Еп0)  = 0. (26.10) = 0. (26.10)
Случай Е > Еп0. Уравнение Шредингера в области II
(II)  + +   = 0, = 0,  =(2т/ћ2)(Е - Еп0) > 0,(26.11) =(2т/ћ2)(Е - Еп0) > 0,(26.11)
а в области I оно имеет вид (26.10; I). Решения для различных областей можно записать следующим образом:
(I)  = Al sin(k1x) + Bl cos(k1x),(26.12) = Al sin(k1x) + Bl cos(k1x),(26.12)
(II)  = A2sin[k2(x-a)] + В 2cos[k2(x-a)]. = A2sin[k2(x-a)] + В 2cos[k2(x-a)].
Из условия  (0) = 0 следует, что В1 = 0, а условия непрерывности функции и ее производной (0) = 0 следует, что В1 = 0, а условия непрерывности функции и ее производной
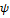 1(a) = 1(a) = 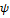 2(a), 2(a),  (a) = (a) =  (a) (26.13) (a) (26.13)
дают для коэффициентов А2 и В2 следующие выражения:
А2 = (k1A1/k2)cos(k1a), В2 = А1 sin(k1a).(26.14)
Эти условия могут быть всегда удовлетворены. Поэтому в случае Е > Еи0 спектр энергии непрерывен, частица при своем движении не локализована в конечной области пространства, ее движение инфинитно.
Случай Е < Еп0. Уравнение Шредингера в области II имеет вид (II)  +k2 +k2  = 0 к2= (2 т/ћ2)(Еп0 - Е) > 0. (26.15) = 0 к2= (2 т/ћ2)(Еп0 - Е) > 0. (26.15)
В области I уравнение остается без изменения. Решения для областей I и II представляются функциями
(I)  = А 1sin (k1x),(26.16) = А 1sin (k1x),(26.16)
(II)  = С2е-кх + D2ekx. = С2е-кх + D2ekx.
Так как волновая функция везде должна быть конечной, а екх при х->∞ неограниченно возрастает, то D2 в формуле (26.16; II) необходимо принять равным нулю.
Условия сшивания (26.13) в рассматриваемом случае:
А1 sin(k1a) = С2ехр(- ка), (26.17)
Alk1cos(k2a) = -кС2ехр(-ка).
Разделив почленно второе уравнение на первое, получим условие квантования энергии:
k1ctg(k1a) = -к. (26.18)
Для графического решения этого уравнения удобно сделать следующие преобразования:
sin (k1a) = [1 + ctg2k1a)]-1/2 = [1+(k/k1)2] -1/2 =[1+(Еп0-E)/E]-1/2 = (Е/Еп0)1/2.
Но  = ћk1/ = ћk1/ 
и, следовательно, уравнение (26.18) принимает вид
sin у = (ћ/  )у (y=k1a)• (26.19) )у (y=k1a)• (26.19)
Это уравнение решается с помощью построения, указанного на рис. 57. В качестве решений берутся не все пер есечения прямой z = (ћy/ 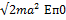 ) с синусоидой z = siny, а лишь те, которые согласуются со знаком в уравнении (26.18), т. е. точки пересечения в четных четвертях. Этим значениям уп, которых имеется конечное число, соответствуют энергии ) с синусоидой z = siny, а лишь те, которые согласуются со знаком в уравнении (26.18), т. е. точки пересечения в четных четвертях. Этим значениям уп, которых имеется конечное число, соответствуют энергии
Еn = ћ2y2/ 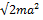 (26.20) (26.20)
Таким образом, в потенциальной яме с конечной глубиной имеется конечное число собственных значений энергии.
Волновая функция при х > а, согласно (26.16; II), имеет вид
 = С2е-кх (26.21) = С2е-кх (26.21)
Эффект Зеемана.
Как известно, полный механический момент атома  . Тогда проекция . Тогда проекция  на какое-либо направление, в силу пространственного квантования, будет принимать на какое-либо направление, в силу пространственного квантования, будет принимать 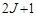 значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать 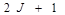 значение. Каждой ориентации магнитного момента значение. Каждой ориентации магнитного момента  будет соответствовать своя энергия взаимодействия атома с магнитным полем: будет соответствовать своя энергия взаимодействия атома с магнитным полем:  . В этом случае . В этом случае  . Значит, возможны . Значит, возможны  энергии взаимодействия. Таким образом, и полная энергия атома принимает энергии взаимодействия. Таким образом, и полная энергия атома принимает  значение, то есть уровень энергии расщепляется на значение, то есть уровень энергии расщепляется на  компоненту, а величина расщепления определяется значениями проекции магнитного момента или механического момента. Для нахождения возможных линий излучения необходимо учесть следующие правила отбора для излучательных переходов: компоненту, а величина расщепления определяется значениями проекции магнитного момента или механического момента. Для нахождения возможных линий излучения необходимо учесть следующие правила отбора для излучательных переходов:
 ; ;  ; ;  ; ; 
Каждый из возможных переходов приводит к излучению отдельной линии. Явление расщепления спектральных линий при помещении атома в слабое внешнее магнитное поле называют аномальным (сложным) эффектом Зеемана. Полная энергия равна, как было записано выше:  . Энергия излучения, при переходе с одного уровня на другой, равна: . Энергия излучения, при переходе с одного уровня на другой, равна:  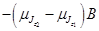 . Таким образом, изменение частоты . Таким образом, изменение частоты  будет равно: будет равно:   , ,  . .  называют величину зеемановского расщепления. Так как взаимодействие магнитного момента с внешним магнитным полем меньше, чем спин-орбитальное взаимодействие, то и величина зеемановского расщепления мала. Частота излучения в случае слабого магнитного поля определяется по формуле: называют величину зеемановского расщепления. Так как взаимодействие магнитного момента с внешним магнитным полем меньше, чем спин-орбитальное взаимодействие, то и величина зеемановского расщепления мала. Частота излучения в случае слабого магнитного поля определяется по формуле:  . .
Определим величину смещения частоты при эффекте Зеемана  : : 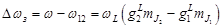 . .
Если величина зеемановского расщепления равна частоте ланморовой прецессии,  , то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда , то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда  . Для первого уровня . Для первого уровня  , а , а  . Таким образом, так как . Таким образом, так как  , а , а 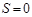 , то , то  . Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление: . Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление:
 . .
Такой эффект называют простым (нормальным) эффектом Зеемана. Так как поле слабое, расщепление Зеемана будет меньше естественного (мультиплетного) расщепления, вызванного спин-орбитальным взаимодействием.
29. Эффект Пашена – Бака.
Рассмотрим теперь случай, когда индукция магнитного поля велика. В данной ситуации энергия взаимодействия магнитного момента атома с полем становится больше спин-орбитального взаимодействия и связь между спиновыми и орбитальными моментами разрушается. Каждый в отдельности начинает взаимодействовать с полем. Это явление разрыва спин-орбитальной связи в магнитном поле называется эффектом Пашена – Бака. Энергия уровня, в данном случае, равна:  , где E0 – начальная энергия уровня до помещения его в магнитное поле. , где E0 – начальная энергия уровня до помещения его в магнитное поле. 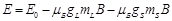 – запись через проекции – запись через проекции  на на  . Тогда . Тогда  . Казалось бы, спектр должен быть очень богатым, ведь возможны . Казалось бы, спектр должен быть очень богатым, ведь возможны  проекция проекция  и ещё две проекции и ещё две проекции 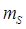 . Найдём его. . Найдём его.  . Для одного уровня . Для одного уровня 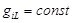 , ,  : :  , ,  . .  ; ;  . Тогда, если . Тогда, если  и и  , ,  . Следовательно, . Следовательно,  . Таким образом, может расщепляться на три компоненты: . Таким образом, может расщепляться на три компоненты:  ; ;  . В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три. . В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три.
Рентгеновские спектры.
Рентгеновские спектры бывают двух видов: сплошные и линейчатые. Сплошные спектры возникают при торможении быстрых эл-нов в вещ-ве антикатода и являются обычным тормозным излучением эл-нов. Линейчатый спектр состоит из отдельных линий излучения. Он зависит от материала антикатода и полностью характеризуется им. Каждый эл-т обладает характерным для него линейчатым спектром. Между рентгеновскими линейными спектрами и оптическими линецчатыми спектрами существует три различия. Во-первых, частота рентгеновского излучения во много раз больше оптического. Значит энергия рентгеновского кванта в тысячи раз больше энергии оптического кванта. Во-вторых, рентгеноспектры различных эл-тов имеют одинаковую структуру, тогда так структура оптических спектров различных эл-тов существенно различается. В-третьих оптические спектры поглощения состоят из отдельных линий, совпадающих с линиями излучения главной серии соответств эл-та. Рентгеновские спектры поглощения не похожи на рентгеновские спектры испускания: они состоят из нескольких полос с резким длинноволновым краем. Объяснение: эл-н, падающий на материал антикатода, сталкиваясь с атомами антикатодо, может выбить эл-н с одной из внутренних оболочек атома. Эл-ны более внешних оболочек могут переходить на свободное место. В результате оспускается квант рентгеновского излучения. Энергия эл-на в кулоновском поле ядра:

Энергия эл-на на одной из внутренних оболочек:

При переходе эл-на на освободившееся место на внутренней оболочке с внешней оболочки излучается квант с частотой:

Опыты Резерфорда Ядерная модель атома.
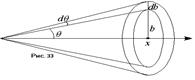
  Модель Резерфорда, приписывала атому строение, аналогичное строению Солнечной системы: в центре находится положительно заряженное ядро, вокруг которого, подобно планетам, движутся электроны, удерживаемые у ядра силами кулоновского притяжения.. Резерфорд изучал движение тяжёлых положительно заряженных частиц в поле, создаваемом атомом.. Узкий пучок Модель Резерфорда, приписывала атому строение, аналогичное строению Солнечной системы: в центре находится положительно заряженное ядро, вокруг которого, подобно планетам, движутся электроны, удерживаемые у ядра силами кулоновского притяжения.. Резерфорд изучал движение тяжёлых положительно заряженных частиц в поле, создаваемом атомом.. Узкий пучок  – частиц из источника излучения падала на тонкую золотую фольгу. За фольгой находилась поверхность, покрытая веществом, способным сцинтиллировать, например, – частиц из источника излучения падала на тонкую золотую фольгу. За фольгой находилась поверхность, покрытая веществом, способным сцинтиллировать, например,  . .  – частицы пролетали сквозь фольгу и падали на сцинтиллятор. Сцинтиллятор на короткое время начинал светиться в точке падения – частицы пролетали сквозь фольгу и падали на сцинтиллятор. Сцинтиллятор на короткое время начинал светиться в точке падения  – частиц. За этими вспышками как раз и наблюдали. Если бы взаимодействия частиц с веществом не было, то вспышки наблюдались бы все в одном и том же месте. Тем не менее, большинство частиц отклонялись от направления своего первоначального движения на 3°-5°, и что ещё более интересно, приблизительно одна из 6000 – 8000 частиц отклонялась от первоначального направления движения на угол более 90°. В то же время не было частиц, которые притягивались бы - в атоме должен находиться мощный силовой центр, который заставляет отклоняться частицы на большие углы, причём, так как заряд – частиц. За этими вспышками как раз и наблюдали. Если бы взаимодействия частиц с веществом не было, то вспышки наблюдались бы все в одном и том же месте. Тем не менее, большинство частиц отклонялись от направления своего первоначального движения на 3°-5°, и что ещё более интересно, приблизительно одна из 6000 – 8000 частиц отклонялась от первоначального направления движения на угол более 90°. В то же время не было частиц, которые притягивались бы - в атоме должен находиться мощный силовой центр, который заставляет отклоняться частицы на большие углы, причём, так как заряд  – частицы считался положительным, этот силовой центр также должен быть положительным. Редкость отскакивания частицы на угол более 90° говорила о том, что центр должен быть точечным. В центре атома существует нечто, обладающее большой массой и имеющее малые размеры и положительный заряд. Изучая движение частиц сквозь фольгу, Резерфорд получил соотношение, связывающее угол рассеяния частицы с прицельным параметром – частицы считался положительным, этот силовой центр также должен быть положительным. Редкость отскакивания частицы на угол более 90° говорила о том, что центр должен быть точечным. В центре атома существует нечто, обладающее большой массой и имеющее малые размеры и положительный заряд. Изучая движение частиц сквозь фольгу, Резерфорд получил соотношение, связывающее угол рассеяния частицы с прицельным параметром  . Прицельным параметром . Прицельным параметром  называется расстояние наименьшего сближения частиц, при отсутствии взаимодействия между ними (см. рис. 32) называется расстояние наименьшего сближения частиц, при отсутствии взаимодействия между ними (см. рис. 32)
 (4). (4).
  Последняя формула была получена Резерфордом и связывает угол рассеяния частицы с прицельным параметром Последняя формула была получена Резерфордом и связывает угол рассеяния частицы с прицельным параметром  . Оставалось только проверить эту формулу. В опыте Резерфорд имел дело не с одной частицей, а с большим их числом. Частицы двигались под некоторыми углами, то есть имел место некоторый разброс углов. Частицы рассеивались на различных атомах и после рассеяния приобретали некоторые импульсы, значения которых также претерпевали некоторый разброс. Для того чтобы описать данный процесс, немыслимо пытаться рассчитывать траекторию движения каждой частицы. Полученная система уравнений будет слишком громоздка и практически неразрешима. В данном случае уместно прибегнуть к теории вероятностей. Введём понятие дифференциального поперечного сечения рассеяния . Оставалось только проверить эту формулу. В опыте Резерфорд имел дело не с одной частицей, а с большим их числом. Частицы двигались под некоторыми углами, то есть имел место некоторый разброс углов. Частицы рассеивались на различных атомах и после рассеяния приобретали некоторые импульсы, значения которых также претерпевали некоторый разброс. Для того чтобы описать данный процесс, немыслимо пытаться рассчитывать траекторию движения каждой частицы. Полученная система уравнений будет слишком громоздка и практически неразрешима. В данном случае уместно прибегнуть к теории вероятностей. Введём понятие дифференциального поперечного сечения рассеяния  в угол между в угол между  и и  . Так будем называть отношение числа частиц dN . Так будем называть отношение числа частиц dN  , рассеянных в единицу времени в угол , рассеянных в единицу времени в угол  к полному потоку частиц к полному потоку частиц  : :  . Здесь . Здесь  , где , где  – полное число частиц. Все частицы, для которых – полное число частиц. Все частицы, для которых  , будут рассеиваться в угол , будут рассеиваться в угол 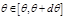 . Число частиц, прицельный параметр которых заключён в этом интервале, будет равно числу частиц, падающих на кольцо шириной db и радиусом внутренней окружности . Число частиц, прицельный параметр которых заключён в этом интервале, будет равно числу частиц, падающих на кольцо шириной db и радиусом внутренней окружности  : :  . Тогда . Тогда  ,. Нам не важен здесь знак db, поэтому в дальнейшем будем рассматривать лишь его модуль. Воспользуемся теперь полученной нами формулой (4) для нахождения | db |: ,. Нам не важен здесь знак db, поэтому в дальнейшем будем рассматривать лишь его модуль. Воспользуемся теперь полученной нами формулой (4) для нахождения | db |:  . .
Подставляя полученное выражение в уравнение для  ,получим, -> ,получим, ->
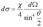 <- Последняя формула называется формулой Резерфорда. Перейдём теперь от плоского угла <- Последняя формула называется формулой Резерфорда. Перейдём теперь от плоского угла  к телесному к телесному  . Известно, что они связаны соотношением . Известно, что они связаны соотношением  в сферической системе координат. Тогда если угол в сферической системе координат. Тогда если угол 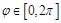 , ,  . Из последней формулы выразим . Из последней формулы выразим  и подставим его в формулу Резерфорда для плоского угла: и подставим его в формулу Резерфорда для плоского угла:  , ,  ; ;  , или , или
<- (5). Мы получили формулу Резерфорда для телесного угла. Данная формула подтверждается с хорошей точностью и при современных исследованиях. Таким образом, косвенно подтвердилось уравнение (4), которое было выведено исходя
из соображений планетарного строения атома, что и утвердило главенствующее положение этой теории. Если известно сечение рассеяния  , то с помощью формул (4) и (5) можно вычислить зарядовое число Z. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа. , то с помощью формул (4) и (5) можно вычислить зарядовое число Z. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа.

10.Постулаты Бора, правила квантования. Структура спектральных термов атома водорода.
При всём удобстве планетарной модели атом по Резерфорду, очевидна её неустойчивость. Действительно, электроны движутся по орбитам с центростремительным ускорением. Тогда в соответствии с электродинамикой Максвелла, они должны непрерывно излучать. Но тогда они теряли бы энергию и, в конце концов, упали бы на ядро. Расчёты показали, что такой процесс «схлопывания» атома произошёл бы очень быстро. Чтобы разрешить возникшее противоречие, Нильс Бор выдвинул следующие требования к атомной излучающей системе, которые впоследствии назвали постулатами Бора.
1. Атомы могут определённое время, в зависимости от их структурных особенностей, находиться в определённых, так называемых стационарных состояниях. Энергии этих состояний 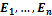 образуют дискретный ряд. В стационарных состояниях атомы не излучают.
2. При переходе атома из одного состояния с энергией образуют дискретный ряд. В стационарных состояниях атомы не излучают.
2. При переходе атома из одного состояния с энергией  в другое с энергией в другое с энергией  , происходит излучение, если , происходит излучение, если  , или поглощение, если , или поглощение, если  кванта света с частотой пропорциональной разности энергий состояний: кванта света с частотой пропорциональной разности энергий состояний:  .
Бор ввёл также правила, в соответствии с которыми определяются стационарные состояния атомных систем. Данные правила получили название правил квантования. Бор предположил, что стационарными являются лишь те состояния, в которых момент импульса электрона равен целому числу постоянных Планка: .
Бор ввёл также правила, в соответствии с которыми определяются стационарные состояния атомных систем. Данные правила получили название правил квантования. Бор предположил, что стационарными являются лишь те состояния, в которых момент импульса электрона равен целому числу постоянных Планка:  . Коэффициент пропорциональности между моментом импульса электрона и постоянной Планка называют главным квантовым числом.
Р-им водородоподобный атом, который представляет собой систему из ядра и одного электрона. Масса ядра много больше массы электрона, поэтому ядро можно считать неподвижным. Для простоты положим, что электрон движется вокруг ядра с зарядом Z по круговой орбите радиусаr. Со стороны ядра на электрон действует кулоновская сила притяжения, сообщая ему центростремительное ускорение . Коэффициент пропорциональности между моментом импульса электрона и постоянной Планка называют главным квантовым числом.
Р-им водородоподобный атом, который представляет собой систему из ядра и одного электрона. Масса ядра много больше массы электрона, поэтому ядро можно считать неподвижным. Для простоты положим, что электрон движется вокруг ядра с зарядом Z по круговой орбите радиусаr. Со стороны ядра на электрон действует кулоновская сила притяжения, сообщая ему центростремительное ускорение
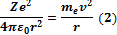 Потенциальная энергия электрона в поле ядра
Потенциальная энергия электрона в поле ядра
 А его полная энергия:
А его полная энергия:
 Момент импульса электрона, вращающегося на n-й орбите, равен:
Момент импульса электрона, вращающегося на n-й орбите, равен:
 Исключая из (2) и (6)
Исключая из (2) и (6)  ,получим для радиуса n-й орбиты ,получим для радиуса n-й орбиты
 Радиус первой боровской орбиты в атоме водорода (n=1, Z=1) равен
Радиус первой боровской орбиты в атоме водорода (n=1, Z=1) равен
 И называется первым боровским радиусом.
Из выр-ий (4) и (7) сразу получается значение энергии электрона, находящегося на n-й орбите:
И называется первым боровским радиусом.
Из выр-ий (4) и (7) сразу получается значение энергии электрона, находящегося на n-й орбите:
 Из (1) и (9), можно получить частоты спектральных линий, возникающих при переходе электрона с одной орбиты на другую:
Из (1) и (9), можно получить частоты спектральных линий, возникающих при переходе электрона с одной орбиты на другую:
 Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины
Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины 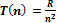 называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов. называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов.
 Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
Общая формула Бальмера для частот спектральных линий:
Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
Общая формула Бальмера для частот спектральных линий:
 Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины
Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины 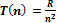 называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов. называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов.
 Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
В спектре испускания водорода наблюдается несколько серий, расположенных в различных областях спектра:
-серия Лаймана (
Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
В спектре испускания водорода наблюдается несколько серий, расположенных в различных областях спектра:
-серия Лаймана ( –ультрафиолетовая область;
-серия Бальмера ( –ультрафиолетовая область;
-серия Бальмера ( –видимая область;
-серия Пашена ( –видимая область;
-серия Пашена ( –инфракрасная область;
-серия Брэкета ( –инфракрасная область;
-серия Брэкета ( –инфракрасная область;
-серия Пфунда ( –инфракрасная область;
-серия Пфунда ( –инфракрасная область; –инфракрасная область;
|
11. Спектральн. линии. Изотопический сдвиг спектр. линий.
Все спектры (испускания, поглощения) делятся на линейчатые, полосатые и сплошные. Чем проще структура вещества, тем разрежённей его спектр. С другой стороны, чем меньше электронов содержит вещество, тем проще его спектр. Линейчатые спектры характерны для атомов определённых веществ. Полосатые спектры дают молекулы газа в разряженном состоянии. Сплошным спектром обладает газ при высокой температуре или жидкость, а также твёрдые тела.
Проведя исследования было обнаружено: что спектральные линии объединяются в серии. Серией называется группа спектральных линий, соответствующая переходу атома с одного и того же энергетического уровня на какой-либо другой (для спектра испускания) либо в одно и то же энергетическое состояние (для спектра поглощения). Первая спектральная серия для атома водорода была обнаружена Бальмером и получила его имя. Изучая спектр атома водорода в видимой  где m=1, 2, 3…. Впоследствии были открыты и остальные серии для атома водорода: где m=1, 2, 3…. Впоследствии были открыты и остальные серии для атома водорода:
 

 Расстояния между спектральными линиями с увеличением числа m становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий:
Расстояния между спектральными линиями с увеличением числа m становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий:
 Причём n определяет номер спектральной серии.
Причём n определяет номер спектральной серии.  для спектра испускания; для спектра испускания; 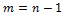 для спектра поглощения. Введём для спектра поглощения. Введём  Таким образом, частота любой спектральной линии определяется
Таким образом, частота любой спектральной линии определяется  Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой: Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой:
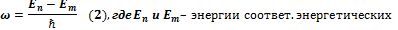 уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае
уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае  В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.
Изотопами наз. элементы, заряд ядра к-ых одинаков, а массы различны. Химические св-ва изотопов весьма близки др. к др.
Дейтрон – ядро атома дейтерия, состоит из протона и нейтрона. Тритон – ядро атома трития, состоит из протона и 2-х нейтронов. Различие в массах ядер различных изотопов приводит к сдвигу линий др. относительно др. в их спектрах излучения – изотопический сдвиг. Он не велик. Например для
В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.
Изотопами наз. элементы, заряд ядра к-ых одинаков, а массы различны. Химические св-ва изотопов весьма близки др. к др.
Дейтрон – ядро атома дейтерия, состоит из протона и нейтрона. Тритон – ядро атома трития, состоит из протона и 2-х нейтронов. Различие в массах ядер различных изотопов приводит к сдвигу линий др. относительно др. в их спектрах излучения – изотопический сдвиг. Он не велик. Например для
 По сдвигу этих линий можно определить массу изотопа, по интенсивности – концентрацию изотопа.
По сдвигу этих линий можно определить массу изотопа, по интенсивности – концентрацию изотопа.
12. Ур-ие Шрёдингера как основа квантово-механического описания дискретных состояний атомов. Собственные значения и собственные ф-ии этого ур-ия, их свойства.
Из основных ур-ий электромагнитного поля вытекает волновое ур-ие для электромагнитных волн. Записываем и подставляем в него решение в виде плоских волн получим соотношение между частотой и составляющими волнового вектора (закон дисперсии):
 Из соотношений между импульсом и энергией ньютоновской
Из соотношений между импульсом и энергией ньютоновской  Воспользуемся квантовыми соотношениями для энергии и составляющих импульса:
Воспользуемся квантовыми соотношениями для энергии и составляющих импульса:
 Подставляя их в (1), сокращая на
Подставляя их в (1), сокращая на  получим: получим:
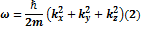 - закон дисперсии волн де Бройля в нерелятивистском приближении. Далее возьмем формулу плоской волны де Бройля и продифференцировав ее 1 раз во времени и 2 по всеми координатам получим:
- закон дисперсии волн де Бройля в нерелятивистском приближении. Далее возьмем формулу плоской волны де Бройля и продифференцировав ее 1 раз во времени и 2 по всеми координатам получим:
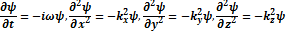 Найдя отсюда
Найдя отсюда  и подставив в закон дисперсии (2): и подставив в закон дисперсии (2):

 Для стоячих монохроматических волн решение может быть представлено в виде произведения 2-х ф-ий, одна из к-ых ф-ия координат, другая - ф-ия времени, зависимость от времени
Для стоячих монохроматических волн решение может быть представлено в виде произведения 2-х ф-ий, одна из к-ых ф-ия координат, другая - ф-ия времени, зависимость от времени  .Для таких решений левая часть (3) дает: .Для таких решений левая часть (3) дает:

 Частицы. Обобщим его на случай частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U. Полная энергия равна
Частицы. Обобщим его на случай частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U. Полная энергия равна  . Для случая движения в поле с потенциальной энергией мы должны подставить вместо E в (6) кинетическую энергию . Для случая движения в поле с потенциальной энергией мы должны подставить вместо E в (6) кинетическую энергию  и ур-е примет вид: и ур-е примет вид:
 На приведенные соображения следует смотреть как на соображения, поясняющие установление ур-ия Шредингера, а не как вывод его. Вообще это ур-е строго вывода не имеет, оно устанавливается, и правильность его подтверждается согласием с опытом получаемых с его помощью результатов.
Свидетельством квантового характера ур-я Шредингера явл. Присутствие в нём постоянной Планка
На приведенные соображения следует смотреть как на соображения, поясняющие установление ур-ия Шредингера, а не как вывод его. Вообще это ур-е строго вывода не имеет, оно устанавливается, и правильность его подтверждается согласием с опытом получаемых с его помощью результатов.
Свидетельством квантового характера ур-я Шредингера явл. Присутствие в нём постоянной Планка  . Ур-е Шредингера записывается в 2-х наиболее распространённых формах. . Ур-е Шредингера записывается в 2-х наиболее распространённых формах.
 - эта форма наиболее удобна для нахождения ф-ии
- эта форма наиболее удобна для нахождения ф-ии  как решение дифференциального ур-я. Другая форма записи: как решение дифференциального ур-я. Другая форма записи:
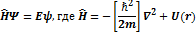 Более удобна для исследования принципиальных вопросов квантовой механики и обобщения ур-я Шредингера.
Еще есть ур-е Шредингера зависящее от времени:
Более удобна для исследования принципиальных вопросов квантовой механики и обобщения ур-я Шредингера.
Еще есть ур-е Шредингера зависящее от времени:
 Ур-е Шредингера имеет решение не при любых значениях Е, а лишь при некоторых, к-ые обозначаем
Ур-е Шредингера имеет решение не при любых значениях Е, а лишь при некоторых, к-ые обозначаем  . Значение Е при к-ых (1) имеет решение обладающее указанными свойствами, т.е. . Значение Е при к-ых (1) имеет решение обладающее указанными свойствами, т.е.  наз. собственными значениями, а функции наз. собственными значениями, а функции  явл. Решением ур-ия (1) при явл. Решением ур-ия (1) при  собственными ф-ями, принадлежащими собственным значениям собственными ф-ями, принадлежащими собственным значениям  .
Две собственные ф-ции, принадлежащие различным собственным значениям, ортогональны друг другу т.е. интеграл от произведения одной из этих ф-ций на ф-цию, комплексно сопряженную с другой, взятый по всей области интегрирования равен нулю. .
Две собственные ф-ции, принадлежащие различным собственным значениям, ортогональны друг другу т.е. интеграл от произведения одной из этих ф-ций на ф-цию, комплексно сопряженную с другой, взятый по всей области интегрирования равен нулю.
|
|
|



 .
.
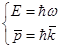 =>
=> 

 , где
, где  - оператор полной энергии системы (Гамильтона)
- оператор полной энергии системы (Гамильтона)

 , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность получения при измерении собственного значения
, с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность получения при измерении собственного значения  равна
равна  , где
, где 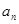 - коэффициенты разложения волновой функции
- коэффициенты разложения волновой функции 



 . Например
. Например 
 ;
;  ;
; 

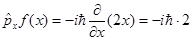

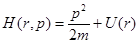 , где U(r) – потенциальная энергия
, где U(r) – потенциальная энергия

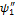 +
+ 
 = 0,
= 0,  + (2т/ћ2)(Е - Еп0)
+ (2т/ћ2)(Е - Еп0)  = 0. (26.10)
= 0. (26.10) +
+ 
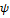 1(a) =
1(a) =  (a) =
(a) =  (a) (26.13)
(a) (26.13) = ћk1/
= ћk1/ 
 )у (y=k1a)• (26.19)
)у (y=k1a)• (26.19)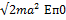 ) с синусоидой z = siny, а лишь те, которые согласуются со знаком в уравнении (26.18), т. е. точки пересечения в четных четвертях. Этим значениям уп, которых имеется конечное число, соответствуют энергии
) с синусоидой z = siny, а лишь те, которые согласуются со знаком в уравнении (26.18), т. е. точки пересечения в четных четвертях. Этим значениям уп, которых имеется конечное число, соответствуют энергии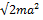 (26.20)
(26.20) = С2е-кх (26.21)
= С2е-кх (26.21) . Тогда проекция
. Тогда проекция  на какое-либо направление, в силу пространственного квантования, будет принимать
на какое-либо направление, в силу пространственного квантования, будет принимать 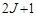 значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать
значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать 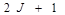 значение. Каждой ориентации магнитного момента
значение. Каждой ориентации магнитного момента  будет соответствовать своя энергия взаимодействия атома с магнитным полем:
будет соответствовать своя энергия взаимодействия атома с магнитным полем:  . В этом случае
. В этом случае  . Значит, возможны
. Значит, возможны  энергии взаимодействия. Таким образом, и полная энергия атома принимает
энергии взаимодействия. Таким образом, и полная энергия атома принимает  ;
;  ;
;  ;
; 
 . Энергия излучения, при переходе с одного уровня на другой, равна:
. Энергия излучения, при переходе с одного уровня на другой, равна: 
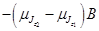 . Таким образом, изменение частоты
. Таким образом, изменение частоты  будет равно:
будет равно: 
 ,
,  .
.  .
. :
: 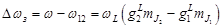 .
. , то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда
, то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда  . Для первого уровня
. Для первого уровня  , а
, а  . Таким образом, так как
. Таким образом, так как  , а
, а 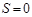 , то
, то  . Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление:
. Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление: .
. , где E0 – начальная энергия уровня до помещения его в магнитное поле.
, где E0 – начальная энергия уровня до помещения его в магнитное поле. 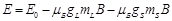 – запись через проекции
– запись через проекции  на
на  . Тогда
. Тогда  . Казалось бы, спектр должен быть очень богатым, ведь возможны
. Казалось бы, спектр должен быть очень богатым, ведь возможны  проекция
проекция  и ещё две проекции
и ещё две проекции 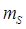 . Найдём его.
. Найдём его.  . Для одного уровня
. Для одного уровня 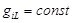 ,
,  :
:  ,
,  .
.  ;
;  . Тогда, если
. Тогда, если  и
и  ,
,  . Следовательно,
. Следовательно,  . Таким образом, может расщепляться на три компоненты:
. Таким образом, может расщепляться на три компоненты:  ;
;  . В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три.
. В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три.



 Модель Резерфорда, приписывала атому строение, аналогичное строению Солнечной системы: в центре находится положительно заряженное ядро, вокруг которого, подобно планетам, движутся электроны, удерживаемые у ядра силами кулоновского притяжения.. Резерфорд изучал движение тяжёлых положительно заряженных частиц в поле, создаваемом атомом.. Узкий пучок
Модель Резерфорда, приписывала атому строение, аналогичное строению Солнечной системы: в центре находится положительно заряженное ядро, вокруг которого, подобно планетам, движутся электроны, удерживаемые у ядра силами кулоновского притяжения.. Резерфорд изучал движение тяжёлых положительно заряженных частиц в поле, создаваемом атомом.. Узкий пучок  – частиц из источника излучения падала на тонкую золотую фольгу. За фольгой находилась поверхность, покрытая веществом, способным сцинтиллировать, например,
– частиц из источника излучения падала на тонкую золотую фольгу. За фольгой находилась поверхность, покрытая веществом, способным сцинтиллировать, например,  .
.  . Прицельным параметром
. Прицельным параметром  называется расстояние наименьшего сближения частиц, при отсутствии взаимодействия между ними (см. рис. 32)
называется расстояние наименьшего сближения частиц, при отсутствии взаимодействия между ними (см. рис. 32) (4).
(4).
 Последняя формула была получена Резерфордом и связывает угол рассеяния частицы с прицельным параметром
Последняя формула была получена Резерфордом и связывает угол рассеяния частицы с прицельным параметром  . Оставалось только проверить эту формулу. В опыте Резерфорд имел дело не с одной частицей, а с большим их числом. Частицы двигались под некоторыми углами, то есть имел место некоторый разброс углов. Частицы рассеивались на различных атомах и после рассеяния приобретали некоторые импульсы, значения которых также претерпевали некоторый разброс. Для того чтобы описать данный процесс, немыслимо пытаться рассчитывать траекторию движения каждой частицы. Полученная система уравнений будет слишком громоздка и практически неразрешима. В данном случае уместно прибегнуть к теории вероятностей. Введём понятие дифференциального поперечного сечения рассеяния
. Оставалось только проверить эту формулу. В опыте Резерфорд имел дело не с одной частицей, а с большим их числом. Частицы двигались под некоторыми углами, то есть имел место некоторый разброс углов. Частицы рассеивались на различных атомах и после рассеяния приобретали некоторые импульсы, значения которых также претерпевали некоторый разброс. Для того чтобы описать данный процесс, немыслимо пытаться рассчитывать траекторию движения каждой частицы. Полученная система уравнений будет слишком громоздка и практически неразрешима. В данном случае уместно прибегнуть к теории вероятностей. Введём понятие дифференциального поперечного сечения рассеяния  в угол между
в угол между  и
и  . Так будем называть отношение числа частиц dN
. Так будем называть отношение числа частиц dN  , рассеянных в единицу времени в угол
, рассеянных в единицу времени в угол  к полному потоку частиц
к полному потоку частиц  :
:  . Здесь
. Здесь  , где
, где  – полное число частиц. Все частицы, для которых
– полное число частиц. Все частицы, для которых  , будут рассеиваться в угол
, будут рассеиваться в угол 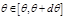 . Число частиц, прицельный параметр которых заключён в этом интервале, будет равно числу частиц, падающих на кольцо шириной db и радиусом внутренней окружности
. Число частиц, прицельный параметр которых заключён в этом интервале, будет равно числу частиц, падающих на кольцо шириной db и радиусом внутренней окружности  . Тогда
. Тогда  ,. Нам не важен здесь знак db, поэтому в дальнейшем будем рассматривать лишь его модуль. Воспользуемся теперь полученной нами формулой (4) для нахождения | db |:
,. Нам не важен здесь знак db, поэтому в дальнейшем будем рассматривать лишь его модуль. Воспользуемся теперь полученной нами формулой (4) для нахождения | db |:  .
. ,получим, ->
,получим, ->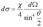 <- Последняя формула называется формулой Резерфорда. Перейдём теперь от плоского угла
<- Последняя формула называется формулой Резерфорда. Перейдём теперь от плоского угла  . Известно, что они связаны соотношением
. Известно, что они связаны соотношением  в сферической системе координат. Тогда если угол
в сферической системе координат. Тогда если угол 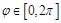 ,
,  . Из последней формулы выразим
. Из последней формулы выразим  ,
,  ;
;  , или
, или , то с помощью формул (4) и (5) можно вычислить зарядовое число Z. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа.
, то с помощью формул (4) и (5) можно вычислить зарядовое число Z. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа.
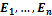 образуют дискретный ряд. В стационарных состояниях атомы не излучают.
2. При переходе атома из одного состояния с энергией
образуют дискретный ряд. В стационарных состояниях атомы не излучают.
2. При переходе атома из одного состояния с энергией  в другое с энергией
в другое с энергией  , происходит излучение, если
, происходит излучение, если  , или поглощение, если
, или поглощение, если  кванта света с частотой пропорциональной разности энергий состояний:
кванта света с частотой пропорциональной разности энергий состояний:  .
Бор ввёл также правила, в соответствии с которыми определяются стационарные состояния атомных систем. Данные правила получили название правил квантования. Бор предположил, что стационарными являются лишь те состояния, в которых момент импульса электрона равен целому числу постоянных Планка:
.
Бор ввёл также правила, в соответствии с которыми определяются стационарные состояния атомных систем. Данные правила получили название правил квантования. Бор предположил, что стационарными являются лишь те состояния, в которых момент импульса электрона равен целому числу постоянных Планка:  . Коэффициент пропорциональности между моментом импульса электрона и постоянной Планка называют главным квантовым числом.
Р-им водородоподобный атом, который представляет собой систему из ядра и одного электрона. Масса ядра много больше массы электрона, поэтому ядро можно считать неподвижным. Для простоты положим, что электрон движется вокруг ядра с зарядом Z по круговой орбите радиусаr. Со стороны ядра на электрон действует кулоновская сила притяжения, сообщая ему центростремительное ускорение
. Коэффициент пропорциональности между моментом импульса электрона и постоянной Планка называют главным квантовым числом.
Р-им водородоподобный атом, который представляет собой систему из ядра и одного электрона. Масса ядра много больше массы электрона, поэтому ядро можно считать неподвижным. Для простоты положим, что электрон движется вокруг ядра с зарядом Z по круговой орбите радиусаr. Со стороны ядра на электрон действует кулоновская сила притяжения, сообщая ему центростремительное ускорение
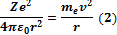 Потенциальная энергия электрона в поле ядра
Потенциальная энергия электрона в поле ядра
 А его полная энергия:
А его полная энергия:
 Момент импульса электрона, вращающегося на n-й орбите, равен:
Момент импульса электрона, вращающегося на n-й орбите, равен:
 Исключая из (2) и (6)
Исключая из (2) и (6)  ,получим для радиуса n-й орбиты
,получим для радиуса n-й орбиты
 Радиус первой боровской орбиты в атоме водорода (n=1, Z=1) равен
Радиус первой боровской орбиты в атоме водорода (n=1, Z=1) равен
 И называется первым боровским радиусом.
Из выр-ий (4) и (7) сразу получается значение энергии электрона, находящегося на n-й орбите:
И называется первым боровским радиусом.
Из выр-ий (4) и (7) сразу получается значение энергии электрона, находящегося на n-й орбите:
 Из (1) и (9), можно получить частоты спектральных линий, возникающих при переходе электрона с одной орбиты на другую:
Из (1) и (9), можно получить частоты спектральных линий, возникающих при переходе электрона с одной орбиты на другую:
 Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины
Формула выражает собой закон, которому подчиняется процесс лучеиспускания водородоподобных атомов. Величины 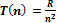 называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов.
называются спектральными термами. Частота спектральных линий является разностью ее нижнего и верхнего термов.
 Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
Общая формула Бальмера для частот спектральных линий:
Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца.
Общая формула Бальмера для частот спектральных линий:
 –ультрафиолетовая область;
-серия Бальмера (
–ультрафиолетовая область;
-серия Бальмера ( –видимая область;
-серия Пашена (
–видимая область;
-серия Пашена ( –инфракрасная область;
-серия Брэкета (
–инфракрасная область;
-серия Брэкета ( –инфракрасная область;
-серия Пфунда (
–инфракрасная область;
-серия Пфунда ( –инфракрасная область;
–инфракрасная область;
 где m=1, 2, 3…. Впоследствии были открыты и остальные серии для атома водорода:
где m=1, 2, 3…. Впоследствии были открыты и остальные серии для атома водорода:



 Расстояния между спектральными линиями с увеличением числа m становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий:
Расстояния между спектральными линиями с увеличением числа m становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий:
 Причём n определяет номер спектральной серии.
Причём n определяет номер спектральной серии.  для спектра испускания;
для спектра испускания; 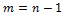 для спектра поглощения. Введём
для спектра поглощения. Введём  Таким образом, частота любой спектральной линии определяется
Таким образом, частота любой спектральной линии определяется  Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой:
Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой:
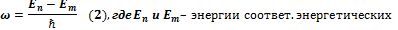 уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае
уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае  В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.
Изотопами наз. элементы, заряд ядра к-ых одинаков, а массы различны. Химические св-ва изотопов весьма близки др. к др.
Дейтрон – ядро атома дейтерия, состоит из протона и нейтрона. Тритон – ядро атома трития, состоит из протона и 2-х нейтронов. Различие в массах ядер различных изотопов приводит к сдвигу линий др. относительно др. в их спектрах излучения – изотопический сдвиг. Он не велик. Например для
В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.
Изотопами наз. элементы, заряд ядра к-ых одинаков, а массы различны. Химические св-ва изотопов весьма близки др. к др.
Дейтрон – ядро атома дейтерия, состоит из протона и нейтрона. Тритон – ядро атома трития, состоит из протона и 2-х нейтронов. Различие в массах ядер различных изотопов приводит к сдвигу линий др. относительно др. в их спектрах излучения – изотопический сдвиг. Он не велик. Например для
 По сдвигу этих линий можно определить массу изотопа, по интенсивности – концентрацию изотопа.
По сдвигу этих линий можно определить массу изотопа, по интенсивности – концентрацию изотопа.
 Из соотношений между импульсом и энергией ньютоновской
Из соотношений между импульсом и энергией ньютоновской  Воспользуемся квантовыми соотношениями для энергии и составляющих импульса:
Воспользуемся квантовыми соотношениями для энергии и составляющих импульса:
 Подставляя их в (1), сокращая на
Подставляя их в (1), сокращая на  получим:
получим:
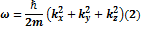 - закон дисперсии волн де Бройля в нерелятивистском приближении. Далее возьмем формулу плоской волны де Бройля и продифференцировав ее 1 раз во времени и 2 по всеми координатам получим:
- закон дисперсии волн де Бройля в нерелятивистском приближении. Далее возьмем формулу плоской волны де Бройля и продифференцировав ее 1 раз во времени и 2 по всеми координатам получим:
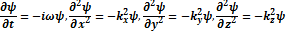 Найдя отсюда
Найдя отсюда  и подставив в закон дисперсии (2):
и подставив в закон дисперсии (2):

 Для стоячих монохроматических волн решение может быть представлено в виде произведения 2-х ф-ий, одна из к-ых ф-ия координат, другая - ф-ия времени, зависимость от времени
Для стоячих монохроматических волн решение может быть представлено в виде произведения 2-х ф-ий, одна из к-ых ф-ия координат, другая - ф-ия времени, зависимость от времени  .Для таких решений левая часть (3) дает:
.Для таких решений левая часть (3) дает:

 Частицы. Обобщим его на случай частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U. Полная энергия равна
Частицы. Обобщим его на случай частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U. Полная энергия равна  . Для случая движения в поле с потенциальной энергией мы должны подставить вместо E в (6) кинетическую энергию
. Для случая движения в поле с потенциальной энергией мы должны подставить вместо E в (6) кинетическую энергию  и ур-е примет вид:
и ур-е примет вид:
 На приведенные соображения следует смотреть как на соображения, поясняющие установление ур-ия Шредингера, а не как вывод его. Вообще это ур-е строго вывода не имеет, оно устанавливается, и правильность его подтверждается согласием с опытом получаемых с его помощью результатов.
Свидетельством квантового характера ур-я Шредингера явл. Присутствие в нём постоянной Планка
На приведенные соображения следует смотреть как на соображения, поясняющие установление ур-ия Шредингера, а не как вывод его. Вообще это ур-е строго вывода не имеет, оно устанавливается, и правильность его подтверждается согласием с опытом получаемых с его помощью результатов.
Свидетельством квантового характера ур-я Шредингера явл. Присутствие в нём постоянной Планка  . Ур-е Шредингера записывается в 2-х наиболее распространённых формах.
. Ур-е Шредингера записывается в 2-х наиболее распространённых формах.
 - эта форма наиболее удобна для нахождения ф-ии
- эта форма наиболее удобна для нахождения ф-ии  как решение дифференциального ур-я. Другая форма записи:
как решение дифференциального ур-я. Другая форма записи:
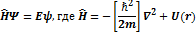 Более удобна для исследования принципиальных вопросов квантовой механики и обобщения ур-я Шредингера.
Еще есть ур-е Шредингера зависящее от времени:
Более удобна для исследования принципиальных вопросов квантовой механики и обобщения ур-я Шредингера.
Еще есть ур-е Шредингера зависящее от времени:
 Ур-е Шредингера имеет решение не при любых значениях Е, а лишь при некоторых, к-ые обозначаем
Ур-е Шредингера имеет решение не при любых значениях Е, а лишь при некоторых, к-ые обозначаем  . Значение Е при к-ых (1) имеет решение обладающее указанными свойствами, т.е.
. Значение Е при к-ых (1) имеет решение обладающее указанными свойствами, т.е.  явл. Решением ур-ия (1) при
явл. Решением ур-ия (1) при  собственными ф-ями, принадлежащими собственным значениям
собственными ф-ями, принадлежащими собственным значениям 


