
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Маг и мех моменты электрона. Правило квантования.Содержание книги Поиск на нашем сайте
Итак, электрон обладает в атоме четырьмя моментами: 1.Механическим (орбитальным и спиновым); 2. Полный механический момент импульса электрона является векторной суммой орбитального механического момента и спинового механического момента: Полный магнитный момент электрона равен сумме векторов орбитального магнитного момента и спинового магнитного момента:
26. Маг и мех момент атома. Векторная модель атома. Jj и L-S связь…
Рассмотри случай изолированного атома. В изолированном атоме L j=const. Если вектор L j сохраняет своё направление в пространстве, вектора Найдём связь между
Подставим значения для каждого момента, выраженное через квантовые числа: Выражение, помещённое в круглых скобках, называется фактором Ланде: L-S связь. Реализуется в том случае, если электростатическое взаимодействие между электронами в атоме сильнее, чем спин-орбитальное взаимодействие для каждого электрона. Поэтому сначала находятся полный орбитальный и полный спиновой моменты для каждого электрона, которые потом складываются:
2. J-J связь Этот тип связи реализуется, когда спин-орбитальное взаимодействие в атоме сильнее, чем электростатическое взаимодействие различный электронов друг с другом. Поэтому мы находим сначала полный механический момент всех электронов, а потом – полный момент всего атома как векторную сумму всех полных моментов каждого электрона: Отношение μ/L модуля магнитного момента к модулю механического момента, выраженное в единицах e/2m, называется гиромагнитным отношением: μ/L= e/2m =g. Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е. gl=1. Для собственного магнитного момента электрона, обусловленного наличием спина: μ s= eLs/m. Тогда гиромагнитное отношение для спинового магнитного момента и механического момента gs=2.
Эффект Зеемана. Как известно, полный механический момент атома
Каждый из возможных переходов приводит к излучению отдельной линии. Явление расщепления спектральных линий при помещении атома в слабое внешнее магнитное поле называют аномальным (сложным) эффектом Зеемана. Полная энергия равна, как было записано выше: Определим величину смещения частоты при эффекте Зеемана Если величина зеемановского расщепления равна частоте ланморовой прецессии,
Такой эффект называют простым (нормальным) эффектом Зеемана. Так как поле слабое, расщепление Зеемана будет меньше естественного (мультиплетного) расщепления, вызванного спин-орбитальным взаимодействием. 29. Эффект Пашена – Бака. Рассмотрим теперь случай, когда индукция магнитного поля велика. В данной ситуации энергия взаимодействия магнитного момента атома с полем становится больше спин-орбитального взаимодействия и связь между спиновыми и орбитальными моментами разрушается. Каждый в отдельности начинает взаимодействовать с полем. Это явление разрыва спин-орбитальной связи в магнитном поле называется эффектом Пашена – Бака. Энергия уровня, в данном случае, равна:
Рентгеновские спектры. Рентгеновские спектры бывают двух видов: сплошные и линейчатые. Сплошные спектры возникают при торможении быстрых эл-нов в вещ-ве антикатода и являются обычным тормозным излучением эл-нов. Линейчатый спектр состоит из отдельных линий излучения. Он зависит от материала антикатода и полностью характеризуется им. Каждый эл-т обладает характерным для него линейчатым спектром. Между рентгеновскими линейными спектрами и оптическими линецчатыми спектрами существует три различия. Во-первых, частота рентгеновского излучения во много раз больше оптического. Значит энергия рентгеновского кванта в тысячи раз больше энергии оптического кванта. Во-вторых, рентгеноспектры различных эл-тов имеют одинаковую структуру, тогда так структура оптических спектров различных эл-тов существенно различается. В-третьих оптические спектры поглощения состоят из отдельных линий, совпадающих с линиями излучения главной серии соответств эл-та. Рентгеновские спектры поглощения не похожи на рентгеновские спектры испускания: они состоят из нескольких полос с резким длинноволновым краем. Объяснение: эл-н, падающий на материал антикатода, сталкиваясь с атомами антикатодо, может выбить эл-н с одной из внутренних оболочек атома. Эл-ны более внешних оболочек могут переходить на свободное место. В результате оспускается квант рентгеновского излучения. Энергия эл-на в кулоновском поле ядра:
Энергия эл-на на одной из внутренних оболочек:
При переходе эл-на на освободившееся место на внутренней оболочке с внешней оболочки излучается квант с частотой:
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.42.61 (0.007 с.) |

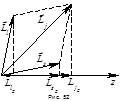 Магнитным (орбитальным и спиновым).
Магнитным (орбитальным и спиновым). . Так как модули каждого момента всегда квантуются:
. Так как модули каждого момента всегда квантуются: 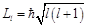 ,
, 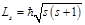 то и их сумма должна квантоваться:
то и их сумма должна квантоваться: 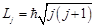 , где
, где 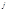 – квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось Z:
– квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось Z: 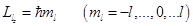 –
–  значение;
значение;  . Тогда
. Тогда 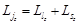 ;
; 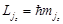 , где
, где  –
– 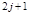 значение. Так как
значение. Так как 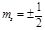 , то тогда
, то тогда 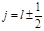 . Определим угол между орбитальным и спиновым моментами электрона. Так как
. Определим угол между орбитальным и спиновым моментами электрона. Так как 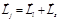 , то, возводя это выражение в квадрат, получим:
, то, возводя это выражение в квадрат, получим: 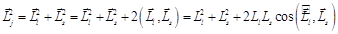 . Отсюда
. Отсюда 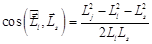 , или
, или 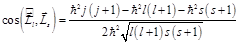 . Так как возможно лишь
. Так как возможно лишь 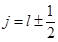 – 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).
– 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).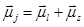 . Так как
. Так как  . Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.
. Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.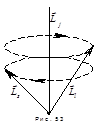
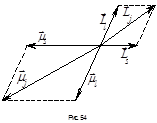
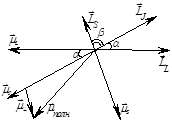 Полный маг момент атома складывается из полных спинового и орбитального моментов атома:
Полный маг момент атома складывается из полных спинового и орбитального моментов атома: 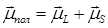 . Для каждого из них мы можем записать:
. Для каждого из них мы можем записать: 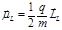 и
и 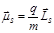 . Таким образом, полный механический момент не будет лежать на одной оси с полным механическим моментом.
. Таким образом, полный механический момент не будет лежать на одной оси с полным механическим моментом.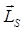 и
и 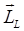 должны прецессировать вокруг
должны прецессировать вокруг  .
. 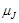 и
и 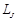 . Из рисунка видно, что
. Из рисунка видно, что  (1).
(1). 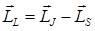 (2),
(2), 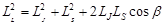 . Следовательно,
. Следовательно, 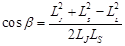 . Найдём cos(α). Из уравнения (2) следует, что
. Найдём cos(α). Из уравнения (2) следует, что  ,
, 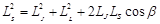 ;
;  . Запишем уравнения для проекции магнитного момента на направление вектора
. Запишем уравнения для проекции магнитного момента на направление вектора 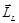 :
: 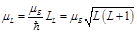 :
: 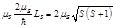 Подставим последние два выражения в (1) с учётом полученных выше выражений для косинусов:
Подставим последние два выражения в (1) с учётом полученных выше выражений для косинусов: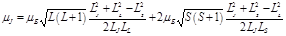

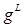 . Таким образом,
. Таким образом,  (3). Выражение (3) аналогично тому, которое связывает спиновой орбитальный момент с орбитальным механическим. Из этой аналогии следует смысл фактора Ланде – это гиромагнитное отношение для полного магнитного момента.
(3). Выражение (3) аналогично тому, которое связывает спиновой орбитальный момент с орбитальным механическим. Из этой аналогии следует смысл фактора Ланде – это гиромагнитное отношение для полного магнитного момента. .Полный момент, очевидно, квантуется:
.Полный момент, очевидно, квантуется: 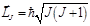 , где
, где 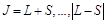 . Как было показано выше, число способов, которыми складываются моменты, равно числу слагаемых:
. Как было показано выше, число способов, которыми складываются моменты, равно числу слагаемых:  , то есть возможно
, то есть возможно 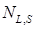 состояний атома. Обычно бывает S < L. Тогда
состояний атома. Обычно бывает S < L. Тогда 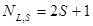 .
.  определяет спин-орбитальное расщепление энергетических уровней в атоме и называется мультиплетностью.
определяет спин-орбитальное расщепление энергетических уровней в атоме и называется мультиплетностью.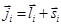 ,
, 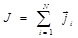 . Этот тип связи реализуется для многоэлектронных атомов (окончание таблицы Менделеева).
. Этот тип связи реализуется для многоэлектронных атомов (окончание таблицы Менделеева). . Тогда проекция
. Тогда проекция  на какое-либо направление, в силу пространственного квантования, будет принимать
на какое-либо направление, в силу пространственного квантования, будет принимать 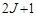 значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать
значение. Так как проекция магнитного момента связана с проекцией механического момента через магнетон Бора, то и проекция магнитного момента тоже может принимать 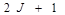 значение. Каждой ориентации магнитного момента
значение. Каждой ориентации магнитного момента  будет соответствовать своя энергия взаимодействия атома с магнитным полем:
будет соответствовать своя энергия взаимодействия атома с магнитным полем:  . В этом случае
. В этом случае  . Значит, возможны
. Значит, возможны  энергии взаимодействия. Таким образом, и полная энергия атома принимает
энергии взаимодействия. Таким образом, и полная энергия атома принимает  ;
;  ;
;  ;
; 
 . Энергия излучения, при переходе с одного уровня на другой, равна:
. Энергия излучения, при переходе с одного уровня на другой, равна: 
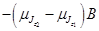 . Таким образом, изменение частоты
. Таким образом, изменение частоты  будет равно:
будет равно: 
 ,
,  .
.  .
. :
: 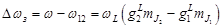 .
. , то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда
, то такое расщепление называют нормальным зеемановским расщеплением. Этот эффект имеет место в том случае, когда  . Для первого уровня
. Для первого уровня  , а
, а  . Таким образом, так как
. Таким образом, так как  , а
, а 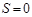 , то
, то  . Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление:
. Следовательно, для синглетных уровней. В слабом магнитном поле наблюдается нормальное зеемановское расщепление: .
. , где E0 – начальная энергия уровня до помещения его в магнитное поле.
, где E0 – начальная энергия уровня до помещения его в магнитное поле. 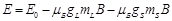 – запись через проекции
– запись через проекции  на
на  . Тогда
. Тогда  . Казалось бы, спектр должен быть очень богатым, ведь возможны
. Казалось бы, спектр должен быть очень богатым, ведь возможны  проекция
проекция  и ещё две проекции
и ещё две проекции 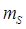 . Найдём его.
. Найдём его.  . Для одного уровня
. Для одного уровня 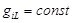 ,
,  :
:  ,
,  .
.  ;
;  . Тогда, если
. Тогда, если  и
и  ,
,  . Следовательно,
. Следовательно,  . Таким образом, может расщепляться на три компоненты:
. Таким образом, может расщепляться на три компоненты:  ;
;  . В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три.
. В эффекте Зеемана расщепление может быть только для синглетных термов. В эффекте Пашена – Бака любой терм расщепляется на три.





