
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция одиночных электроновСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В опытах Дэвиссона и Джермера интенсивность электронных пучков была велика. Возникает вопрос, появится ли дифракционная картина в случае, если электроны проходят через экспериментальную установку, например, кристалл, представляющий собой дифракционную решетку, поодиночке (аналогично одиночным фототонам в (лекция N 5, § 3). Опыт с одиночными электронами выполнили в 1949 г. советские физики Л. М. Биберман, Н. Г. Сушкин и В. А. Фабрикант. Они наблюдали дифракционную картину электронного пучка от мелкокристаллического тела. Разумеется, один электрон не даст сразу интерференционной картины, он будет просто зафиксирован целиком в определенном месте пространства. Но с течением времени, как показал опыт, формируется такая же дифракционная картина, как и при большой интенсивности пучка. Следовательно, волновые свойства нельзя объяснить взаимодействием различных электронов в интенсивном пучке, они присущи каждому одиночному электрону.
Рис. 6.2 Мы рассмотрим идеализацию действительного опыта - мысленный экспериментпо дифракции электронов на двух щелях. Схема этого мысленного эксперимента такая же как и у опыта Юнга по интерференции света (см. рис. 6.2). Электронный пучок направляется на непрозрачный экран с двумя щелями, расположенными на расстоянии d друг от друга. Электроны фиксируются маленькими счетчиками, размером в Δx, расположенными вдоль экрана наблюдения. При интенсивном пучке электронов графиком зависимости числа срабатываний счетчиков от координаты x будет интерференционная кривая: чередование максимумов и минимумов (точнее, ступенчатая функция - гистограмма, но при малых Δx ее ступенчатость будет мала). Что будет происходить в этой установке, если электроны будут проходить ее поодиночке? Как показывает опыт с течением времени сформируется точно такая же интерференционная картина как и с интенсивным пучком электронов. Как можно объяснить появление этой интерференционной картины? Электрон неделим, он всегда регистрируется целиком. Значит дебройлевская волна каждого электрона проходит одновременно через оба отверстия, затем волны, идущие от отверстий 1 и 2, интерферируют друг с другом. Электроны чаще попадают в те места экрана, где интенсивность результирующей волны больше. Здесь ситуация аналогична той, что была разобрана нами в предыдущей лекции для случая интерференции одиночных фотонов. Волновая функция и волна де Бройля Дальнейшее развитие физики показало, что волна де Бройля - частный случай более общего фундаментального понятия квантовой физики - волновой функции, которую обозначают греческой буквой Ψ, ("пси"). В общем случае волновая функция - это комплексная функция координат и времени. Подробнее с волновой функцией мы познакомимся при изучении дифференциального уравнения - уравнения Шредингера, решением которого является волновая функция. Волновая функция свободно движущейся частицы с точно заданным импульсом p и является волной де Бройля. В частном случае движения вдоль оси х она имеет вид плоской волны:
здесь А - нормировочная постоянная; E - энергия частицы; p - ее импульс; e = 2,73... - основание натуральных логарифмов; В 1926 г. Макс Борн дал вероятностную интерпретацию волновой функции Ψ, согласно которой квадрат модуля волновой функции |Ψ|2 определяет вероятность dw того, что микрообъект будет обнаружен в пределах объема dV, т.е.
Здесь На функцию Ψ накладывается условие нормировки, которое следует из того, что полная вероятность w обнаружить частицу в любом месте доступного ей пространства должна быть равна единице, т.е.:
Подставляя сюда dw, получим условие нормировки для волновой функции Ψ:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.22 (0.01 с.) |



 - мнимая единица.
- мнимая единица.
 - это комплексно-сопряженная функция, которая отличается от Ψ тем, что мнимую единицу i заменяют на -i. Напомним, что
- это комплексно-сопряженная функция, которая отличается от Ψ тем, что мнимую единицу i заменяют на -i. Напомним, что 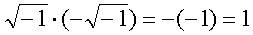 , таким образом, вероятность dw будет определяться, как и требуется, положительным числом.
, таким образом, вероятность dw будет определяться, как и требуется, положительным числом.




