

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Дифракция на круглом отверстии.
Похожие статьи вашей тематики
Дифракционную картину Фраунгофера от круглого отверстия в преграде можно наблюдать на экране в фокальной плоскости линзы, направив на отверстие нормально плоскую световую волну. Картина имеет вид центрального светлого пятна, окружённого чередующимися тёмными и светлыми кольцами. Минимум первого тёмного кольца отстаёт от центра дифракционной картины на угловое расстояние  (если апертура больше длины волны). размер дифракционной картины тем меньше, чем больше диметр отверстия D. подавляющая часть светового потока попадает в область центрального светлого пятна – диск Эйри. Пусть плоская волна падает на круглое отверстие радиусом ρ.Дифракция света на круглом отверстии. Координатные оси в области источников и в области дифракции: (если апертура больше длины волны). размер дифракционной картины тем меньше, чем больше диметр отверстия D. подавляющая часть светового потока попадает в область центрального светлого пятна – диск Эйри. Пусть плоская волна падает на круглое отверстие радиусом ρ.Дифракция света на круглом отверстии. Координатные оси в области источников и в области дифракции: 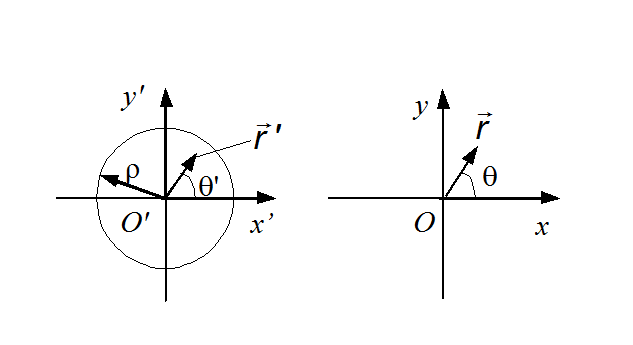
 ,следует, что ,следует, что 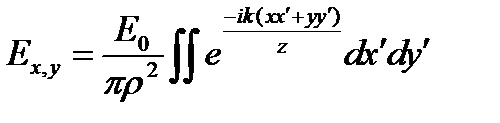 . В полярной системе координат . В полярной системе координат 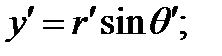  , ,   , ,  , следовательно: , следовательно:
 . Второй интеграл равен . Второй интеграл равен  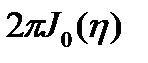 , где , где  - функция Бесселя нулевого порядка - функция Бесселя нулевого порядка  Тогда Тогда  Из теории функций Бесселя: Из теории функций Бесселя:  где где  — функция Бесселя первого порядка. Поэтому — функция Бесселя первого порядка. Поэтому  и и  . Радиус 1-го тёмного кольца определяется из условия: . Радиус 1-го тёмного кольца определяется из условия: 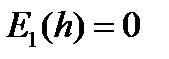 . Угол, под которым это кольцо видно из центра круглого отверстия: . Угол, под которым это кольцо видно из центра круглого отверстия: 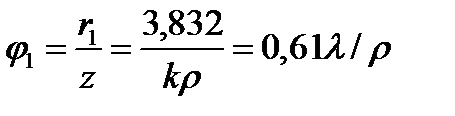 . Угловой размер светлого пятна: . Угловой размер светлого пятна:  . Второе и третье тёмное пятно наблюдаются под углами: . Второе и третье тёмное пятно наблюдаются под углами: 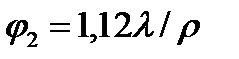 и и  . .
3.7. Дифракционная решётка. Рассмотрим упорядоченную структуру, состоящую из N одинаковых параллельных щелей, ширины b, разделённых непрозрачными промежутками, имеющих ширину a. Такая структура представляет собой одномерную (линейную) дифракционную решётку. d = a + b - период решётки. К определению разности хода при дифракции света на одномерной решётке:
 Разность хода: ΔL =dsinφ, Сдвиг фаз: Разность хода: ΔL =dsinφ, Сдвиг фаз:  . Амплитуда волны создаваемой щелью вследствие дифракции: . Амплитуда волны создаваемой щелью вследствие дифракции:  , где , где 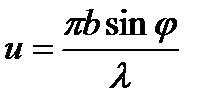 . Фазу волны, создаваемой первой щелью положим равной нулю. Тогда её амплитуда будет равна: . Фазу волны, создаваемой первой щелью положим равной нулю. Тогда её амплитуда будет равна:
 . Комплексные амплитуды, волн создаваемых последующими щелями, будут равны: . Комплексные амплитуды, волн создаваемых последующими щелями, будут равны:  , , 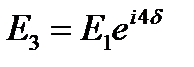 , …………………., , ………………….,  . Амплитуда результирующего поля: . Амплитуда результирующего поля:  , ,  . Амплитуда результирующей волны: . Амплитуда результирующей волны:  . Интенсивность результирующей волны: . Интенсивность результирующей волны:  , ,  - характеризует распределение интенсивности при дифракции света на каждой из щелей. - характеризует распределение интенсивности при дифракции света на каждой из щелей.  - учитывает взаимную интерференцию волн, создаваемых N щелями. Условия интерференционных максимумов: dsinφ=mλ (4). Выражение (4) называется условием главных максимумовпри дифракции на решётке. Числа m=0, - учитывает взаимную интерференцию волн, создаваемых N щелями. Условия интерференционных максимумов: dsinφ=mλ (4). Выражение (4) называется условием главных максимумовпри дифракции на решётке. Числа m=0,  1, 1,  2,… определяют порядок дифракционных максимумов. При j=0 и m =0 следует, что I(0) = N2 I0. Условие минимумов. Минимумы при дифракции на решётке из N щелей: bsin j =m ¢l. (5) Полученные минимумы называются прежними минимумами, Условие (5) называется условием прежних минимумов.Условия дополнительных минимумов: 2,… определяют порядок дифракционных максимумов. При j=0 и m =0 следует, что I(0) = N2 I0. Условие минимумов. Минимумы при дифракции на решётке из N щелей: bsin j =m ¢l. (5) Полученные минимумы называются прежними минимумами, Условие (5) называется условием прежних минимумов.Условия дополнительных минимумов: 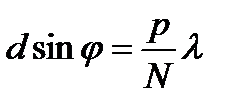 , где p= 1, 2,..., N -1, N+ 1,.... p =0 и p=N, p=2N,... образуют главные максимумы, поэтому они исключаются из условия дополнительных минимумов. bsinj=m ¢ ¢ l, где , где p= 1, 2,..., N -1, N+ 1,.... p =0 и p=N, p=2N,... образуют главные максимумы, поэтому они исключаются из условия дополнительных минимумов. bsinj=m ¢ ¢ l, где  . Условия дополнительных минимумов: . Условия дополнительных минимумов: 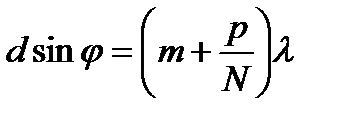 , где P= 1,2,3,... N -1. P – номер дополнительного дифракционного минимума, отсчитанного от ближайшего слева максимума.Наклонное падение плоской волны на решётку: Разность хода волн, дифрагирующих под углом φ: Δ=d* * , где P= 1,2,3,... N -1. P – номер дополнительного дифракционного минимума, отсчитанного от ближайшего слева максимума.Наклонное падение плоской волны на решётку: Разность хода волн, дифрагирующих под углом φ: Δ=d* *  , где Θ – угол падения волны на решётку. Условие главных максимумов: , где Θ – угол падения волны на решётку. Условие главных максимумов: 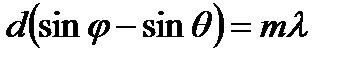 или или 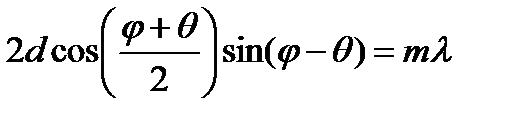 (10), где (10), где 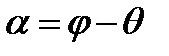 - угол отклонения лучей от первоначального направления. Выражение (10) можно представить в виде: - угол отклонения лучей от первоначального направления. Выражение (10) можно представить в виде:  , где , где  и и  . Если угол падения Θ является большим (Θ → . Если угол падения Θ является большим (Θ → 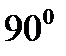 ), то d¢ <<d. ), то d¢ <<d.
3.9. Фазовые решётки. Решетки, в которых плоскость каждой щели совпадает с плоскостью решетки и, следовательно, не возникает никакой разности фаз при прохождении плоской волны через решетку, называются амплитудными.  Фазовая решетка, работающая на пропускании (а) и отражении (б) света. Решётки, принцип действия которых основан на измерении фазы, называются фазовыми решётками. Примером фазовой решётки является отражательная решётка с профилированным штрихом. Фазовая решетка, работающая на пропускании (а) и отражении (б) света. Решётки, принцип действия которых основан на измерении фазы, называются фазовыми решётками. Примером фазовой решётки является отражательная решётка с профилированным штрихом.  Разность хода: Разность хода:  , где q - угол падения, j - угол дифракции. Угол падения света на плоскость штриха будет равен , где q - угол падения, j - угол дифракции. Угол падения света на плоскость штриха будет равен  , угол отражения - , угол отражения -  . Тогда . Тогда  , откуда , откуда  , следовательно , следовательно  . Главные максимумы: . Главные максимумы:  или или  . Порядок дифракционного спектра: . Порядок дифракционного спектра:  или или  ,где h – высота профиля штриха. Если, например ,где h – высота профиля штриха. Если, например  , то для решётки будет второй дифракционный максимум. Распределение интенсивности сдвинется относительно распределения , то для решётки будет второй дифракционный максимум. Распределение интенсивности сдвинется относительно распределения  , для которого главный максимум наблюдается при , для которого главный максимум наблюдается при  . Синусоидальная решётка Релея. Рассмотрим прохождение плоской волны E0 через периодическую структуру, коэффициент пропускания которой характеризуется гармонической функцией: . Синусоидальная решётка Релея. Рассмотрим прохождение плоской волны E0 через периодическую структуру, коэффициент пропускания которой характеризуется гармонической функцией:  где 0< р <1, g≤0,5. Вид функции пропускания для решетки со штрихами (а) и синусоидальной решетки Рэлея: где 0< р <1, g≤0,5. Вид функции пропускания для решетки со штрихами (а) и синусоидальной решетки Рэлея:
 Поле за решёткой будет иметь вид: Поле за решёткой будет иметь вид:  , ,
 . Определим поле создаваемое одним (первым) периодом: . Определим поле создаваемое одним (первым) периодом:  . Поскольку . Поскольку  , то , то 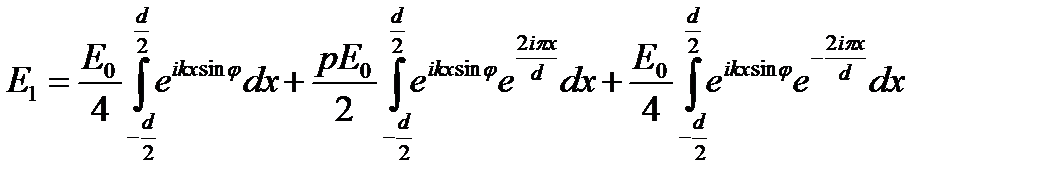 , ,  . Интенсивность, создаваемая всей решёткой, имеющей N периодов: . Интенсивность, создаваемая всей решёткой, имеющей N периодов: 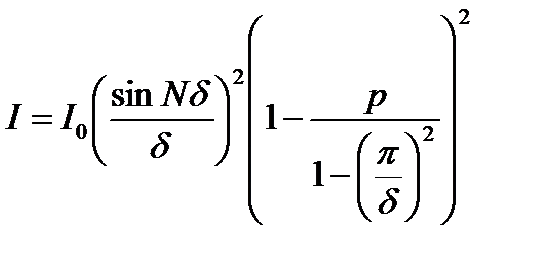 (16). При (16). При  имеем sinN d=0. При m =0, m =1 и m =-1 при раскрытии неопределённости в (16) получаются максимумы интенсивности. Решётка Релея даёт только три максимума: нулевой при m=0 и два максимума в первых порядках при m =±1. имеем sinN d=0. При m =0, m =1 и m =-1 при раскрытии неопределённости в (16) получаются максимумы интенсивности. Решётка Релея даёт только три максимума: нулевой при m=0 и два максимума в первых порядках при m =±1.
3.10 Основные характеристики спектральных приборов. Спектральные приборы выполняют физическое разложение излучения на монохроматические составляющие. Математически это выполняется с помощью преобразования Фурье. Спектральные приборы по назначению делятся на несколько типов: спектрографы, спектрофотометры и монохроматоры. Аппаратная функция. Идеальный спектральный прибор — прибор,  который не вносит искажения в распр. энергии спектральной линии, попадающей на входную щель. Реальные приборы вносят изменения и приводят к уширению спектральных линий. Основные причины— дифракция света на вх. щели, которая имеет конечную ширину, аберрации опт. элементов прибора, влияние с-мы регистрации. Совокупное действие спектрального прибора характеризуется аппаратной функцией который не вносит искажения в распр. энергии спектральной линии, попадающей на входную щель. Реальные приборы вносят изменения и приводят к уширению спектральных линий. Основные причины— дифракция света на вх. щели, которая имеет конечную ширину, аберрации опт. элементов прибора, влияние с-мы регистрации. Совокупное действие спектрального прибора характеризуется аппаратной функцией  . Аппаратная функция представляет отклик прибора на . Аппаратная функция представляет отклик прибора на  узкий монохром. импульс. Если направить на вход спектрального прибора монохром. излучение, то регистрируемая линия и будет аппаратной функцией. Чем более узкая инструментальная функция, тем меньше искажений вносит прибор. Аппаратная функция искажает регистрируемый спектр. Пусть спектральная плотность излучения задается функцией узкий монохром. импульс. Если направить на вход спектрального прибора монохром. излучение, то регистрируемая линия и будет аппаратной функцией. Чем более узкая инструментальная функция, тем меньше искажений вносит прибор. Аппаратная функция искажает регистрируемый спектр. Пусть спектральная плотность излучения задается функцией  . После прохожд. через спектральный прибор каждой длине волны соответствует опр. координата на его фокальной плоскости. Поэтому функции . После прохожд. через спектральный прибор каждой длине волны соответствует опр. координата на его фокальной плоскости. Поэтому функции  будет соответствовать будет соответствовать  . Найдем распр. F(x), которое зарегистрирует спектральный прибор, имеющий аппаратную функцию f(x). Выделим в спектре . Найдем распр. F(x), которое зарегистрирует спектральный прибор, имеющий аппаратную функцию f(x). Выделим в спектре  монохроматическую компоненту, интенсивность которой монохроматическую компоненту, интенсивность которой  представлена заштрихованным прямоугольником Его ширина dx очень малая. Прибор с апп. функцией представлена заштрихованным прямоугольником Его ширина dx очень малая. Прибор с апп. функцией 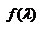 размазывает этот участок в распределение размазывает этот участок в распределение  . интенсивность, заключенная в нем сохраняется, т.к. апп. функция нормирована по площади к единице. . интенсивность, заключенная в нем сохраняется, т.к. апп. функция нормирована по площади к единице.  , ,  . Определим значение наблюдаемого распределения F(х') в точке х'. Доля монохром. компоненты, попавшая в точку х', за счет «размазывания» равна произведению апп. функции в этой точке на величину интенсивности линии в этой точке . Определим значение наблюдаемого распределения F(х') в точке х'. Доля монохром. компоненты, попавшая в точку х', за счет «размазывания» равна произведению апп. функции в этой точке на величину интенсивности линии в этой точке  . Другие монохром. компоненты также дадут вклад в наблюдаемое значение функции в точке x'. В итоге наблюдаемое распр. выразится сверткой функции f(x) и I(x): . Другие монохром. компоненты также дадут вклад в наблюдаемое значение функции в точке x'. В итоге наблюдаемое распр. выразится сверткой функции f(x) и I(x):  - это позволяет находить функцию I(x) если известна аппаратная функция f(x). Рассм. вид апп. функции различных спектральных приборов в предположении, что аберрации отсутствуют и спектральная плотность излучения I(x) и, регистрируемый спектральным прибором некоторый спектр F(х) – пунктирная линия, представляющий свертку I(x) и f(x). входная щель является бесконечно узкой. В призменном спектрографе изображение щели увелич. в связи с тем, что пучок, который падает на призму, пространственно ограничен. Уширение возникает, как и в случае дифракции Фраунгофера на оправе линзы или на краях призмы. Если ширина пучка, падающего на призму равна a, то функция распределения интенсивности: - это позволяет находить функцию I(x) если известна аппаратная функция f(x). Рассм. вид апп. функции различных спектральных приборов в предположении, что аберрации отсутствуют и спектральная плотность излучения I(x) и, регистрируемый спектральным прибором некоторый спектр F(х) – пунктирная линия, представляющий свертку I(x) и f(x). входная щель является бесконечно узкой. В призменном спектрографе изображение щели увелич. в связи с тем, что пучок, который падает на призму, пространственно ограничен. Уширение возникает, как и в случае дифракции Фраунгофера на оправе линзы или на краях призмы. Если ширина пучка, падающего на призму равна a, то функция распределения интенсивности: 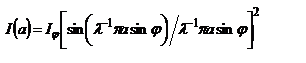 Для дифракционной решетки с N щелями вместо a необходимо подставить Для дифракционной решетки с N щелями вместо a необходимо подставить  , где l — ширина решетки. Угловая и линейная дисперсия. Количественная мера: , где l — ширина решетки. Угловая и линейная дисперсия. Количественная мера:  где где  — изменение угла дисперсии при изменении длины волны света — изменение угла дисперсии при изменении длины волны света  на величину на величину  . С угловой дисперсией связано понятие линейной дисперсии . С угловой дисперсией связано понятие линейной дисперсии  , где dl— , где dl—
расстояние между центрами монохроматических изображений щели для спектральных линий, отстоящих на интервал длин волн  . Угловая дисперсия решетки. В случае дифракционной решетки из условия главных максимумов следует, что . Угловая дисперсия решетки. В случае дифракционной решетки из условия главных максимумов следует, что  , тогда угловая дисперсия , тогда угловая дисперсия  Поскольку решетки, как правило, используются в первых порядках, то углы дифракции являются малыми и можно приближенно считать, что угловая дисперсия является постоянной. Угловая дисперсия призмы. В случае призмы спектральное разложение является результатом дисперсии вещества, из которого она изготовлена. При работе призмы обычно устанавливаются на угол наименьшего отклонения Поскольку решетки, как правило, используются в первых порядках, то углы дифракции являются малыми и можно приближенно считать, что угловая дисперсия является постоянной. Угловая дисперсия призмы. В случае призмы спектральное разложение является результатом дисперсии вещества, из которого она изготовлена. При работе призмы обычно устанавливаются на угол наименьшего отклонения  . Тогда преломляющий угол А, показатель преломления материала n, из которого изготовлена призма и . Тогда преломляющий угол А, показатель преломления материала n, из которого изготовлена призма и  связаны соотношением связаны соотношением  . .
При использовании немонохроматического света показатель преломления вследствие изменения длины волны будет изменяться. Это приведет к соответствующему изменению угла наименьшего отклонения . 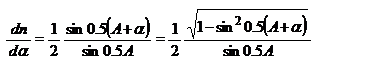 преобразуем: преобразуем:  , В случае призмы угловая дисперсия будет связана с изменением , поэтому выражение для дисперсии представим в виде , В случае призмы угловая дисперсия будет связана с изменением , поэтому выражение для дисперсии представим в виде  , где , где 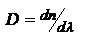 - дисперсия материала. Т.е. угловая дисперсия призмы определяется ее преломляющим углом и дисперсией материала, из которого она изготовлена. Поскольку дисперсия вещества зависит от длины волны света, то и угловая дисперсия призмы также изменяется в зависимости от дины волны проходящего через нее света: наибольшие значения она имеет для синей области видимого спектра и значительно уменьшается в красной области. Разрешающая способность спектрального прибора. С понятием аппаратной функции связана разрешающая способность спектрального прибора, являющаяся его основной характеристикой. Количественно разрешающая способность определяется отношением - дисперсия материала. Т.е. угловая дисперсия призмы определяется ее преломляющим углом и дисперсией материала, из которого она изготовлена. Поскольку дисперсия вещества зависит от длины волны света, то и угловая дисперсия призмы также изменяется в зависимости от дины волны проходящего через нее света: наибольшие значения она имеет для синей области видимого спектра и значительно уменьшается в красной области. Разрешающая способность спектрального прибора. С понятием аппаратной функции связана разрешающая способность спектрального прибора, являющаяся его основной характеристикой. Количественно разрешающая способность определяется отношением 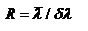 , где , где  - минимальная разность длин волн двух близких спектральных линий с длинами волн - минимальная разность длин волн двух близких спектральных линий с длинами волн  наблюдаются при использовании данного спектрального прибора раздельно, наблюдаются при использовании данного спектрального прибора раздельно, 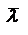 - среднее значение длины волны. С помощью аппаратной функции критерий разрешения может быть определен следующим образом: две спектральные линии будут разрешены (раздельно наблюдаемыми), если расстояние между ними не меньше ширины аппаратной функции на половине высоты ее контура. Разрешающая способность дифракционной решетки. Итак, согласно критерию Рэлея две спектральные линии одинаковой интенсивности будут наблюдаться на пределе разрешения, если главный дифракционный максимум одной из них совпадает с ближайшим к нему минимумом для другой. Запишем условие главного максимума для спектральной линии длиной волны - среднее значение длины волны. С помощью аппаратной функции критерий разрешения может быть определен следующим образом: две спектральные линии будут разрешены (раздельно наблюдаемыми), если расстояние между ними не меньше ширины аппаратной функции на половине высоты ее контура. Разрешающая способность дифракционной решетки. Итак, согласно критерию Рэлея две спектральные линии одинаковой интенсивности будут наблюдаться на пределе разрешения, если главный дифракционный максимум одной из них совпадает с ближайшим к нему минимумом для другой. Запишем условие главного максимума для спектральной линии длиной волны  : :  и условие ближайшего дополнительного минимума для линии l, наблюдаемого в том же порядке дифракции: и условие ближайшего дополнительного минимума для линии l, наблюдаемого в том же порядке дифракции:  . Откуда получаем выражение для разрешающей способности решетки . Откуда получаем выражение для разрешающей способности решетки  . Таким образом, разрешающая способность решетки выше в более высоких порядках. При заданной ширине решетки L=Nd предельная разрешающая способность будет зависеть лишь от размеров решетки. Докажем. Поскольку максимальный порядок дифракции определяется условием, . Таким образом, разрешающая способность решетки выше в более высоких порядках. При заданной ширине решетки L=Nd предельная разрешающая способность будет зависеть лишь от размеров решетки. Докажем. Поскольку максимальный порядок дифракции определяется условием,  , то , то  . Таким образом, при нормальном падении на решетку величина max разрешающей способности не превышает отношения ее размеров к длине волны. Разрешающая способность призмы. Для определения . Таким образом, при нормальном падении на решетку величина max разрешающей способности не превышает отношения ее размеров к длине волны. Разрешающая способность призмы. Для определения 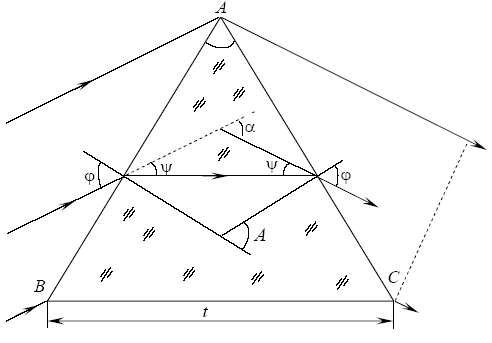 разрешающей способности призмы можно снова воспользоваться критерием Рэлея, в соответствии с которым две близкие спектральные линии с длиной волны разрешающей способности призмы можно снова воспользоваться критерием Рэлея, в соответствии с которым две близкие спектральные линии с длиной волны  и и  будут наблюдаться раздельно, если полуширина дифракционного максимума каждой из линий не больше углового расстояния будут наблюдаться раздельно, если полуширина дифракционного максимума каждой из линий не больше углового расстояния  между ними. Полуширина центрального дифр. Max равна углу между ними. Полуширина центрального дифр. Max равна углу 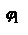 , под которым наблюдается первый фраунгоферов min. Поэтому условием разрешения спектральных линий будет соотношение Рассматривая дифракцию падающего пучка на сечении призмы, имеем: , под которым наблюдается первый фраунгоферов min. Поэтому условием разрешения спектральных линий будет соотношение Рассматривая дифракцию падающего пучка на сечении призмы, имеем:  , где b - min ширина пучка. Изл. спектральных линий , где b - min ширина пучка. Изл. спектральных линий  и и 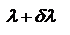 после прохожд. через призму будет разделено на угол, который можно определить, используя угловую дисперсию после прохожд. через призму будет разделено на угол, который можно определить, используя угловую дисперсию  или или  , ,  . Сечение . Сечение  где t=BC – ширина основания призмы. После преобразований: где t=BC – ширина основания призмы. После преобразований:  - показывает, что разрешающая способность призмы определяется размером основания t и дисперсией материала, из которого она изготовлена. Область свободной дисперсии дифракционной решетки и призмы. Область свободной дисперсии спектрального прибора – максимальная разность длин волн спектральных линий, которые будут наблюдаться без наложения в соседних порядках. Область дисперсии и порядок интерференции связаны соотношением - показывает, что разрешающая способность призмы определяется размером основания t и дисперсией материала, из которого она изготовлена. Область свободной дисперсии дифракционной решетки и призмы. Область свободной дисперсии спектрального прибора – максимальная разность длин волн спектральных линий, которые будут наблюдаться без наложения в соседних порядках. Область дисперсии и порядок интерференции связаны соотношением  .В случае дифракционной решетки m будет означать порядок дифракции. Поскольку дифракционные решетки используются в низких порядках дифракции, то область дисперсии для них является достаточно широкой. В первом порядке (m=1) область дисперсии составляет весь видимый диапазон. Это означает, что, будучи разложенным в спектр, излучение всего видимого диапазона в первом порядке наблюдается без наложения со спектром второго порядка. Поскольку при разложении света призмой используется только нулевой (Фраунгоферов) максимум, то область дисперсии призмы ограничена только областью прозрачности материала, из которого она изготовлена. .В случае дифракционной решетки m будет означать порядок дифракции. Поскольку дифракционные решетки используются в низких порядках дифракции, то область дисперсии для них является достаточно широкой. В первом порядке (m=1) область дисперсии составляет весь видимый диапазон. Это означает, что, будучи разложенным в спектр, излучение всего видимого диапазона в первом порядке наблюдается без наложения со спектром второго порядка. Поскольку при разложении света призмой используется только нулевой (Фраунгоферов) максимум, то область дисперсии призмы ограничена только областью прозрачности материала, из которого она изготовлена.
 3,11.Основные принципы голографии. Голографирование плоской и сферической волны. Принципиальная схема двухлучевой голографии. Получение цветных объемных голограмм. Особенности голограмм как носителей информации. Применение голограмм. Голографией (от греческого, holos – полный + graphe – запись) называется метод регистрации изображений, который дает возможность записывать на некоторый носитель (фотопластинки и другие светочувствительные устройства) полную информацию о падающей волне, включающую амплитуду, фазу, длину волны и направление распространения. Процесс получения изображения по имеющейся голограмме называется восстановлением голограммы. Идея голографии была впервые высказана Габором (1947 – 1948 гг..). Голографирование плоской волны: Пусть на фотопластинку падает плоская волна 3,11.Основные принципы голографии. Голографирование плоской и сферической волны. Принципиальная схема двухлучевой голографии. Получение цветных объемных голограмм. Особенности голограмм как носителей информации. Применение голограмм. Голографией (от греческого, holos – полный + graphe – запись) называется метод регистрации изображений, который дает возможность записывать на некоторый носитель (фотопластинки и другие светочувствительные устройства) полную информацию о падающей волне, включающую амплитуду, фазу, длину волны и направление распространения. Процесс получения изображения по имеющейся голограмме называется восстановлением голограммы. Идея голографии была впервые высказана Габором (1947 – 1948 гг..). Голографирование плоской волны: Пусть на фотопластинку падает плоская волна

 Будем называть ее предметной или сигнальной. Будем называть ее предметной или сигнальной.
- Опорная волна

В соответствии с принципом суперпозиции при малых
 Голографирование сферической волны. Голографирование сферической волны.
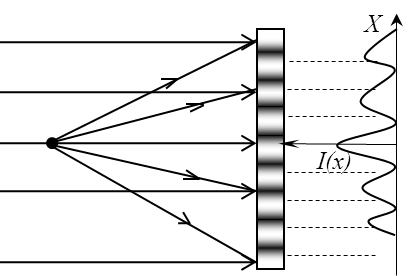
Рассмотрим интерференцию когерентных плоской и сферической волн. Интенсивность в некоторой точке будет также определяться разностью хода интерферирующих волн:  . .
Интерференционная картина будет иметь вид концентрических колец, причём радиус m-го светового кольца определяется аналогично формуле для колец Ньютона:  , где m=0,1,2,…, R-радиус кривизны волнового фронта, или расстояние от фотопластинки до точечного источника. Цветное объемное изображение. Хорошо известно, что любой цвет может быть представлен как смесь трех независимых цветов, в качестве которых обычно можно взять, на пример, красный, зеленый, синий. Цветное изображение получается в результате совмещения изображений в трех цветах. , где m=0,1,2,…, R-радиус кривизны волнового фронта, или расстояние от фотопластинки до точечного источника. Цветное объемное изображение. Хорошо известно, что любой цвет может быть представлен как смесь трех независимых цветов, в качестве которых обычно можно взять, на пример, красный, зеленый, синий. Цветное изображение получается в результате совмещения изображений в трех цветах.
Применения голографии. Первоначальная задача голографии заключалась в получении объемного изображения. С развитием голографии на толстослойных пластинках возникла возможность создания объемных цветных фотографий. На этой базе исследуются пути реализации голографического кино, телевидения и т. д. Из технологических применений наиболее значительно разработана голографическая интерферометрия. Восстановленная по голограмме волна дает копию объекта в тот момент времени, когда записывалась голограмма. Если эту волну сравнить с волной от объекта, восстановленной по голограмме и записанной в другой момент времени, то можно сделать заключение об изменениях в объекте за время между моментами записи голограмм. Поскольку голограмма фиксирует предмет с очень большой точностью, такой метод позволяет изучать с большой точностью явления, которые влияют на голограмму, например деформации, колебания и т. д. Метод называется голографической интерферометрией. Голограммы также могут эффективно использоваться для решения различных задач, связанных с распознаванием образов. По своему физическому содержанию решение этой задачи сводится к осуществлению пространственной фильтрации изображений.
4.1. Геометрическая оптика как предельный случай волновой. Геометрическая оптика представляет собой предельный случай волновой оптики, при котором длина световой волны является малой величиной по сравнению с характерными размерами элементов оптических систем. Длины световых волн, очень малы. Поэтому распространение света во многих случаях можно рассматривать отвлекаясь от его волновой природы, и считать, что свет распространяется вдоль лучей. В пределе  , а также когда угол расходимости , а также когда угол расходимости  законы можно сформулировать на языке геометрии. Законы: 1. з-н прямолинейного распространения света в однородной среде. 2. з-н отражения света: угол отражения равен углу падения. 3. з-н преломления: законы можно сформулировать на языке геометрии. Законы: 1. з-н прямолинейного распространения света в однородной среде. 2. з-н отражения света: угол отражения равен углу падения. 3. з-н преломления:  . Если свет падает на менее плотную опт. среду, угол преломления может достичь . Если свет падает на менее плотную опт. среду, угол преломления может достичь  тогда соответствующий угол падения называют предельным: тогда соответствующий угол падения называют предельным:  . Для углов падения . Для углов падения  наблюдается полное внутреннее отражение. Принцип Ферма: свет распространяется по такому пути, время прохождения которого было бы минимальным, а точнее экстремальным, т.е. либо минимальным либо максимальным, либо стационарным, т.е. для разных путей одинаковое время прохождения (например, в линзе). Если среда однородна, то наблюдается полное внутреннее отражение. Принцип Ферма: свет распространяется по такому пути, время прохождения которого было бы минимальным, а точнее экстремальным, т.е. либо минимальным либо максимальным, либо стационарным, т.е. для разных путей одинаковое время прохождения (например, в линзе). Если среда однородна, то  - оптический путь, где - оптический путь, где  - геометрический. Ур-ие эйконала: - геометрический. Ур-ие эйконала:  или или  , где , где  - некоторая скалярная функция координат (эйконал). Основные законы и понятия геометрической оптики: Основу геометрической оптики составляют четыре закона: закон прямолинейного распространения света, независимого распространения световых пучков, отражения и преломления.По закону прямолинейного распространения свет между двумя точками в однородной среде распространяется по прямой, соединяющей эти точки.Световые пучки при пересечении или наложении не влияют друг на друга. Это утверждение составляет закон независимости световых пучков. В соответствии с законом отражения, луч падающий, отраженный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем угол падения равен углу отражения: j=j¢. В соответствии с законом преломления, луч падающий, преломленный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления равно отношению абсолютного показателя преломления второй среды к показателю преломления первой среды - некоторая скалярная функция координат (эйконал). Основные законы и понятия геометрической оптики: Основу геометрической оптики составляют четыре закона: закон прямолинейного распространения света, независимого распространения световых пучков, отражения и преломления.По закону прямолинейного распространения свет между двумя точками в однородной среде распространяется по прямой, соединяющей эти точки.Световые пучки при пересечении или наложении не влияют друг на друга. Это утверждение составляет закон независимости световых пучков. В соответствии с законом отражения, луч падающий, отраженный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем угол падения равен углу отражения: j=j¢. В соответствии с законом преломления, луч падающий, преломленный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления равно отношению абсолютного показателя преломления второй среды к показателю преломления первой среды  где где  . Если лучи исходят из одной точки, то такой пучок называют гомоцентрическим, т.е. имеющим общий центр . Если лучи исходят из одной точки, то такой пучок называют гомоцентрическим, т.е. имеющим общий центр 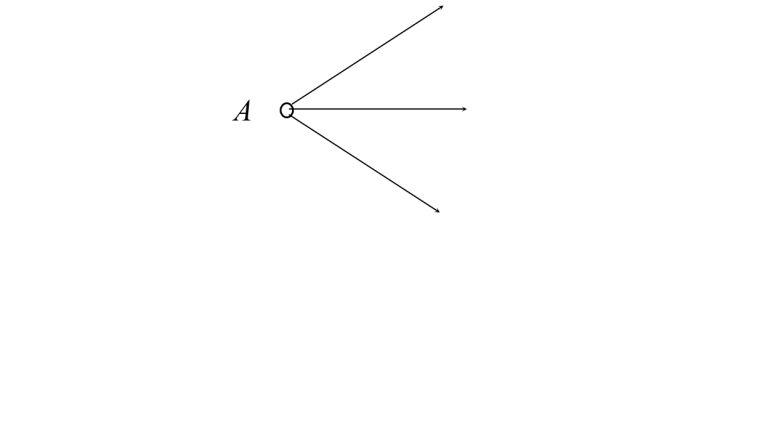
|



 (если апертура больше длины волны). размер дифракционной картины тем меньше, чем больше диметр отверстия D. подавляющая часть светового потока попадает в область центрального светлого пятна – диск Эйри. Пусть плоская волна падает на круглое отверстие радиусом ρ.Дифракция света на круглом отверстии. Координатные оси в области источников и в области дифракции:
(если апертура больше длины волны). размер дифракционной картины тем меньше, чем больше диметр отверстия D. подавляющая часть светового потока попадает в область центрального светлого пятна – диск Эйри. Пусть плоская волна падает на круглое отверстие радиусом ρ.Дифракция света на круглом отверстии. Координатные оси в области источников и в области дифракции: 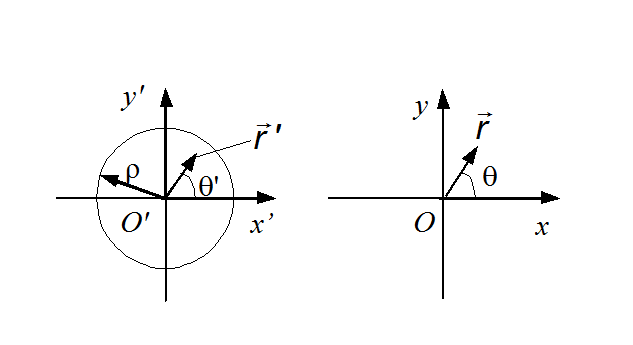
 ,следует, что
,следует, что 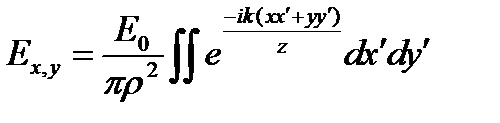 . В полярной системе координат
. В полярной системе координат 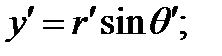
 ,
, 
 ,
,  , следовательно:
, следовательно: . Второй интеграл равен
. Второй интеграл равен 
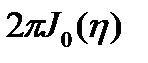 , где
, где  - функция Бесселя нулевого порядка
- функция Бесселя нулевого порядка  Тогда
Тогда  Из теории функций Бесселя:
Из теории функций Бесселя:  где
где  — функция Бесселя первого порядка. Поэтому
— функция Бесселя первого порядка. Поэтому  и
и  . Радиус 1-го тёмного кольца определяется из условия:
. Радиус 1-го тёмного кольца определяется из условия: 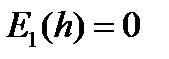 . Угол, под которым это кольцо видно из центра круглого отверстия:
. Угол, под которым это кольцо видно из центра круглого отверстия: 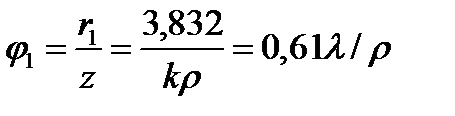 . Угловой размер светлого пятна:
. Угловой размер светлого пятна:  . Второе и третье тёмное пятно наблюдаются под углами:
. Второе и третье тёмное пятно наблюдаются под углами: 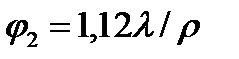 и
и  .
. Разность хода: ΔL =dsinφ, Сдвиг фаз:
Разность хода: ΔL =dsinφ, Сдвиг фаз:  . Амплитуда волны создаваемой щелью вследствие дифракции:
. Амплитуда волны создаваемой щелью вследствие дифракции:  , где
, где 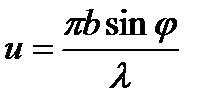 . Фазу волны, создаваемой первой щелью положим равной нулю. Тогда её амплитуда будет равна:
. Фазу волны, создаваемой первой щелью положим равной нулю. Тогда её амплитуда будет равна: . Комплексные амплитуды, волн создаваемых последующими щелями, будут равны:
. Комплексные амплитуды, волн создаваемых последующими щелями, будут равны:  ,
, 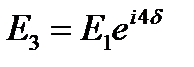 , ………………….,
, ………………….,  . Амплитуда результирующего поля:
. Амплитуда результирующего поля:  ,
,  . Амплитуда результирующей волны:
. Амплитуда результирующей волны:  . Интенсивность результирующей волны:
. Интенсивность результирующей волны:  ,
,  - характеризует распределение интенсивности при дифракции света на каждой из щелей.
- характеризует распределение интенсивности при дифракции света на каждой из щелей.  - учитывает взаимную интерференцию волн, создаваемых N щелями. Условия интерференционных максимумов: dsinφ=mλ (4). Выражение (4) называется условием главных максимумовпри дифракции на решётке. Числа m=0,
- учитывает взаимную интерференцию волн, создаваемых N щелями. Условия интерференционных максимумов: dsinφ=mλ (4). Выражение (4) называется условием главных максимумовпри дифракции на решётке. Числа m=0,  1,
1,  2,… определяют порядок дифракционных максимумов. При j=0 и m =0 следует, что I(0) = N2 I0. Условие минимумов. Минимумы при дифракции на решётке из N щелей: bsin j =m ¢l. (5) Полученные минимумы называются прежними минимумами, Условие (5) называется условием прежних минимумов.Условия дополнительных минимумов:
2,… определяют порядок дифракционных максимумов. При j=0 и m =0 следует, что I(0) = N2 I0. Условие минимумов. Минимумы при дифракции на решётке из N щелей: bsin j =m ¢l. (5) Полученные минимумы называются прежними минимумами, Условие (5) называется условием прежних минимумов.Условия дополнительных минимумов: 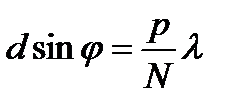 , где p= 1, 2,..., N -1, N+ 1,.... p =0 и p=N, p=2N,... образуют главные максимумы, поэтому они исключаются из условия дополнительных минимумов. bsinj=m ¢ ¢ l, где
, где p= 1, 2,..., N -1, N+ 1,.... p =0 и p=N, p=2N,... образуют главные максимумы, поэтому они исключаются из условия дополнительных минимумов. bsinj=m ¢ ¢ l, где  . Условия дополнительных минимумов:
. Условия дополнительных минимумов: 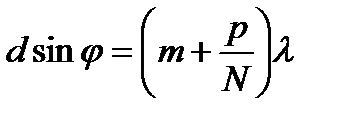 , где P= 1,2,3,... N -1. P – номер дополнительного дифракционного минимума, отсчитанного от ближайшего слева максимума.Наклонное падение плоской волны на решётку: Разность хода волн, дифрагирующих под углом φ: Δ=d* *
, где P= 1,2,3,... N -1. P – номер дополнительного дифракционного минимума, отсчитанного от ближайшего слева максимума.Наклонное падение плоской волны на решётку: Разность хода волн, дифрагирующих под углом φ: Δ=d* *  , где Θ – угол падения волны на решётку. Условие главных максимумов:
, где Θ – угол падения волны на решётку. Условие главных максимумов: 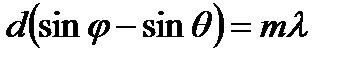 или
или 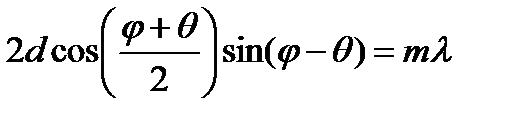 (10), где
(10), где 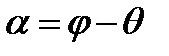 - угол отклонения лучей от первоначального направления. Выражение (10) можно представить в виде:
- угол отклонения лучей от первоначального направления. Выражение (10) можно представить в виде:  , где
, где  и
и  . Если угол падения Θ является большим (Θ →
. Если угол падения Θ является большим (Θ → 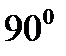 ), то d¢ <<d.
), то d¢ <<d. Фазовая решетка, работающая на пропускании (а) и отражении (б) света. Решётки, принцип действия которых основан на измерении фазы, называются фазовыми решётками. Примером фазовой решётки является отражательная решётка с профилированным штрихом.
Фазовая решетка, работающая на пропускании (а) и отражении (б) света. Решётки, принцип действия которых основан на измерении фазы, называются фазовыми решётками. Примером фазовой решётки является отражательная решётка с профилированным штрихом.  Разность хода:
Разность хода:  , где q - угол падения, j - угол дифракции. Угол падения света на плоскость штриха будет равен
, где q - угол падения, j - угол дифракции. Угол падения света на плоскость штриха будет равен  , угол отражения -
, угол отражения -  . Тогда
. Тогда  , откуда
, откуда  , следовательно
, следовательно  . Главные максимумы:
. Главные максимумы:  или
или  . Порядок дифракционного спектра:
. Порядок дифракционного спектра:  или
или  ,где h – высота профиля штриха. Если, например
,где h – высота профиля штриха. Если, например  , то для решётки будет второй дифракционный максимум. Распределение интенсивности сдвинется относительно распределения
, то для решётки будет второй дифракционный максимум. Распределение интенсивности сдвинется относительно распределения  , для которого главный максимум наблюдается при
, для которого главный максимум наблюдается при  . Синусоидальная решётка Релея. Рассмотрим прохождение плоской волны E0 через периодическую структуру, коэффициент пропускания которой характеризуется гармонической функцией:
. Синусоидальная решётка Релея. Рассмотрим прохождение плоской волны E0 через периодическую структуру, коэффициент пропускания которой характеризуется гармонической функцией:  где 0< р <1, g≤0,5. Вид функции пропускания для решетки со штрихами (а) и синусоидальной решетки Рэлея:
где 0< р <1, g≤0,5. Вид функции пропускания для решетки со штрихами (а) и синусоидальной решетки Рэлея: Поле за решёткой будет иметь вид:
Поле за решёткой будет иметь вид:  ,
, . Определим поле создаваемое одним (первым) периодом:
. Определим поле создаваемое одним (первым) периодом:  . Поскольку
. Поскольку  , то
, то 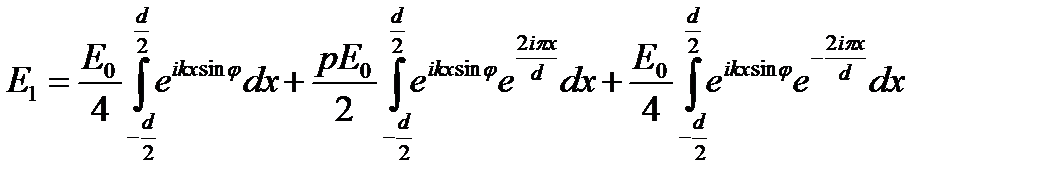 ,
,  . Интенсивность, создаваемая всей решёткой, имеющей N периодов:
. Интенсивность, создаваемая всей решёткой, имеющей N периодов: 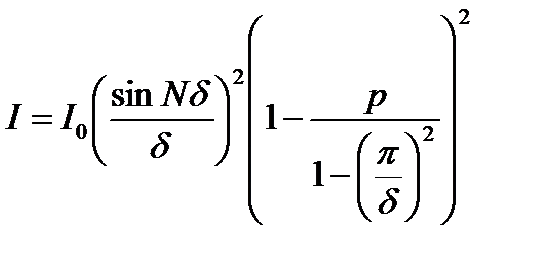 (16). При
(16). При  имеем sinN d=0. При m =0, m =1 и m =-1 при раскрытии неопределённости в (16) получаются максимумы интенсивности. Решётка Релея даёт только три максимума: нулевой при m=0 и два максимума в первых порядках при m =±1.
имеем sinN d=0. При m =0, m =1 и m =-1 при раскрытии неопределённости в (16) получаются максимумы интенсивности. Решётка Релея даёт только три максимума: нулевой при m=0 и два максимума в первых порядках при m =±1. который не вносит искажения в распр. энергии спектральной линии, попадающей на входную щель. Реальные приборы вносят изменения и приводят к уширению спектральных линий. Основные причины— дифракция света на вх. щели, которая имеет конечную ширину, аберрации опт. элементов прибора, влияние с-мы регистрации. Совокупное действие спектрального прибора характеризуется аппаратной функцией
который не вносит искажения в распр. энергии спектральной линии, попадающей на входную щель. Реальные приборы вносят изменения и приводят к уширению спектральных линий. Основные причины— дифракция света на вх. щели, которая имеет конечную ширину, аберрации опт. элементов прибора, влияние с-мы регистрации. Совокупное действие спектрального прибора характеризуется аппаратной функцией  . Аппаратная функция представляет отклик прибора на
. Аппаратная функция представляет отклик прибора на  узкий монохром. импульс. Если направить на вход спектрального прибора монохром. излучение, то регистрируемая линия и будет аппаратной функцией. Чем более узкая инструментальная функция, тем меньше искажений вносит прибор. Аппаратная функция искажает регистрируемый спектр. Пусть спектральная плотность излучения задается функцией
узкий монохром. импульс. Если направить на вход спектрального прибора монохром. излучение, то регистрируемая линия и будет аппаратной функцией. Чем более узкая инструментальная функция, тем меньше искажений вносит прибор. Аппаратная функция искажает регистрируемый спектр. Пусть спектральная плотность излучения задается функцией  . После прохожд. через спектральный прибор каждой длине волны соответствует опр. координата на его фокальной плоскости. Поэтому функции
. После прохожд. через спектральный прибор каждой длине волны соответствует опр. координата на его фокальной плоскости. Поэтому функции  . Найдем распр. F(x), которое зарегистрирует спектральный прибор, имеющий аппаратную функцию f(x). Выделим в спектре
. Найдем распр. F(x), которое зарегистрирует спектральный прибор, имеющий аппаратную функцию f(x). Выделим в спектре  представлена заштрихованным прямоугольником Его ширина dx очень малая. Прибор с апп. функцией
представлена заштрихованным прямоугольником Его ширина dx очень малая. Прибор с апп. функцией 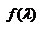 размазывает этот участок в распределение
размазывает этот участок в распределение  ,
,  . Определим значение наблюдаемого распределения F(х') в точке х'. Доля монохром. компоненты, попавшая в точку х', за счет «размазывания» равна произведению апп. функции в этой точке на величину интенсивности линии в этой точке
. Определим значение наблюдаемого распределения F(х') в точке х'. Доля монохром. компоненты, попавшая в точку х', за счет «размазывания» равна произведению апп. функции в этой точке на величину интенсивности линии в этой точке  . Другие монохром. компоненты также дадут вклад в наблюдаемое значение функции в точке x'. В итоге наблюдаемое распр. выразится сверткой функции f(x) и I(x):
. Другие монохром. компоненты также дадут вклад в наблюдаемое значение функции в точке x'. В итоге наблюдаемое распр. выразится сверткой функции f(x) и I(x):  - это позволяет находить функцию I(x) если известна аппаратная функция f(x). Рассм. вид апп. функции различных спектральных приборов в предположении, что аберрации отсутствуют и спектральная плотность излучения I(x) и, регистрируемый спектральным прибором некоторый спектр F(х) – пунктирная линия, представляющий свертку I(x) и f(x). входная щель является бесконечно узкой. В призменном спектрографе изображение щели увелич. в связи с тем, что пучок, который падает на призму, пространственно ограничен. Уширение возникает, как и в случае дифракции Фраунгофера на оправе линзы или на краях призмы. Если ширина пучка, падающего на призму равна a, то функция распределения интенсивности:
- это позволяет находить функцию I(x) если известна аппаратная функция f(x). Рассм. вид апп. функции различных спектральных приборов в предположении, что аберрации отсутствуют и спектральная плотность излучения I(x) и, регистрируемый спектральным прибором некоторый спектр F(х) – пунктирная линия, представляющий свертку I(x) и f(x). входная щель является бесконечно узкой. В призменном спектрографе изображение щели увелич. в связи с тем, что пучок, который падает на призму, пространственно ограничен. Уширение возникает, как и в случае дифракции Фраунгофера на оправе линзы или на краях призмы. Если ширина пучка, падающего на призму равна a, то функция распределения интенсивности: 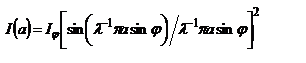 Для дифракционной решетки с N щелями вместо a необходимо подставить
Для дифракционной решетки с N щелями вместо a необходимо подставить  , где l — ширина решетки. Угловая и линейная дисперсия. Количественная мера:
, где l — ширина решетки. Угловая и линейная дисперсия. Количественная мера:  где
где  — изменение угла дисперсии при изменении длины волны света
— изменение угла дисперсии при изменении длины волны света  на величину
на величину  . С угловой дисперсией связано понятие линейной дисперсии
. С угловой дисперсией связано понятие линейной дисперсии  , где dl—
, где dl— . Угловая дисперсия решетки. В случае дифракционной решетки из условия главных максимумов следует, что
. Угловая дисперсия решетки. В случае дифракционной решетки из условия главных максимумов следует, что  , тогда угловая дисперсия
, тогда угловая дисперсия  Поскольку решетки, как правило, используются в первых порядках, то углы дифракции являются малыми и можно приближенно считать, что угловая дисперсия является постоянной. Угловая дисперсия призмы. В случае призмы спектральное разложение является результатом дисперсии вещества, из которого она изготовлена. При работе призмы обычно устанавливаются на угол наименьшего отклонения
Поскольку решетки, как правило, используются в первых порядках, то углы дифракции являются малыми и можно приближенно считать, что угловая дисперсия является постоянной. Угловая дисперсия призмы. В случае призмы спектральное разложение является результатом дисперсии вещества, из которого она изготовлена. При работе призмы обычно устанавливаются на угол наименьшего отклонения  . Тогда преломляющий угол А, показатель преломления материала n, из которого изготовлена призма и
. Тогда преломляющий угол А, показатель преломления материала n, из которого изготовлена призма и 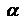 связаны соотношением
связаны соотношением  .
.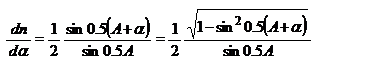 преобразуем:
преобразуем:  , В случае призмы угловая дисперсия будет связана с изменением , поэтому выражение для дисперсии представим в виде
, В случае призмы угловая дисперсия будет связана с изменением , поэтому выражение для дисперсии представим в виде  , где
, где 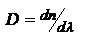 - дисперсия материала. Т.е. угловая дисперсия призмы определяется ее преломляющим углом и дисперсией материала, из которого она изготовлена. Поскольку дисперсия вещества зависит от длины волны света, то и угловая дисперсия призмы также изменяется в зависимости от дины волны проходящего через нее света: наибольшие значения она имеет для синей области видимого спектра и значительно уменьшается в красной области. Разрешающая способность спектрального прибора. С понятием аппаратной функции связана разрешающая способность спектрального прибора, являющаяся его основной характеристикой. Количественно разрешающая способность определяется отношением
- дисперсия материала. Т.е. угловая дисперсия призмы определяется ее преломляющим углом и дисперсией материала, из которого она изготовлена. Поскольку дисперсия вещества зависит от длины волны света, то и угловая дисперсия призмы также изменяется в зависимости от дины волны проходящего через нее света: наибольшие значения она имеет для синей области видимого спектра и значительно уменьшается в красной области. Разрешающая способность спектрального прибора. С понятием аппаратной функции связана разрешающая способность спектрального прибора, являющаяся его основной характеристикой. Количественно разрешающая способность определяется отношением 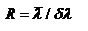 , где
, где  - минимальная разность длин волн двух близких спектральных линий с длинами волн
- минимальная разность длин волн двух близких спектральных линий с длинами волн  наблюдаются при использовании данного спектрального прибора раздельно,
наблюдаются при использовании данного спектрального прибора раздельно, 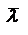 - среднее значение длины волны. С помощью аппаратной функции критерий разрешения может быть определен следующим образом: две спектральные линии будут разрешены (раздельно наблюдаемыми), если расстояние между ними не меньше ширины аппаратной функции на половине высоты ее контура. Разрешающая способность дифракционной решетки. Итак, согласно критерию Рэлея две спектральные линии одинаковой интенсивности будут наблюдаться на пределе разрешения, если главный дифракционный максимум одной из них совпадает с ближайшим к нему минимумом для другой. Запишем условие главного максимума для спектральной линии длиной волны
- среднее значение длины волны. С помощью аппаратной функции критерий разрешения может быть определен следующим образом: две спектральные линии будут разрешены (раздельно наблюдаемыми), если расстояние между ними не меньше ширины аппаратной функции на половине высоты ее контура. Разрешающая способность дифракционной решетки. Итак, согласно критерию Рэлея две спектральные линии одинаковой интенсивности будут наблюдаться на пределе разрешения, если главный дифракционный максимум одной из них совпадает с ближайшим к нему минимумом для другой. Запишем условие главного максимума для спектральной линии длиной волны  :
:  и условие ближайшего дополнительного минимума для линии l, наблюдаемого в том же порядке дифракции:
и условие ближайшего дополнительного минимума для линии l, наблюдаемого в том же порядке дифракции:  . Откуда получаем выражение для разрешающей способности решетки
. Откуда получаем выражение для разрешающей способности решетки  . Таким образом, разрешающая способность решетки выше в более высоких порядках. При заданной ширине решетки L=Nd предельная разрешающая способность будет зависеть лишь от размеров решетки. Докажем. Поскольку максимальный порядок дифракции определяется условием,
. Таким образом, разрешающая способность решетки выше в более высоких порядках. При заданной ширине решетки L=Nd предельная разрешающая способность будет зависеть лишь от размеров решетки. Докажем. Поскольку максимальный порядок дифракции определяется условием,  , то
, то  . Таким образом, при нормальном падении на решетку величина max разрешающей способности не превышает отношения ее размеров к длине волны. Разрешающая способность призмы. Для определения
. Таким образом, при нормальном падении на решетку величина max разрешающей способности не превышает отношения ее размеров к длине волны. Разрешающая способность призмы. Для определения  разрешающей способности призмы можно снова воспользоваться критерием Рэлея, в соответствии с которым две близкие спектральные линии с длиной волны
разрешающей способности призмы можно снова воспользоваться критерием Рэлея, в соответствии с которым две близкие спектральные линии с длиной волны  и
и  будут наблюдаться раздельно, если полуширина дифракционного максимума каждой из линий не больше углового расстояния
будут наблюдаться раздельно, если полуширина дифракционного максимума каждой из линий не больше углового расстояния  между ними. Полуширина центрального дифр. Max равна углу
между ними. Полуширина центрального дифр. Max равна углу 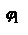 , под которым наблюдается первый фраунгоферов min. Поэтому условием разрешения спектральных линий будет соотношение Рассматривая дифракцию падающего пучка на сечении призмы, имеем:
, под которым наблюдается первый фраунгоферов min. Поэтому условием разрешения спектральных линий будет соотношение Рассматривая дифракцию падающего пучка на сечении призмы, имеем:  , где b - min ширина пучка. Изл. спектральных линий
, где b - min ширина пучка. Изл. спектральных линий  и
и 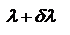 после прохожд. через призму будет разделено на угол, который можно определить, используя угловую дисперсию
после прохожд. через призму будет разделено на угол, который можно определить, используя угловую дисперсию  или
или  ,
,  . Сечение
. Сечение  где t=BC – ширина основания призмы. После преобразований:
где t=BC – ширина основания призмы. После преобразований:  - показывает, что разрешающая способность призмы определяется размером основания t и дисперсией материала, из которого она изготовлена. Область свободной дисперсии дифракционной решетки и призмы. Область свободной дисперсии спектрального прибора – максимальная разность длин волн спектральных линий, которые будут наблюдаться без наложения в соседних порядках. Область дисперсии и порядок интерференции связаны соотношением
- показывает, что разрешающая способность призмы определяется размером основания t и дисперсией материала, из которого она изготовлена. Область свободной дисперсии дифракционной решетки и призмы. Область свободной дисперсии спектрального прибора – максимальная разность длин волн спектральных линий, которые будут наблюдаться без наложения в соседних порядках. Область дисперсии и порядок интерференции связаны соотношением 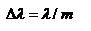 .В случае дифракционной решетки m будет означать порядок дифракции. Поскольку дифракционные решетки используются в низких порядках дифракции, то область дисперсии для них является достаточно широкой. В первом порядке (m=1) область дисперсии составляет весь видимый диапазон. Это означает, что, будучи разложенным в спектр, излучение всего видимого диапазона в первом порядке наблюдается без наложения со спектром второго порядка. Поскольку при разложении света призмой используется только нулевой (Фраунгоферов) максимум, то область дисперсии призмы ограничена только областью прозрачности материала, из которого она изготовлена.
.В случае дифракционной решетки m будет означать порядок дифракции. Поскольку дифракционные решетки используются в низких порядках дифракции, то область дисперсии для них является достаточно широкой. В первом порядке (m=1) область дисперсии составляет весь видимый диапазон. Это означает, что, будучи разложенным в спектр, излучение всего видимого диапазона в первом порядке наблюдается без наложения со спектром второго порядка. Поскольку при разложении света призмой используется только нулевой (Фраунгоферов) максимум, то область дисперсии призмы ограничена только областью прозрачности материала, из которого она изготовлена. 3,11.Основные принципы голографии. Голографирование плоской и сферической волны. Принципиальная схема двухлучевой голографии. Получение цветных объемных голограмм. Особенности голограмм как носителей информации. Применение голограмм. Голографией (от греческого, holos – полный + graphe – запись) называется метод регистрации изображений, который дает возможность записывать на некоторый носитель (фотопластинки и другие светочувствительные устройства) полную информацию о падающей волне, включающую амплитуду, фазу, длину волны и направление распространения. Процесс получения изображения по имеющейся голограмме называется восстановлением голограммы. Идея голографии была впервые высказана Габором (1947 – 1948 гг..). Голографирование плоской волны: Пусть на фотопластинку падает плоская волна
3,11.Основные принципы голографии. Голографирование плоской и сферической волны. Принципиальная схема двухлучевой голографии. Получение цветных объемных голограмм. Особенности голограмм как носителей информации. Применение голограмм. Голографией (от греческого, holos – полный + graphe – запись) называется метод регистрации изображений, который дает возможность записывать на некоторый носитель (фотопластинки и другие светочувствительные устройства) полную информацию о падающей волне, включающую амплитуду, фазу, длину волны и направление распространения. Процесс получения изображения по имеющейся голограмме называется восстановлением голограммы. Идея голографии была впервые высказана Габором (1947 – 1948 гг..). Голографирование плоской волны: Пусть на фотопластинку падает плоская волна
 Будем называть ее предметной или сигнальной.
Будем называть ее предметной или сигнальной.
 Голографирование сферической волны.
Голографирование сферической волны.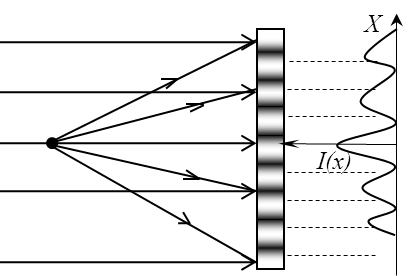
 .
. , где m=0,1,2,…, R-радиус кривизны волнового фронта, или расстояние от фотопластинки до точечного источника. Цветное объемное изображение. Хорошо известно, что любой цвет может быть представлен как смесь трех независимых цветов, в качестве которых обычно можно взять, на пример, красный, зеленый, синий. Цветное изображение получается в результате совмещения изображений в трех цветах.
, где m=0,1,2,…, R-радиус кривизны волнового фронта, или расстояние от фотопластинки до точечного источника. Цветное объемное изображение. Хорошо известно, что любой цвет может быть представлен как смесь трех независимых цветов, в качестве которых обычно можно взять, на пример, красный, зеленый, синий. Цветное изображение получается в результате совмещения изображений в трех цветах. , а также когда угол расходимости
, а также когда угол расходимости  законы можно сформулировать на языке геометрии. Законы: 1. з-н прямолинейного распространения света в однородной среде. 2. з-н отражения света: угол отражения равен углу падения. 3. з-н преломления:
законы можно сформулировать на языке геометрии. Законы: 1. з-н прямолинейного распространения света в однородной среде. 2. з-н отражения света: угол отражения равен углу падения. 3. з-н преломления:  . Если свет падает на менее плотную опт. среду, угол преломления может достичь
. Если свет падает на менее плотную опт. среду, угол преломления может достичь  тогда соответствующий угол падения называют предельным:
тогда соответствующий угол падения называют предельным:  . Для углов падения
. Для углов падения  наблюдается полное внутреннее отражение. Принцип Ферма: свет распространяется по такому пути, время прохождения которого было бы минимальным, а точнее экстремальным, т.е. либо минимальным либо максимальным, либо стационарным, т.е. для разных путей одинаковое время прохождения (например, в линзе). Если среда однородна, то
наблюдается полное внутреннее отражение. Принцип Ферма: свет распространяется по такому пути, время прохождения которого было бы минимальным, а точнее экстремальным, т.е. либо минимальным либо максимальным, либо стационарным, т.е. для разных путей одинаковое время прохождения (например, в линзе). Если среда однородна, то  - оптический путь, где
- оптический путь, где  - геометрический. Ур-ие эйконала:
- геометрический. Ур-ие эйконала:  или
или  , где
, где  - некоторая скалярная функция координат (эйконал). Основные законы и понятия геометрической оптики: Основу геометрической оптики составляют четыре закона: закон прямолинейного распространения света, независимого распространения световых пучков, отражения и преломления.По закону прямолинейного распространения свет между двумя точками в однородной среде распространяется по прямой, соединяющей эти точки.Световые пучки при пересечении или наложении не влияют друг на друга. Это утверждение составляет закон независимости световых пучков. В соответствии с законом отражения, луч падающий, отраженный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем угол падения равен углу отражения: j=j¢. В соответствии с законом преломления, луч падающий, преломленный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления равно отношению абсолютного показателя преломления второй среды к показателю преломления первой среды
- некоторая скалярная функция координат (эйконал). Основные законы и понятия геометрической оптики: Основу геометрической оптики составляют четыре закона: закон прямолинейного распространения света, независимого распространения световых пучков, отражения и преломления.По закону прямолинейного распространения свет между двумя точками в однородной среде распространяется по прямой, соединяющей эти точки.Световые пучки при пересечении или наложении не влияют друг на друга. Это утверждение составляет закон независимости световых пучков. В соответствии с законом отражения, луч падающий, отраженный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем угол падения равен углу отражения: j=j¢. В соответствии с законом преломления, луч падающий, преломленный и нормаль к границе раздела, проведенная в точку падения, лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления равно отношению абсолютного показателя преломления второй среды к показателю преломления первой среды  где
где  . Если лучи исходят из одной точки, то такой пучок называют гомоцентрическим, т.е. имеющим общий центр
. Если лучи исходят из одной точки, то такой пучок называют гомоцентрическим, т.е. имеющим общий центр 



