
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторна робота № 5. 2. Визначення довжини світлової хвилі за допомогою дифракційних ґратСодержание книги
Поиск на нашем сайте
Мета роботи: вивчити явище дифракції; визначити за допомогою дифракційних ґрат довжину світлової хвилі; визначити товщину люд-ської волосини за дифракційною картиною.
Вказівки до виконання роботи Для виконання роботи потрібно засвоїти такий теоретичний матеріал: дифракція хвиль; дифракція в паралельних променях; дифракційні ґрати та їхні характеристики. Література: [ 1, т.3 §§ 4.1–4.5; 2, §§ 176–181; 3, §§ 12.4–12.6; 4, т.2 §§ 125–130].
Перед виконанням ознайомитись з вказівками до роботи № 5.1. Дифракцією називають явища, пов’язані з огинанням хвилями перешкод, які трапляються на їхньому шляху, або, в більш широкому розумінні, явища, пов’язані з будь-яким відхиленням від законів геометричної оптики в процесі поширення світла. Для пояснення явища дифракції Гюйгенс сформулював принцип, згідно з яким кожна точка простору, до якої доходить хвильовий фронт, стає центром вторинних когерентних хвиль, а огинаюча цих хвиль дає положення хвильового фронту в наступний момент часу.
Якщо ширина перешкоди (наприклад, щілина) дорівнює b, відстань від неї до точки спостереження – l, а довжина хвилі – l, то параметр
Дифракційні ґрати – це система паралельних щілин однакової ширини, які лежать в одній площині і розділені однаковими за шириною непрозорими проміжками. Якщо а – ширина непрозорої частини, а b – ширина прозорої щілини, то сума d = b + a має назву сталої (періоду) дифракційної решітки. Якщо кількість прозорих щілин грат на одиниці довжини l буде N (число штрихів), то сталу дифракційних ґрат знаходять за співвід-ношенням: Нехай на дифракційні ґрати падає плоска світлова хвиля (рис. 5.2.1). Згідно з принципом Гюйгенса – Френеля кожна точка цього фронту є джерелом вторинних сферичних когерентних хвиль. Внаслідок цього усі точки кожної щілини випромінюють сферичні хвилі. Візьмемо, наприклад, точки, що лежать біля країв усіх щілин і розглянемо промені, які виходять під кутом
Якщо на цій різниці ходу вкладається ціле число довжини хвиль, виникає інтерференційний максимум. Таким чином, умовою основних дифракційних максимумів є:
де Частина 1 Якщо кути дифракції малі (рис. 5.2.3), то
З виразів (5.2.2) та (5.2.3) випливає, що довжина хвилі:
де
У цій лабораторній роботі джерелом світла є оптичний квантовий генератор ОКГ (лазер). Схему лабораторної установки зображено на рис. 5.2.3. Випромінювання лазера (ОКГ) проходить крізь дифракційні ґрати ДР і створює на екрані Е картину дифракції. Порядок виконання роботи 1. Отримати у лаборанта набір дифракційних грат та згідно з інструкцією ввімкнути лазер. 2. Визначити кількість штрихів N на одиницю довжини для кожних дифракційних ґрат та розрахувати сталу 3. Встановити на шляху лазерного променя дифракційні ґрати з відомою кількістю штрихів 4. Спостерігаючи на екрані картину дифракції, виміряти відстані 5. Виконати операції пп. 2−3 для всіх дифракційних ґрат. 6. Визначити відстань від гратки до екрана 7. Обчислити довжину світлової хвилі за формулою (5.2.4) для кожного вимірювання 8. Обчислити середнє значення довжини хвилі 9. Дані записати в табл. 5.2.1. Таблиця 5.1.1
Частина 2
Випромінювання лазера проходить крізь волосину В й утворює на екрані Е картину дифракції. Формула (5.2.2) для випадку дифракції на одній перешкоді завширшки
З виразів (5.2.2) і (5.2.3) випливає, що
де Записавши вираз (5.2.6) для двох сусідніх максимумів та віднявши одне рівняння від іншого, отримуємо формулу для обчислення товщини волосини:
де
Порядок виконання роботи 1. Волосину закріпити перпендикулярно до пучка променів лазера. 2. Три рази виміряти на екрані величину 3. Дані записати в табл. 5.2.2. Таблиця 5.2.2
Контрольні запитання 1. Що таке дифракція? Сформулюйте принцип Гюйгенса – Френеля. 2. Що таке когерентність, почасова та просторова когерентність? 3. Які хвилі називають монохроматичними? 4. Чим відрізняється дифракція Фраунгофера від дифракції Френеля? 5. Що таке дифракційні ґрати? Назвіть характеристики дифракційних ґрат. 6. Що таке геометрична й оптична різниця ходу променів? Побудуйте хід променів за дифракції Фраунгофера і покажіть різницю ходу променів. 7. Запишіть умови дифракційних максимумів та мінімумів. Поясніть виникнення дифракційного спектра в білому світлі.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 Френель доповнив принцип Гюйгенса ідеєю інтерференції
Френель доповнив принцип Гюйгенса ідеєю інтерференції  . Тоді залежно від кількості зон
. Тоді залежно від кількості зон 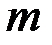 в точці М може спостерігатись посилення або послаблення інтенсивності хвиль в разі їхнього накладання.
в точці М може спостерігатись посилення або послаблення інтенсивності хвиль в разі їхнього накладання. визначає число зон Френеля m, які відкриває ця перешкода. Отже, дифракцію можна спостерігати лише тоді, коли m <<1 (дифракція Фраунгофера), або за m ~ 1 (дифракція Френеля). Якщо m >>1, то справджуються закони
визначає число зон Френеля m, які відкриває ця перешкода. Отже, дифракцію можна спостерігати лише тоді, коли m <<1 (дифракція Фраунгофера), або за m ~ 1 (дифракція Френеля). Якщо m >>1, то справджуються закони  Найбільше практичне значення має дифракція, яку спостерігають в паралельних променях (дифракція Фраунгофера) під час проходження світла через одномірні дифракційні ґрати (рис. 5.2.2).
Найбільше практичне значення має дифракція, яку спостерігають в паралельних променях (дифракція Фраунгофера) під час проходження світла через одномірні дифракційні ґрати (рис. 5.2.2).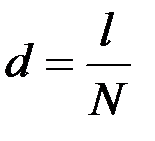 . (5.2.1)
. (5.2.1)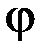 до напряму поширення плоскої хвилі (кути дифракції
до напряму поширення плоскої хвилі (кути дифракції  будемо вважати малими). Освітленість у точці 0 на екрані буде результатом інтерференції усіх променів. З рис. 5.2.1 видно, що між променями 1 та 2 виникає різниця ходу:
будемо вважати малими). Освітленість у точці 0 на екрані буде результатом інтерференції усіх променів. З рис. 5.2.1 видно, що між променями 1 та 2 виникає різниця ходу: .
. , (5.2.2)
, (5.2.2) − стала ґрат;
− стала ґрат; 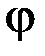 − кут дифракції;
− кут дифракції;  − порядок дифракційного максимуму;
− порядок дифракційного максимуму;  − довжина світлової хвилі.
− довжина світлової хвилі.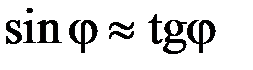 , тобто:
, тобто: . (5.2.3)
. (5.2.3) , (5.2.4)
, (5.2.4)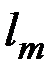 – відстань від центрального максимуму до дифракційного мак-симуму
– відстань від центрального максимуму до дифракційного мак-симуму  -го порядку;
-го порядку;  – відстань від ґрат до екрана.
– відстань від ґрат до екрана. дифракційних ґрат за
дифракційних ґрат за  .
. ,
,  ,
,  від центрального максимуму (
від центрального максимуму (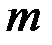 = 0) до максимумів першого, другого і третього порядку (
= 0) до максимумів першого, другого і третього порядку ( = 1, 2, 3).
= 1, 2, 3).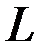 .
.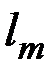 .
. .
. , м
, м
 , мкм
, мкм

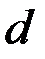 , м
, м
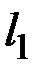 , м
, м
 . Хід променів у цьому випадку показаний на рис. 5.2.3.
. Хід променів у цьому випадку показаний на рис. 5.2.3. (товщина волосини) матиме вигляд:
(товщина волосини) матиме вигляд: . (5.2.5)
. (5.2.5) , (5.2.6)
, (5.2.6)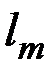 – відстань від центрального максимуму до дифракційного максимуму
– відстань від центрального максимуму до дифракційного максимуму 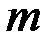 -го порядку.
-го порядку. , (5.2.7)
, (5.2.7)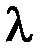 – довжина хвилі випромінювання лазера, значення якої беруть із результатів обчислень, проведених у першій частині роботи;
– довжина хвилі випромінювання лазера, значення якої беруть із результатів обчислень, проведених у першій частині роботи;  – відстань від волосини до екрана;
– відстань від волосини до екрана; 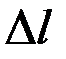 – відстань між двома сусідніми максимумами або мінімумами дифракційної картини
– відстань між двома сусідніми максимумами або мінімумами дифракційної картини  .
.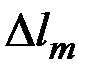 обчислити значення
обчислити значення  за формулою (5.2.7) і знайти середнє значення
за формулою (5.2.7) і знайти середнє значення 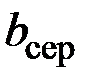 в мікрометрах.
в мікрометрах. , м
, м
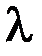 , м
, м
 ,мкм
,мкм
 , м
, м
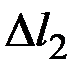 , м
, м
 , м
, м



