
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование явления дифракции ФраунгофераСодержание книги
Поиск на нашем сайте
На дифракционной решётке. Цель работы: Изучение дифракционного спектра, возникающего при дифракции лазерного луча на дифракционной решётке. Определение с помощью дифракционной решётки длины световой волны, разрешающей способности и дисперсии различных дифракционных решеток. Приборы и принадлежности: лазер, набор дифракционных решеток, измерительная линейка, экран. Краткие теоретические сведения. Под дифракцией света понимают любое отклонение от прямолинейного распространения колебаний в среде с резкими неоднородностями (края экранов, отверстия и т.д.), что связано с отклонениями от законов геометрической оптики. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса-Френеля:
1 Каждая точка фронта волны служит центром (источником) вторичных волн, а огибающая этих волн дает положение фронта волны в следующий момент времени (рис.8. 1). 2: Вторичные источники создают когерентные между собой сферические волны. Поэтому новое положение фронта волны, распределение интенсивности света в пространстве — результат интерференции волн от вторичных источников. Рассмотрим дифракцию на дифракционной решётке. Дифракционной решеткой называется совокупность большого числа одинаковых, щелей отстоящих друг от друга на одно и то же расстояние (рис.8.2). Пусть ширина каждой щели равна b, а период решётки (р асстояние между серединами соседних щелей) — d.
D=dsinj. (8.1) Следовательно, разности фаз δ также одинаковы и равны:
Если решётка содержит N щелей, то разность фаз волн, прошедших через последнюю (N) и первую щель будет в N раз больше,
Для тех направлений, для которых разность фаз d=±2p m, т.е. при условии
получим после сокращения на 2p
Формула (8.3) определяет положения максимумов интенсивности, называемых главными, т.к. лучи от отдельных щелей, поскольку их фазы одинаковы, взаимно усиливают друг друга.
Число m дает, так называемый, порядок главного максимума. Максимум нулевого порядка только один, максимумов первого, второго и т.д. по два. Таким образом, дифракционная картина содержит набор дифракционных максимумов (рис.8.3).
люи 4. Характеристики спектрального прибора. Дифракционная решетка разлагает падающий на неё свет в спектр (по длинам волн) т. е. является спектральным прибором. Основными характеристиками любого спектрального прибора являются угловая дисперсия и разрешающая способность. Угловая дисперсия D характеризует степень углового разделения волн с различными l. По определению,
d cosj d j= md l, откуда
Разрешающей способностью R спектрального прибора называют безразмерную величину
где dl – наименьшая разность длин волн двух спектральных линий в окрестности l, при которой эти линии воспринимаются еще раздельно, т.е. разрешаются. Согласно критерию Рэлея, необходимо, чтобы максимум m ‑го порядка линии с длиной волны l+dl совпадал по направлению с первым добавочным минимумом линии l¢ (k ¢= mN +1). Расчёты показывают, что в этом случае
Задание: С помощью дифракционной решётки определить длину световой волны,рассчитать дисперсию и разрешающую способность дифракционных решёток 1. Установить на направляющей необходимые части установки (рис.8.7).
2. С помощью магнитов прикрепить к экрану лист миллиметровой бумаги 3. Дифракционную решетку с известным периодом d — (d=1мм/число щелей приходящихся1 мм) 4. Включить лазер в сеть. 5. Направить луч лазера на дифракционную решетку и, передвигая вдоль скамьи экран, установить его в таком положении, чтобы дифракционная картина занимала бы большую часть экрана, и при этом было бы видно наибольшее количество максимумов. 6. Перерисовать дифракционную картину на миллиметровую бумагу (Центры максимумов обозначить точкой). Отметить центральный максимум.
7. Выключить лазер. Снять бумагу и с возможной максимальной точностью штангенциркулем определить расстояние между центрами симметричных дифракционных максимумов. Результаты измерения занести в таблицу 8.1. 8. Измерить расстояние L от решетки до экрана. Снять миллиметровую бумагу. Измерить расстояния хm (х1, х2,и т.д.) между симметричными максимумами. Все результаты здесь и далее заносить в таблицу с обязательным указанием единиц измерения! 9. Вычислить значения тангенсов углов дифракции. По известным значениям
12. По формулам (8.9) и (8.11) рассчитать угловую дисперсию D и разрешающую способность R дифракционной решетки. 13. Установить вторую и третью дифракционные решётки с другим числом щелей и проделать всё, что указано в пп.3—11. Обратить внимание на характер изменения дифракционной картин.
Определить для одной из решёток погрешность в определении длины волны
Контрольные вопросы 1 Явление дифракции. 2. Принципы Гюйгенса-Френеля. 1. Дифракция Фраунгофера. 2. Условия максимумов и минимумов при дифракции на дифракционной решетке. 3. Объяснение дифракционной картины с помощью векторной диаграммы. 4. Получить условия для получения главных максимумов, для побочных минимумов и побочных максимумов. 5. Вывести формулу для интенсивности побочных максимумов 6. Угловая дисперсия дифракционной решетки. Разрешающая способность дифракционной решетки.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.121.243 (0.011 с.) |

 Рис.8.1. Построение фронта волны.
Рис.8.1. Построение фронта волны.
 На дифракционной решетке осуществляется интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
На дифракционной решетке осуществляется интерференция когерентных дифрагированных пучков света, идущих от всех щелей. 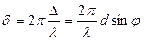 . (8.2)
. (8.2)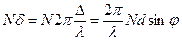
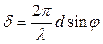 =2p m,
=2p m, d sinj=± m l, m =0, 1, 2, … (8.3)
d sinj=± m l, m =0, 1, 2, … (8.3) Кроме максимумов, определяемых условием (8.3), в промежутках между соседними главными максимумами имеется по (N –1)-му добавочному минимуму (N —число щелей), а между дополнительными минимумами дополнительно появляются слабые вторичные побочные максимумы.
Кроме максимумов, определяемых условием (8.3), в промежутках между соседними главными максимумами имеется по (N –1)-му добавочному минимуму (N —число щелей), а между дополнительными минимумами дополнительно появляются слабые вторичные побочные максимумы.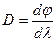 . (8.8)
. (8.8) Взяв дифференциал от соотношения (8.3) при данном m находим:
Взяв дифференциал от соотношения (8.3) при данном m находим: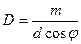 . (8.9)
. (8.9)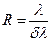 , (8.10)
, (8.10)
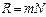 . (8.11)
. (8.11)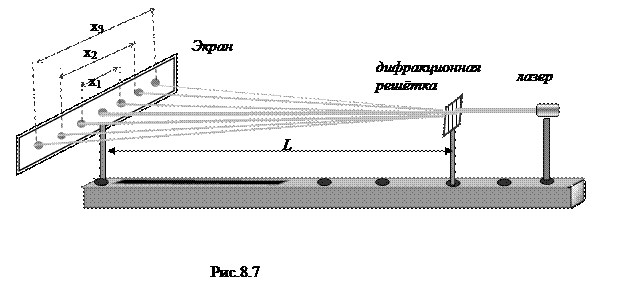
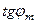 рассчитать значения углов в радианах, а затем и синусов углов, соответствующих измеренным значениям хm.
рассчитать значения углов в радианах, а затем и синусов углов, соответствующих измеренным значениям хm.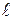 = ….
= ….
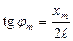
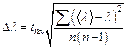 , где tnα— коэффициент Стьюдента для числа измерений n = и надёжности α= 0.95 Записать полученный результат в виде l=<l>±Δl
, где tnα— коэффициент Стьюдента для числа измерений n = и надёжности α= 0.95 Записать полученный результат в виде l=<l>±Δl


