
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция на пространственной решетке. Формула Вульфа-Брэггов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат. Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной. Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:
где φ - угол между направлением на главный максимум (направление луча) и нормалью к решетке; m – порядок дифракционного максимума. Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос. Дифракция наблюдается также и на трехмерных структурах. Всякий монокристалл состоит из упорядоченно расположенных атомов (ионов), образующих пространственную трехмерную решетку (естественная пространственная решетка). Период атомной решетки порядка В 1913 г. русский физик Г.В. Вульф и английские ученые отец и сын Генри и Лоуренс Брэгги, независимо друг от друга, предложили простой метод расчета дифракции рентгеновских лучей в кристаллах. Они полагали, что дифракцию рентгеновских лучей можно рассматривать как результат отражения рентгеновских лучей от плоскостей кристалла. Это отражение, в отличие от обычного, происходит лишь при таких условиях падения лучей на кристалл, которые соответствуют максимуму интерференции для лучей, отраженных от разных плоскостей. Направим пучок рентгеновских лучей 1 и 2 на две соседние плоскости кристалла
Рис. 9.9 Абсолютный показатель преломления всех веществ для рентгеновских лучей равен 1. Поэтому оптическая разность хода между лучами
где θ – угол между падающими и отраженными лучами и плоскостью кристалла (угол скольжения). Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:
Из формулы (9.5.1) видно, что дифракция будет наблюдаться лишь при Из (9.5.1) следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу.
Дисперсия света. Дисперсия света в призме. Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломлениявещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Луч белого света, проходя через трехгранную призму не только отклоняется, но и разлагается на составляющие цветные лучи. Опыты Ньютона Опыт по разложению белого света в спектр:
или
Ньютон направил луч солнечного света через маленькое отверстие на стеклянную призму.
Опыт по прохождению монохроматического света через призму:
Ньютон на пути солнечного луча поставил красное стекло, за которым получил монохроматический свет (красный), далее призму и наблюдал на экране только красное пятно от луча света.
Коэффициент преломления любого материала в той или иной степени зависит от длины волны света. Это свойство, называемое дисперсией, может быть использовано для того, чтобы разложить свет на спектральные составляющие. Одним из устройств, используемых для этих целей, является стеклянная призма.
n = sin (a /2 + j /2) / sin (a /2) (1) На практике коэффициент преломления материала призмы n зависит от длины волны света l, так что угол j, под которым призма преломляет свет, будет также зависеть от длины волны: D = dj / dl = (dj / d n)(d n / dl) (2) Величина d n / dl называется дисперсией материала. Эта константа и коэффициент преломления n (l) характеризуют основные оптические свойства материала, из которого изготовлена призма. Дифференцируя формулу (1), мы можем найти первый сомножитель уравнения (2). Действительно: d n / dj = cos (a /2 + j /2) / 2sin (a /2) (3) и поэтому
Как видно из этой формулы, чтобы достичь максимального спектрального разрешения призмы, мы должны использовать материл с максимальным значением показателя преломления n и дисперсией (d n / dl). Составные цвета в дифракционном и призматическом спектрах располагаются различно. Мы знаем, что синус угла в дифракционной решетке пропорционален длине волны
Рис. 10.3 Поэтому, красные лучи отклоняются призмой слабее, в отличие от дифракционной решетки. Величина
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.157.203 (0.01 с.) |

 и
и  ,
, ; длина волны света
; длина волны света  . При таких условиях никаких дифракционных явлений на атомных дифракционных решетках с видимым светом не будет. Нужно излучение с меньшей длиной волны, например рентгеновское. Для рентгеновских лучей кристаллы твердых тел являются идеальными дифракционными решетками.
. При таких условиях никаких дифракционных явлений на атомных дифракционных решетках с видимым светом не будет. Нужно излучение с меньшей длиной волны, например рентгеновское. Для рентгеновских лучей кристаллы твердых тел являются идеальными дифракционными решетками. и
и 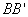 (рис. 9.9).
(рис. 9.9).
 и
и 
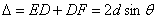 ,
, , (m = 1, 2, 3,....).
, (m = 1, 2, 3,....).
 . Т. е. при условии
. Т. е. при условии  будут отсутствовать дифракционные максимумы. Поэтому условие
будут отсутствовать дифракционные максимумы. Поэтому условие 


 Рассмотрим луч света, распространяющийся симметрично через стеклянную призму (см. рисунок). Еслиa- преломляющий угол призмы, то из формулы Френеля n = sin x0 / sin x =sinz/ sinz0 мы можем найти, что
Рассмотрим луч света, распространяющийся симметрично через стеклянную призму (см. рисунок). Еслиa- преломляющий угол призмы, то из формулы Френеля n = sin x0 / sin x =sinz/ sinz0 мы можем найти, что (4)
(4) . Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи света в спектре по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны (т.е. с уменьшением частоты) уменьшается (рис. 10.3).
. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи света в спектре по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны (т.е. с уменьшением частоты) уменьшается (рис. 10.3).
 (или
(или  ), называемая дисперсией вещества, показывает, как быстро меняется показатель преломления с длиной волны.
), называемая дисперсией вещества, показывает, как быстро меняется показатель преломления с длиной волны.


