
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм расчета сложной электрической цепи постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
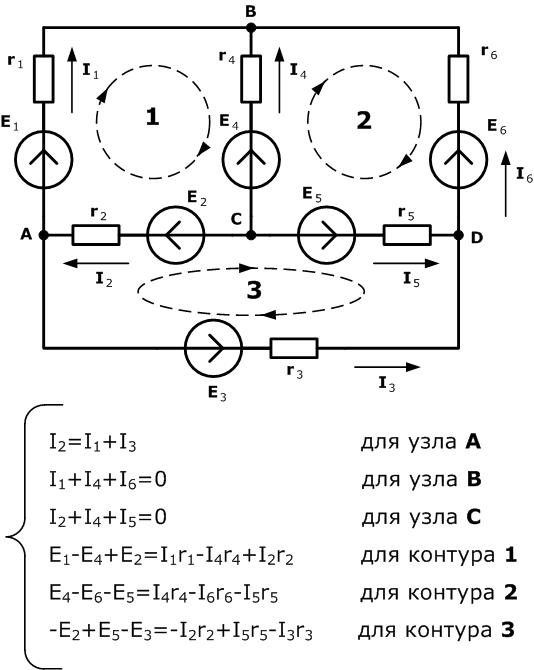
Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системылинейных уравнений c l неизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.) Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными. Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий: 1. Выбирают положительные направления токов в ветвях электрической цепи. 2. Составляют (k -1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество. 3. Выбирают (l - k +1- m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви. 4. Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа. 5. Решают систему из (l - m) линейных уравнений любым удобным способом. Более наглядно методика составления системы уравнений для данного способа расчета сложных электрических цепей показана на рисунке ниже. Для этого выбираем 3 независимых контура электрической цепи и для каждого из них выберем направление обхода. Составляем для каждого выбранного контура уравнение по второму закону Кирхгофа (формула 1.21). Получаем систему из 6 линейных уравнений с 6 неизвестными, которую и решаем любым удобным способом. Магнитное поле. Сила Лоренца. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1]; магнитная составляющая электромагнитного поля[2]. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментамиэлектронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты). Кроме этого, оно возникает в результате изменения во времени электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции Сила Лоренца Сила Ампера, действующая на отрезок проводника длиной Δ l с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда. Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
Так как полное число N носителей свободного заряда в проводнике длиной Δ l и сечением S равно n S Δ l, то сила, действующая на одну заряженную частицу, равна
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью
Сила Лоренца направлена перпендикулярно векторам При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R. Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ. Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
Если скорость частицы
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.01 с.) |

 (вектор индукции магнитного поля)[3][4]. С математической точки зрения
(вектор индукции магнитного поля)[3][4]. С математической точки зрения  —векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).
—векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина). и вектором магнитной индукции
и вектором магнитной индукции 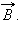 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или поправилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или поправилу буравчика. Взаимное расположение векторов 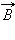 и
и  для положительно заряженной частицы показано на рис. 1.18.1.
для положительно заряженной частицы показано на рис. 1.18.1.
 Модуль силы Лоренца
Модуль силы Лоренца  помноженной на заряд q
помноженной на заряд q





 и
и  и магнитная сила Лоренца. При условии E = υ B эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
и магнитная сила Лоренца. При условии E = υ B эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = m υ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q 1 = q 2) масс-спектрометр позволяет разделить частицы с разными массами.
Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = m υ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q 1 = q 2) масс-спектрометр позволяет разделить частицы с разными массами.
 вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора  а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).




