
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение теоремы Гаусса для расчета симметричных электростатических полей.Содержание книги
Поиск на нашем сайте
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать. Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2π rl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
где τ – заряд единицы длины цилиндра. Отсюда
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити. Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2π rl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю. Потенциал электростатического поля. Теорема о циркуляции электростатического поля в интегральной форме. Теорема о циркуляции электростатического поля в дифференциальной форме. Потенциал уединенного точечного заряда. Разность потенциалов. Эквипотенциальная поверхность. Свойство аддитивности потенциала. Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W п / q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В). Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. Теорема о циркуляции Пусть поле создано системой точечных зарядов. Вычислим интеграл от напряженности по замкнутой траектории.
Данное утверждение и составляет суть теоремы о циркуляции. В математике подобный интеграл называют циркуляцией.
Понятие о циркуляции Пусть в некоторой области пространства существует векторное поле
Здесь Существует соглашение, что положительное направление обхода контура (направление Напомним, вкратце, как можно “сконструировать” криволинейный интеграл. Для этого нужно выбрать точку на контуре, показать в ней вектор Так же, как и поток, циркуляция является ещё одной характеристикой свойств векторного поля. А именно, циркуляция характеризует степень завихренности векторного поля. Пример: если в качестве «измерителя» циркуляции поля скоростей жидкости можно взять турбинку, то если она вращается, циркуляция не равна нулю.
Циркуляция – это интегральная характеристика поля. Понятие ротора Поле по своей структуре может быть достаточно неоднородным. Циркуляция же не дает детальной характеристики поля. Следовательно, начнем стягивать контур интегрирования к какой-либо точке М (уменьшать турбину). Циркуляция при этом будет стремиться к нулю, но и площадь, охваченная контуром, также будет стремиться к нулю. А их отношение дает конечное число.
Турбину можно ориентировать в пространстве тремя независимыми способами. Следовательно, таким способом можно получить 3 независимых числа, а три числа – это вектор, следовательно, образуется векторная характеристика поля, которая и называется ротором.
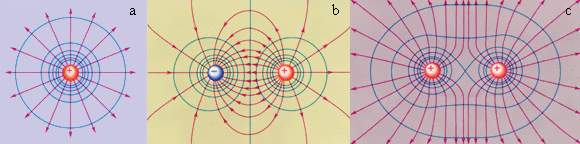
Ротор – это локальная или дифференциальная характеристика. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Если пробный заряд q совершил малое перемещение
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии. Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к модулю этого заряда: Разность потенциалов измеряется в вольтах (В = Дж / Кл) В физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величин, относящихся к её составным частям. Такие величины называются также экстенсивными, в отличие от интенсивных (например, температуры,плотности и т. п.).
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.253.21 (0.009 с.) |








 .
.

 - единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.
- единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.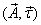 , разбить контур на малые элементы, длину элемента обозначить
, разбить контур на малые элементы, длину элемента обозначить  , вычислить произведение
, вычислить произведение  ; проделать это для всех элементов контура; произвести суммирование результатов, устремляя элемент длины контура
; проделать это для всех элементов контура; произвести суммирование результатов, устремляя элемент длины контура 



 вдоль силовой линии из точки (1) в точку (2), то можно записать:
вдоль силовой линии из точки (1) в точку (2), то можно записать:



