
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические цепи переменного тока. Элементы R, L, C цепей переменного тока. Правила Кирхгофа для цепей переменного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрический ток, возникающий под действием э. д. с, которая изменяется по синусоидальному закону, называют переменным. По существу, переменный ток - это вынужденные колебания тока в электрических цепях.
где
Расчет цепей переменного тока с использованием мгновенных значений тока, напряжения и ЭДС требует громоздкой вычислительной работы. Поэтому изменяющиеся непрерывно во времени токи, напряжения и ЭДС заменяют эквивалентными во времени величинами.
где
где Таким образом, синусоидальное напряжение можно представить на комплексной плоскости вращающимся вектором. Тогда амплитудное значение напряжения Сопротивления в цепи переменного тока Электрический ток в проводниках непрерывно связан с магнитным и электрическими полями. Элементы, характеризующие преобразование электромагнитной энергии в тепло, называются активными сопротивлениями (обозначаются R). Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д. Индуктивность в цепи переменного тока: Пусть в цепи кроме источника периодически изменяющейся электродвижущей силы имеется индуктивность
Законы Кирхгофа Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа. П е р в ы й: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
где n – число ветвей, сходящихся в узле. В т о р о й: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
где m – число ветвей, образующих контур. Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1037; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.36 (0.006 с.) |

 или
или  , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной. . К такому режиму может быть отнесен и синусоидальный:
. К такому режиму может быть отнесен и синусоидальный: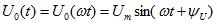
 - амплитуда;
- амплитуда; - начальная фаза;
- начальная фаза; - угловая скорость вращения ротора генератора.
- угловая скорость вращения ротора генератора. 314рад/с.
314рад/с. График синусоидальной функции называется волновой диаграммой.
График синусоидальной функции называется волновой диаграммой.



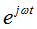 - поворотный множитель;
- поворотный множитель; - комплексная амплитуда напряжения;
- комплексная амплитуда напряжения; - сопряженная комплексная амплитуда напряжения.
- сопряженная комплексная амплитуда напряжения. будет представлять собой модуль или длину вектора напряжения.
будет представлять собой модуль или длину вектора напряжения. , сосредоточенная в катушке. Переменный ток в катушке индуктивности приводит к возникновению электродвижущей силы самоиндукции. Согласно закону Ома
, сосредоточенная в катушке. Переменный ток в катушке индуктивности приводит к возникновению электродвижущей силы самоиндукции. Согласно закону Ома .
Емкость в цепи переменного тока:
.
Емкость в цепи переменного тока:
 рис. 653
Конденсатор, подключенный к источнику постоянной ЭДС, полностью препятствует прохождения тока − за некоторый промежуток времени конденсатор заряжается, напряжение между его обкладками становится равным ЭДС источника, после чего ток в цепи прекращается. Если же конденсатор включен в цепь переменного тока, то ток в цепи не прекращается − фактически конденсатор периодически перезаряжается, заряды на его обкладках периодически изменяются как по величине, так и по знаку
рис. 653
Конденсатор, подключенный к источнику постоянной ЭДС, полностью препятствует прохождения тока − за некоторый промежуток времени конденсатор заряжается, напряжение между его обкладками становится равным ЭДС источника, после чего ток в цепи прекращается. Если же конденсатор включен в цепь переменного тока, то ток в цепи не прекращается − фактически конденсатор периодически перезаряжается, заряды на его обкладках периодически изменяются как по величине, так и по знаку
 , (2.8)
, (2.8) , (2.9)
, (2.9) (2.10)
(2.10)
 (2.11)
(2.11)



