
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Токи смещения. Теорема о циркуляции магнитного поля переменных токов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Если переменное магнитное поле создает поле электрическое, то разумно предположить существование и обратного процесса: изменяющееся электрическое поле порождает поле магнитное. Такое явление действительно существует и носит не совсем обычное название ток смещения По Максвеллу ток проводимости замыкается в конденсаторе током смещения
Точная формулировка В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения
В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:
где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения») Соответственно, плотностью тока смещения в вакууме называется величина
а в диэлектриках — величина
Теорема о циркуляции магнитного поля Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. Теорема о циркуляции утверждает, что циркуляция вектора В магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0на сумму всех токов, пронизывающих контур: Циркуляцией вектора магнитной индукции В по заданному контуру называется интеграл
Система уравнений Максвелла. Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Дифференциальная форма Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторных функций (
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные. Введённые обозначения: · · · · · · · ·
Интегральная форма При помощи формулы Остроградского — Гаусса и теоремы Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Введённые обозначения: · · · При интегрировании по замкнутой поверхности вектор элемента площади
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


 (с точностью до универсального постоянного коэффициента) называется[3] поток вектора быстроты изменения электрического поля
(с точностью до универсального постоянного коэффициента) называется[3] поток вектора быстроты изменения электрического поля  через некоторую поверхность[4]
через некоторую поверхность[4]  :
: (СИ)
(СИ)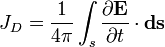 (СГС)
(СГС) (СИ)
(СИ) (СГС),
(СГС), (СИ)
(СИ)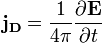 (СГС)
(СГС) (СИ)
(СИ)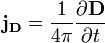 (СГС)
(СГС)
 ):
):






 — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);
— плотность стороннего электрического заряда (в единицах СИ — Кл/м³); — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как
— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как  , где
, где  — (средняя) скорость движения этих носителей в окрестности данной точки,
— (средняя) скорость движения этих носителей в окрестности данной точки,  — плотность заряда этого типа носителей (она в общем случае не совпадает с
— плотность заряда этого типа носителей (она в общем случае не совпадает с  )[29]; в общем случае это выражение надо усреднить по разным типам носителей;
)[29]; в общем случае это выражение надо усреднить по разным типам носителей; — скорость света в вакууме (299 792 458 м/с);
— скорость света в вакууме (299 792 458 м/с); — напряжённость электрического поля (в единицах СИ — В/м);
— напряжённость электрического поля (в единицах СИ — В/м); — напряжённость магнитного поля (в единицах СИ — А/м);
— напряжённость магнитного поля (в единицах СИ — А/м); — электрическая индукция (в единицах СИ — Кл/м²);
— электрическая индукция (в единицах СИ — Кл/м²); — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1); — дифференциальный оператор набла, при этом:
— дифференциальный оператор набла, при этом: означает ротор вектора,
означает ротор вектора, означает дивергенцию вектора.
означает дивергенцию вектора.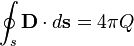

 , который окружает поверхность
, который окружает поверхность 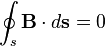

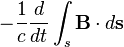
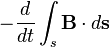
 , который является границей поверхности
, который является границей поверхности 


 — электрический заряд, заключённый в объёме
— электрический заряд, заключённый в объёме  — электрический ток, проходящий через поверхность
— электрический ток, проходящий через поверхность  направлен из объёма наружу. Ориентация
направлен из объёма наружу. Ориентация  .
.


