
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики магнитного поля в магнетикахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Магнитное поле в магнетиках
В общем случае для произвольного замкнутого контура l в магнетике по теореме о циркуляции вектора магнитной индукции (подразд. 1.6) имеем
Молекулярные токи, не охватывающие контур, дважды пересекают эту поверхность: один раз в одном направлении, другой раз – в противоположном. Вклад таких токов в суммарный ток
Если n – число атомов (молекул) в единице объема магнетика, то для суммарного тока, охватывающего элемент
где
Следовательно, выражение
Полную сумму молекулярных токов получим, проинтегрировав (3.20) по замкнутому контуру l:
Иными словами, циркуляция вектора намагничивания по произвольному замкнутому контуру равна алгебраической сумме молекулярных токов, проходящих через поверхность S, ограниченную этим контуром. Подстановка (3.21) в (3.19) приводит к выражению
откуда
Введем вектор напряженности магнитного поля
Равенство (3.23) является определением напряженности магнитного поля. Тогда для проекции напряженности магнитного поля на направление элементарного перемещения получаем
Подстановка (3.24) в (3.22) приводит к теореме о циркуляции напряженности магнитного поля:
Таким образом, циркуляция напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром. Если контур проведен внутри проводящей среды, в которой текут токи проводимости, то (3.25) удобно представить в виде
где Из (3.23) следует
Как показывает опыт, намагниченность
Коэффициент пропорциональности Подстановка (3.28) в (3.27) дает связь между напряженностью и магнитной индукцией:
где У диамагнетиков магнитные моменты атомов (молекул) и вектор намагниченности У парамагнетиков магнитные моменты атомов (молекул), вектор намагниченности Ферромагнетики Ферромагнетики имеют ряд особенностей, существенно отличающих их от других магнетиков. Для парамагнетиков и диамагнетиков зависимость намагниченности J от напряженности магнитного поля H носит линейный характер (3.28), где магнитная восприимчивость
Рис. 49 Рис. 50
На рис. 49 приведена кривая намагничивания ферромагнетика, первоначальный магнитный момент которого равен нулю. Эта кривая называется основной или нулевой кривой намагничивания. Если после достижения насыщения уменьшать напряженность магнитного поля, то уменьшение намагниченности следует не по первоначальной кривой, а выше нее (рис. 51). Когда напряженность внешнего поля станет равной нулю, намагниченность оказывается отличной от нуля. Соответствующая величина Намагниченность становится равной нулю (рис. 51) только под действием поля Дальнейшее изменение напряженности магнитного поля приводит к изображенной на рис. 51 зависимости
Можно показать, что при обходе по петле гистерезиса совершается работа, идущая, в частности, на нагревание ферромагнетика и пропорциональная площади петли гистерезиса Ферромагнетики с большой остаточной намагниченностью, большой остаточной индукцией ( Ферромагнетики с малой коэрцитивной силой ( При нагреве ферромагнетик теряет свои характерные свойства и становится парамагнетиком. Температура, при которой это происходит, называется точкой Кюри Теория ферромагнетизма была создана Френкелем и Гейзенбергом в 1928 г. В основе теории лежит представление о том, что за магнитные свойства ферромагнетиков ответственны собственные (спиновые) магнитные моменты электронов. При определенных условиях в кристаллах могут возникать силы (в квантовой механике эти силы называются обменными), которые приводят к выстраиванию магнитных моментов электронов параллельно друг другу. В результате возникают области спонтанного (самопроизвольного) намагничивания – домены. Линейные размеры доменов составляют 1–100 мкм.
 , за счет уменьшения размеров соседних доменов, у которых угол между магнитным моментом и , за счет уменьшения размеров соседних доменов, у которых угол между магнитным моментом и  тупой. С ростом тупой. С ростом  домены, ориентация магнитных моментов которых сильно отличается от направления домены, ориентация магнитных моментов которых сильно отличается от направления  , продолжают уменьшаться и наконец исчезают совсем. , продолжают уменьшаться и наконец исчезают совсем.  , т. е. в сильном магнитном поле, происходит поворот магнитных моментов доменов в направлении внешнего поля. В результате магнитные моменты всех доменов ориентируются в направлении внешнего магнитного поля. Наступает насыщение, и дальнейшее увеличение напряженности поля не изменяет намагниченности ферромагнетика. , т. е. в сильном магнитном поле, происходит поворот магнитных моментов доменов в направлении внешнего поля. В результате магнитные моменты всех доменов ориентируются в направлении внешнего магнитного поля. Наступает насыщение, и дальнейшее увеличение напряженности поля не изменяет намагниченности ферромагнетика.Процессы изменения доменной структуры ферромагнетика носят необратимый характер. Это лежит в основе объяснения наблюдаемой петли гистерезиса. Нагревание ферромагнетика приводит к тепловому разрушению его доменной структуры, при этом ферромагнетик превращается в парамагнетик. В заключение отметим, что рост одних доменов и уменьшение других не означает перемещение атомов, т. е. перенос вещества в ферромагнетике. Происходит только изменение ориентации собственных магнитных моментов электронов домена на границе с соседним доменом.
Как и у ферромагнетиков, у антиферромагнетиков и ферримагнетиков при нагреве выше определенной температуры (у антиферромагнетиков она называется температурой Нееля) нарушается упорядоченность структуры расположения магнитных моментов атомов и они превращаются в парамагнетики.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.008 с.) |

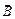 является результатом суперпозиции внешнего поля
является результатом суперпозиции внешнего поля 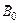 и собственного магнитного поля магнетика
и собственного магнитного поля магнетика 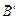 :
: 
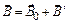 .
. . (3.19)
. (3.19) Ток, охватываемый контуром l, представлен как алгебраическая сумма токов проводимости
Ток, охватываемый контуром l, представлен как алгебраическая сумма токов проводимости  и алгебраическая сумма молекулярных токов Ампера
и алгебраическая сумма молекулярных токов Ампера  , проходящих через поверхность S, ограниченную контуром l (рис. 47).
, проходящих через поверхность S, ограниченную контуром l (рис. 47). Найдем вклад
Найдем вклад  токов, которые охватывают малый элемент
токов, которые охватывают малый элемент  контура. Построим косой цилиндр, ось которого совпадает с
контура. Построим косой цилиндр, ось которого совпадает с  , ограниченной молекулярным током. Как видно из рис. 48, элемент контура
, ограниченной молекулярным током. Как видно из рис. 48, элемент контура 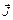 угол
угол 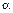 , охватывается теми молекулярными токами, центры которых попадают внутрь косого цилиндра объемом dV, который определяется формулой
, охватывается теми молекулярными токами, центры которых попадают внутрь косого цилиндра объемом dV, который определяется формулой .
. ,
, – сила молекулярного тока, магнитный момент которого
– сила молекулярного тока, магнитный момент которого .
. представляет собой магнитный момент единицы объема, т. е. модуль вектора
представляет собой магнитный момент единицы объема, т. е. модуль вектора  =
=  , где
, где  . Таким образом, для суммарного молекулярного тока, охватывающего элемент
. Таким образом, для суммарного молекулярного тока, охватывающего элемент  . (3.20)
. (3.20) . (3.21)
. (3.21) ,
, . (3.22)
. (3.22) . (3.23)
. (3.23) . (3.24)
. (3.24) . (3.25)
. (3.25) , (3.26)
, (3.26) – проекция вектора плотности тока проводимости на направление нормали к элементу поверхности
– проекция вектора плотности тока проводимости на направление нормали к элементу поверхности  .
. . (3.27)
. (3.27) . (3.28)
. (3.28) называется магнитной восприимчивостью.
называется магнитной восприимчивостью. ,
,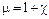 называется магнитной проницаемостью вещества. Магнитная восприимчивость
называется магнитной проницаемостью вещества. Магнитная восприимчивость  – величины, характеризующие магнитные свойства диамагнетиков и парамагнетиков.
– величины, характеризующие магнитные свойства диамагнетиков и парамагнетиков. ,
,  .
. ,
,  . С ростом температуры магнитная восприимчивость уменьшается (
. С ростом температуры магнитная восприимчивость уменьшается ( – закон Кюри).
– закон Кюри). для ферромагнетика. В этом случае увеличение напряженности магнитного поля от нуля сопровождается нелинейным ростом величины намагниченности ферромагнетика до некоторого предельного значения, по достижении которого намагниченность не меняется. Предельное намагничивание характеризуется величиной
для ферромагнетика. В этом случае увеличение напряженности магнитного поля от нуля сопровождается нелинейным ростом величины намагниченности ферромагнетика до некоторого предельного значения, по достижении которого намагниченность не меняется. Предельное намагничивание характеризуется величиной  и называется насыщением намагничивания.
и называется насыщением намагничивания.
 Нелинейный характер зависимости
Нелинейный характер зависимости  достигает максимального значения
достигает максимального значения  (сравните с диамагнетиками и парамагнетиками).
(сравните с диамагнетиками и парамагнетиками). называется остаточной намагниченностью.
называется остаточной намагниченностью. , имеющего направление, противоположное полю, вызвавшему первоначальное намагничивание. Напряженность
, имеющего направление, противоположное полю, вызвавшему первоначальное намагничивание. Напряженность 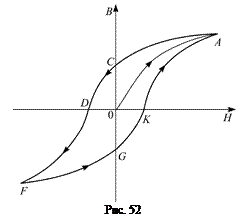 Зависимость магнитной индукции
Зависимость магнитной индукции  от напряженности поля
от напряженности поля  в общем случае также имеет вид гистерезиса (рис. 52). Стрелки и буквы O - A - C - D - F - G - K указывают последовательность изменения состояния намагничивания ферромагнетика.
в общем случае также имеет вид гистерезиса (рис. 52). Стрелки и буквы O - A - C - D - F - G - K указывают последовательность изменения состояния намагничивания ферромагнетика. .
. ) и большой коэрцитивной силой (
) и большой коэрцитивной силой ( ) называются жесткими ферромагнетиками. Для них характерна широкая петля гистерезиса, и они применяются для создания постоянных магнитов.
) называются жесткими ферромагнетиками. Для них характерна широкая петля гистерезиса, и они применяются для создания постоянных магнитов. ), т. е. с узкой петлей гистерезиса, называются мягкими. Они имеют малые потери на нагревание и применяются в электротехнике, например, для изготовления сердечников трансформаторов.
), т. е. с узкой петлей гистерезиса, называются мягкими. Они имеют малые потери на нагревание и применяются в электротехнике, например, для изготовления сердечников трансформаторов. . Для железа
. Для железа  1040 К.
1040 К. Если ферромагнетик первоначально не намагничен, то магнитные моменты отдельных доменов ориентированы произвольно, и намагниченность
Если ферромагнетик первоначально не намагничен, то магнитные моменты отдельных доменов ориентированы произвольно, и намагниченность  Имеются вещества, в которых магнитные свойства также обусловлены обменными силами, характеризующими взаимодействие спиновых магнитных моментов электронов в атомах, но которые существенно отличаются от ферромагнетиков. Существуют материалы, у которых спиновые магнитные моменты электронов у соседних атомов выстраиваются антипараллельно друг другу, поскольку это соответствует состоянию с наименьшей энергией. Если при этом магнитные моменты соседних атомов одинаковы по величине, то они компенсируют друг друга и результирующий магнитный момент магнетика в отсутствие внешнего поля становится равным нулю. Такие вещества называются антиферромагнетиками (примером являются марганец, хром и некоторые другие металлы, некоторые окислы металлов). Кристаллическую решетку антиферромагнетика можно представить как совокупность
Имеются вещества, в которых магнитные свойства также обусловлены обменными силами, характеризующими взаимодействие спиновых магнитных моментов электронов в атомах, но которые существенно отличаются от ферромагнетиков. Существуют материалы, у которых спиновые магнитные моменты электронов у соседних атомов выстраиваются антипараллельно друг другу, поскольку это соответствует состоянию с наименьшей энергией. Если при этом магнитные моменты соседних атомов одинаковы по величине, то они компенсируют друг друга и результирующий магнитный момент магнетика в отсутствие внешнего поля становится равным нулю. Такие вещества называются антиферромагнетиками (примером являются марганец, хром и некоторые другие металлы, некоторые окислы металлов). Кристаллическую решетку антиферромагнетика можно представить как совокупность  двух встроенных друг в друга подрешеток. У каждой из подрешеток магнитные моменты атомов ориентированы параллельно друг другу, но противоположно магнитным моментам атомов другой подрешетки (рис. 54). Магнитная восприимчивость антиферромагнетиков очень мала.
двух встроенных друг в друга подрешеток. У каждой из подрешеток магнитные моменты атомов ориентированы параллельно друг другу, но противоположно магнитным моментам атомов другой подрешетки (рис. 54). Магнитная восприимчивость антиферромагнетиков очень мала. У некоторых материалов, однако, намагниченности подрешеток неодинаковы (например, из-за разной структуры соседних атомов) (рис. 55). Вследствие этого появляется результирующая намагниченность. Такие материалы называются ферримагнетиками. Магнитные свойства ферримагнетиков похожи на свойства ферромагнетиков (у них, например, большая магнитная восприимчивость, имеет место явление гистерезиса), но проявляются слабее. Многие ферримагнетики являются полупроводниками и обладают малой электропроводностью. Такие ферримагнетики называются ферритами. Являясь достаточно сильными магнетиками, они имеют малые тепловые потери при работе на высоких частотах.
У некоторых материалов, однако, намагниченности подрешеток неодинаковы (например, из-за разной структуры соседних атомов) (рис. 55). Вследствие этого появляется результирующая намагниченность. Такие материалы называются ферримагнетиками. Магнитные свойства ферримагнетиков похожи на свойства ферромагнетиков (у них, например, большая магнитная восприимчивость, имеет место явление гистерезиса), но проявляются слабее. Многие ферримагнетики являются полупроводниками и обладают малой электропроводностью. Такие ферримагнетики называются ферритами. Являясь достаточно сильными магнетиками, они имеют малые тепловые потери при работе на высоких частотах.


