
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность магнитного поляСодержание книги Поиск на нашем сайте Ротор результирующего поля в магнетике
Учтем, что ротор внешнего поля
где Аналогично тому, как для описания электриРческого поля в диэлектриках используется вспомогательная величина – вектор электрической индукции
токов, и суммарный поток, создаваемый ими равен:
где Теперь необходимо учесть, что произведение
Соответственно поток плотности молекулярных токов через всю поверхность
По теореме Стокса
а значит
Таким образом,
Теперь приходим к следующему соотношению для ротора результирующего поля в магнетике Объединим роторы
Объединим роторы в (19.11) и получим, что
Ротор величины, в круглых скобках в (19.12) определяется плотностью только макроскопических токов, и ее, по определению, называют напряженностью магнитного поля:
Теорема о циркуляции вектора напряженности магнитного поля Теоремой о циркуляции
Поток
Интеграл в правой части соотношения (19.15) представляет собой общий ток через поверхность
Это соотношение и называют теоремой о циркуляции вектора напряженности электрического поля.
Магнитная проницаемость Для характеристики магнитных свойств среды используется параметр
Для большинства веществ в не очень сильных полях магнитная восприимчивость Подставим значение намагниченности
Выразим напряженность поля из (19.18):
Величину
Тогда соотношение (19.19) приводится к виду:
И можно утверждать, что напряженность магнитного поля есть вектор, направленный также, как индукция, но в Виды магнетиков. Традиционно по величине магнитной восприимчивости (и соответственно магнитной проницаемости) вещества делят на три группы диамагнетики, парамагнетики и ферромагнетики. У диамагнетиков У парамагнетиков У ферромагнетиков Природа молекулярных токов Природу молекулярных токов и диамагнетизма можно объяснить в рамках представлений теории Бора, согласно которой электроны в атомах движутся по избранным стационарным орбитам. При таком движении электрон Отношение магнитного момента частицы к ее механическому моменту является характерным параметром микрочастиц и называется гиромагнитным отношением. Для орбитального движения электрона (с учетом противоположного направления моментов)
Спин электрона Наличие у электрона одновременно магнитного и механического моментов обусловливает существование магитомеханических и механомагнитных явлений. Существование магитомеханических явлений было экспериментально подтверждено опытами Эйнштейна и де Хааса. Рассматривая парамагнитное тело как замкнутую систему, следует предположить, что при помещении тела в магнитное поле происходит ориентация магнитных моментов электронов полем. Механический момент электронной подсистемы тела становится отличным от нуля. В силу закона сохранения момента импульса тело должно приобрести противоположный момент импульса, т.е. начать вращаться. В опытах Эйнштейна и де Хааса удалось наблюдать возникновение вращательных колебаний железного стержня в переменном магнитном поле. Барнет наблюдал механомагнитное явление, заключавшееся в возникновении намагниченности у железного стержня, приведенного в очень быстрое вращение. Вращение приводит к ориентации механических моментов электронов в направлении оси вращения. Сопутствующая ориентация магнитных моментов проявляется в намагничении вещества. Барнету удалось экспериментально измерить гиромагнитное отношение для электронов. Полученное значение соответствовало
т.е. в два раза превысило ожидаемое. Впоследствии было установлено, что ферромагнитные свойства железа обусловлены не орбитальными магнитными моментами электронов, а так называемыми спиновыми магнитными моментами. Каждый электрон наряду с зарядом и массой обладает собственным моментом импульса и соответствующим магнитным моментами, которые следует рассматривать как неотъемлемое свойство электрона (и многих других элементарных частиц). Эти моменты называют спиновыми вследствие того, что первоначально было предположение (ошибочное!), что они связаны с вращением электрона вокруг собственной оси. Спин (механический момент) элементарных частиц оказался кратным величине постоянной Планка
Эту величину называют магнетоном Бора.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 . (19.3)
. (19.3) определяется плотностью макроскопического тока
определяется плотностью макроскопического тока  . Аналогичное соотношение справедливо и для поля создаваемого магнетиком:
. Аналогичное соотношение справедливо и для поля создаваемого магнетиком: . (19.3)
. (19.3) - плотность молекулярных токов.
- плотность молекулярных токов. , для
, для  описания магнитного поля в магнетиках используется напряженность электрического поля
описания магнитного поля в магнетиках используется напряженность электрического поля  . Чтобы сформулировать ее определение необходимо выразить плотность молекулярных токов через вектор намагниченности
. Чтобы сформулировать ее определение необходимо выразить плотность молекулярных токов через вектор намагниченности  . С этой целью найдем поток плотности молекулярных токов через некоторую поверхность
. С этой целью найдем поток плотности молекулярных токов через некоторую поверхность 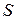 , опирающуюся на контур
, опирающуюся на контур 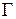 (рисунок 19.1). При этом необходимо учесть, что поток создают только токи, нанизанные на контур
(рисунок 19.1). При этом необходимо учесть, что поток создают только токи, нанизанные на контур  На элемент
На элемент  контура нанизываются те токи, центры которых попадают
контура нанизываются те токи, центры которых попадают  внутрь косого цилиндра с высотой
внутрь косого цилиндра с высотой 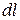 и основанием, равным площади молекулярного тока
и основанием, равным площади молекулярного тока  . Объем такого цилиндра равен
. Объем такого цилиндра равен  . Если концентрация молекулярных токов
. Если концентрация молекулярных токов 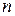 , то в этот объем попадают токи
, то в этот объем попадают токи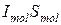
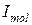 - сила молекулярного тока.
- сила молекулярного тока. – магнитному моменту молекулярного тока. А его произведение на концентрацию дает магнитный момент единицы объема, т.е. модуль вектора намагниченности. Поэтому поток, создаваемый молекулярными токами, нанизанными на элемент
– магнитному моменту молекулярного тока. А его произведение на концентрацию дает магнитный момент единицы объема, т.е. модуль вектора намагниченности. Поэтому поток, создаваемый молекулярными токами, нанизанными на элемент  (19.6)
(19.6) (19.7)
(19.7) , (19.8)
, (19.8) . (19.9)
. (19.9) . (19.10)
. (19.10) . (19.11)
. (19.11)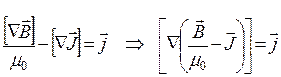 . (19.12)
. (19.12) . (19.13)
. (19.13) . (19.14)
. (19.14) через некоторую поверхность
через некоторую поверхность 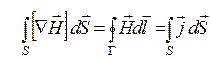 . (19.15)
. (19.15)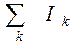 . Это есть те проводники, которые охватываются контуром
. Это есть те проводники, которые охватываются контуром 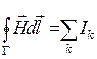 . (19.16)
. (19.16) , который называют магнитной восприимчивостью (аналогичный диэлектрической восприимчивости
, который называют магнитной восприимчивостью (аналогичный диэлектрической восприимчивости  в соотношении
в соотношении  ). Традиционно намагниченность
). Традиционно намагниченность  . (19.17)
. (19.17)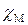 , равная произведению
, равная произведению  вещества:
вещества:  .
. . (19.18)
. (19.18) . (19.19)
. (19.19)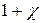 обозначают
обозначают 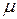 и называют относительной магнитной проницаемостью:
и называют относительной магнитной проницаемостью: . (19.20)
. (19.20) , (19.21)
, (19.21) раз меньший. Однако необходимо иметь в виду, что это утверждение перестает быть справедливым в анизотропных средах.
раз меньший. Однако необходимо иметь в виду, что это утверждение перестает быть справедливым в анизотропных средах. . Это означает, что вектор намагниченности в них направлен навстречу напряженности внешнего поля.
. Это означает, что вектор намагниченности в них направлен навстречу напряженности внешнего поля. .
. . Кроме того ферромагнетики имеют еще ряд особенностей, которые мы рассмотрим позднее. Необходимо отметить, что при повышении температуры ферромагнетики изменяют свои свойства и при характерной для каждого вещества критической температуре переходят в парамагнитное состояние, т.е. становятся парамагнетиками. Можно считать ферромагнетики частным случаем парамагнетиков, которые при понижении температуры испытывают фазовый переход в ферромагнитное состояние.
. Кроме того ферромагнетики имеют еще ряд особенностей, которые мы рассмотрим позднее. Необходимо отметить, что при повышении температуры ферромагнетики изменяют свои свойства и при характерной для каждого вещества критической температуре переходят в парамагнитное состояние, т.е. становятся парамагнетиками. Можно считать ферромагнетики частным случаем парамагнетиков, которые при понижении температуры испытывают фазовый переход в ферромагнитное состояние. оказывается эквивалентным волчку (гироскопу) и характеризуется механическим моментом импульса
оказывается эквивалентным волчку (гироскопу) и характеризуется механическим моментом импульса 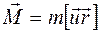 , направленным перпендикулярно плоскости орбиты и связанным с направлением движения правилом правого винта. Вращающийся по орбите электрон создает замкнутый круговой электрический ток. Направление этого тока противоположно скорости движения электрона в силу отрицательности его заряда. Величина тока определяется зарядом, переносимым электроном в единицу времени. Если частота обращения электрона равна
, направленным перпендикулярно плоскости орбиты и связанным с направлением движения правилом правого винта. Вращающийся по орбите электрон создает замкнутый круговой электрический ток. Направление этого тока противоположно скорости движения электрона в силу отрицательности его заряда. Величина тока определяется зарядом, переносимым электроном в единицу времени. Если частота обращения электрона равна  , то в единицу времени он переносит заряд
, то в единицу времени он переносит заряд  , т.е. создает ток силой
, т.е. создает ток силой  . Вектор магнитного момента
. Вектор магнитного момента 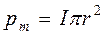 этого кругового тока связан правилом правого винта не со скоростью электрона, а с силой тока и направлен противоположно
этого кругового тока связан правилом правого винта не со скоростью электрона, а с силой тока и направлен противоположно  . Магнитный и механический моменты электрона обусловлены движением электрона по орбите и называются орбитальными.
. Магнитный и механический моменты электрона обусловлены движением электрона по орбите и называются орбитальными. (19.22)
(19.22) , (19.23)
, (19.23) , которой считают естественной единицей момента импульса. У электронов спин
, которой считают естественной единицей момента импульса. У электронов спин 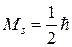 . Говорят, что электрон принадлежит к числу частиц полуцелым спином. Подставив это значение в формулу (19.23), для спинового магнитного момента электрона найдем:
. Говорят, что электрон принадлежит к числу частиц полуцелым спином. Подставив это значение в формулу (19.23), для спинового магнитного момента электрона найдем: . (19.24)
. (19.24)


