
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле. Магнитная индукция.Содержание книги Поиск на нашем сайте
На правах рукописи Физика Конспект лекций (Часть 4. Электромагнитные явления)
Для студентов направления 230400 «Информационные системы и технологии»
Электронный образовательный ресурс
Составитель: к.ф.-м.н., доцент В.В. Коноваленко
Рассмотрен и рекомендован для использования в учебном процессе на 2013/2014 – 2015/2016 уч. г. на заседании кафедры ЕНД. Протокол № 1 от 04. 09. 2013 г.
Шахты 2013
МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ Взаимодействие токов Самостоятельно: § 39. Магнитное поле. Магнитная индукция. Экспериментально установлено, что при пропускании электрического тока по двум параллельным проводникам они, в зависимости от направлений токов, либо притягиваются, либоотталкиваются. Протекающий по проводнику ток оказывает ориентирующее действие на магнитную стрелку. Таким образом, при протекании по проводнику тока свойства окружающего пространства изменяются: в нем возникает магнитное поле, посредством которого осуществляется взаимодействие проводника с током с другими токами, магнитной стрелкой и т. п. Из опыта следует, что магнитное поле имеет направленный характер, а значит должно характеризоваться некоторой векторной величиной. Аналогично магнитной стрелке магнитное ноле оказывает ориентирующее действие и на замкнутый контур с током. Магнитные свойства плоского замкнутого контура с током можно охарактеризовать его магнитным моментом
где
Положительной нормалью называют нормаль, связанную с направлением тока в контуре правилом правого винта. В магнитном поле на контур с током действует вращательный момент По определению магнитной индукцией будем называть вектор
а направление совпадает с направлением магнитного момента контура в положении равновесия. Отличие проводника с током от просто проводника заключается только в том, что в проводнике с током имеется направленное движение электрических зарядов. Следовательно, магнитное поле порождается только движущимися зарядами. Аналогично, поскольку магнитное поле действует только на проводники с током, можно утверждать, что магнитное поле воздействует только на движущиеся заряды. Экспериментально установлено, что для магнитного поля справедлив принцип суперпозиции: поле, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей Закон Био-Савара-Лапласа. Закон БСЛ позволяет вычислить индукцию поля в произвольной точке, которая создается проводников с током I. Элемент проводника длиной
Среднее по всем носителям тока в элементе
Умножив (18.7) на количество носителей тока в
Поскольку
Соответственно получаем:
Соотношение (18.11) называется законом Био-Савара-Лапласа. Вычисление индукции поля прямого тока Индукция поля прямого тока находится по формуле Сила Лоренца На движущийся в магнитном поле заряд действует сила, которую естественно называть магнитной. Логично предположить, что эта сила должна быть пропорциональна величине заряда q, его скорости
Отметим, что, в соответствии с определением, магнитная сила всегда перпендикулярна скорости заряда и индукции поля, а значит - работы над зарядом не совершает. (18.А = 0) Если на заряженную частицу одновременно действуют электрическое и магнитное поля, то результирующая сила будет равна
Эта сила называется силой Лоренца. Закон Ампера Закон Ампера определяет силу, действующую на проводник с током в магнитном поле. Получим формулу закона Ампера, исходя из выражения для силы Лоренца. На каждый из носителей тока в проводнике, находящемся в магнитном поле действует сила
За счет взаимодействия носителей тока с остальным веществом проводника эта сила передается всему проводнику в целом. Усредняя силу (18.14) по всем носителям тока находящимся в элементе
Число носителей тока в элементе
Учтем, что
Формула (18.17) определяет силу, действующую на элемент тока Дивергенция магнитного поля До настоящего времени экспериментально обнаружить магнитные заряды не удалось. Соответственно линии вектора
– поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Преобразуем поверхностный интеграл в (18.40) по теореме Остроградского-Гаусса:
Уравнение (18.41) должно выполняться для произвольного объема, а поэтому
Соотношение (18.42)выражает теорему Гаусса в дифференциальной форме для вектора индукции магнитного поля. Ротор магнитного поля
Тогда для циркуляции получаем
Если рассматриваемый контур охватывает ток, то при обходе по контуру радиальная прямая поворачивается в одном направлении и
где под I подразумевается ток, охватываемый контуром. В выражении (18.45) ток рассматривается как алгебраическая величина: если направление обхода контура образует с направлением тока правовинтовую систему, то ток считают положительным, в противном случае - отрицательным. Формула (18.45) получена для прямого тока. Но можно доказать, что онасправедлива и в общем случае, для тока произвольной формы.
По формуле (18.45)
Важно помнить, что сумма в (18.47) является алгебраической. Возможны ситуации, когда токи распределены в пространстве с некоторой плотностью
По теореме Стокса
Следовательно
Поверхность интегрирования может быть произвольной (опирающуйся на контур L), поэтому должны быть равны подынтегральные выражения:
Формулы (18.48) и (18.51) отражают существенное отличие электрического и магнитного полей: циркуляция и ротор вектора напряженности электрического поля равны нулю. Это является следствием того, что электростатическое поле потенциально и может быть описано с помощью скалярного потенциала. Магнитное поле не является потенциальным, его циркуляция не обязательно равна нулю, его нельзя описать с помощью скалярного потенциала. Такие поля называют вихревыми или соленоидальными. Поле соленоида и тороида. Самостоятельно. Обратить внимание на вид силовых линий этих полей и формулы для индукции. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ Магнитная проницаемость Для характеристики магнитных свойств среды используется параметр
Для большинства веществ в не очень сильных полях магнитная восприимчивость Подставим значение намагниченности
Выразим напряженность поля из (19.18):
Величину
Тогда соотношение (19.19) приводится к виду:
И можно утверждать, что напряженность магнитного поля есть вектор, направленный также, как индукция, но в Виды магнетиков. Традиционно по величине магнитной восприимчивости (и соответственно магнитной проницаемости) вещества делят на три группы диамагнетики, парамагнетики и ферромагнетики. У диамагнетиков У парамагнетиков У ферромагнетиков Природа молекулярных токов Природу молекулярных токов и диамагнетизма можно объяснить в рамках представлений теории Бора, согласно которой электроны в атомах движутся по избранным стационарным орбитам. При таком движении электрон Отношение магнитного момента частицы к ее механическому моменту является характерным параметром микрочастиц и называется гиромагнитным отношением. Для орбитального движения электрона (с учетом противоположного направления моментов)
Спин электрона Наличие у электрона одновременно магнитного и механического моментов обусловливает существование магитомеханических и механомагнитных явлений. Существование магитомеханических явлений было экспериментально подтверждено опытами Эйнштейна и де Хааса. Рассматривая парамагнитное тело как замкнутую систему, следует предположить, что при помещении тела в магнитное поле происходит ориентация магнитных моментов электронов полем. Механический момент электронной подсистемы тела становится отличным от нуля. В силу закона сохранения момента импульса тело должно приобрести противоположный момент импульса, т.е. начать вращаться. В опытах Эйнштейна и де Хааса удалось наблюдать возникновение вращательных колебаний железного стержня в переменном магнитном поле. Барнет наблюдал механомагнитное явление, заключавшееся в возникновении намагниченности у железного стержня, приведенного в очень быстрое вращение. Вращение приводит к ориентации механических моментов электронов в направлении оси вращения. Сопутствующая ориентация магнитных моментов проявляется в намагничении вещества. Барнету удалось экспериментально измерить гиромагнитное отношение для электронов. Полученное значение соответствовало
т.е. в два раза превысило ожидаемое. Впоследствии было установлено, что ферромагнитные свойства железа обусловлены не орбитальными магнитными моментами электронов, а так называемыми спиновыми магнитными моментами. Каждый электрон наряду с зарядом и массой обладает собственным моментом импульса и соответствующим магнитным моментами, которые следует рассматривать как неотъемлемое свойство электрона (и многих других элементарных частиц). Эти моменты называют спиновыми вследствие того, что первоначально было предположение (ошибочное!), что они связаны с вращением электрона вокруг собственной оси. Спин (механический момент) элементарных частиц оказался кратным величине постоянной Планка
Эту величину называют магнетоном Бора.
Природа ферромагнетизма
Природа ферромагнетизма весьма сложна и связана с квантовомеханическим описанием свойств твердых тел. В кристаллах ферромагнетиков между атомами возникает специфическое обменное взаимодействие, которое стремится установить магнитные моменты атомов в одном направлении жесткому выстраиванию магнитных моментов противостоит тепловое движение, которое вносит хаос в распределение магнитных моментов атомов по направлениям. С понижении температуры (напомним, что при высоких температурах ферромагнетик находится в парамагнитном состоянии) при определенной температуре (температуре Кюри), характерной для кристаллов данного состава, обменное взаимодействие начинает преобладать. Магнитные моменты атомов ферромагнетика выстраиваются в определенном направлении, кристалл самопроизвольно намагничивается. Этот процесс называют возникновением спонтанной намагниченности. Реально описанный процесс не наблюдается. Это связано с тем, что при выстраивании в определенном направлении всех магнитных моментов атомов, образец кристалла создавал вы в окружающем пространстве сильное магнитное поле. С полем связана энергия, и такое состояние оказывается энергетически невыгодным. Поэтому кристалл разбивается на небольшие области, в пределах которых магнитные моменты атомов действительно параллельны, и намагниченность максимальна. Эти область называются доменами.
Однако с границами доменов связана дополнительная энергия, и состояние с очень маленькими доменами оказывается энергетически невыгодным. Поэтому кристалл переходит в энергетически оптимальное состояние, в котором размеры доменов составляют от одного до десяти микрон. Важно при этом, что в пределах домена кристалл предельно намагничен. Поэтому внешнему полю достаточно сместить границы доменов, и возникнет очень большая намагниченность. Смещение границ доменов с увеличение напряженности внешнего поля схематически показано на рисунке. В больших полях кристалл переходит в монодоменное состояние. Вблизи насыщения основной кривой намагнничения намагниченность одного домена поворачивается в направлении внешнего поля. После завершения этого процесса дальнейшее существенное увеличение намагниченности оказывается невозможным, зависимость насыщается. При повышении температуры кристалла до температуры Кюри, т.е. температуры возникновения спонтанной намагниченности, тепловое движение разрушает магнитную упорядоченность, разрушается спонтанная намагниченность, исчезают домены, кристалл становится парамагнетиком. В этом состоянии магнитная восприимчивость продолжает уменьшаться с ростом температуры по закону Кюри-Вейсса:
где ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ Токи Фуко Индукционные токи могут возникать не только в контурах, но и в сплошных массивных проводниках. Действительно, всякий сплошной проводник можно представить состоящим из большого количества замкнутых контуров. В этом случае индукционные токи называют вихревыми или токами Фуко. По правилу Ленца вихревые токи направлены так, чтобы противодействовать причине их вызывающей. Поэтому движущиеся в магнитном поле сплошные проводники испытывают сильное торможение, величина которого зависит от скорости движения. Это используют, например, для торможения подвижных частей стрелочных приборов. При этом торможение уменьшается по мере приближения стрелки к положению равновесия. В индукционных печах вихревые токи обеспечивают разогрев металлов до плавления. Однако в трансформаторах индукционные токи приводят к дополнительным потерям энергии на разогрев сердечника, и с ними борются, набирая сердичники из изолированных пластин. При протекании по проводам тока создается магнитное поле, и носители заряда движутся в этом поле. Если ток переменный, то возникающие токи Токи Фуко увеличивают его вблизи поверхности провода и уменьшают в центре. В результате большая часть переменного тока протекает по поверхности проводника. Это явление называют поверхностным, или скин-эффектом. Явление самоиндукции Явление самоиндукции является частным случаем явления электромагнитной индукции. Если в некотором контуре протекает электрический ток, то он создает магнитное поле и магнитный поток через поверхность контура. При изменениях тока изменяется магнитный поток, и возникает ЭДС индукции противодействующая этому изменению по правилу Ленца. Ее и называют ЭДС индукции Величина индукции магнитного поля, а значит и магнитный поток через его поверхность, пропорциональны протекающему току:
Коэффициент пропорциональности в формуле (20.10) называется индуктивностью контура. Единицей индуктивности является 1 генри (Гн). Индуктивность определяется геометрическими параметрами контура и магнитными свойствами окружающей среды. Для того, чтобы более конкретно представить влияние на величину индуктивности этих факторов вычислим индуктивность соленоида, близкого к идеальному, т.е. с длиной
где
Количество витков в соленоиде
Потокосцепление (полный поток)
Очевидно, что индуктивность соленоида выражается соотношением
где Если в области действия магнитного поля ферромагнетики отсутствуют, то магнитная проницаемость остается постоянной и ЭДС индукции
20.5. Влияние самоиндукции на протекание тока в цепи очень наглядно демонстрируется характером изменения тока в цепи, содержащей индуктивность и активное сопротивление при ее подключении и отключении от источника тока. В положении переключателя, показанном на рисунке, в цепи идет ток
Предположим, что в некоторый момент времени
Разделим на
Разделим в (20.17) переменные:
После интегрирования получаем:
Потенцирование этого соотношения дает зависимость тока от времени:
При
Явление взаимной индукции
Допустим, что имеются два контура, расположенные недалеко друг от друга, так что магнитные поля, создаваемые каждым из них, создают через витки другого контура ощутимый магнитный поток. Обозначим магнитный поток, создаваемый первым контуром с током
Аналогичным образом ток второго контура создает через витки первого поток
Контуры в этом в этом случае называют связанными. При изменениях тока в одном из контуров в другом индуцируется ЭДС взаимной индукции соответственно
Энергия магнитного поля В цепи, показанной на рисунке, в исходном состоянии течет ток по индуктивности В процессе уменьшения тока за время
Если индуктивность катушки остается постоянной, то
Ток в индуктивности спадает от некоторого значения I до нуля, поэтому вся работа за время исчезновения тока
Именно такой энергией обладает магнитное поле катушки при прохождении по ней тока:
Для идеального соленоида (катушки)
Поле идеального соленоида сосредоточено внутри соленоида, поэтому можно утверждать, что с магнитным полем связана энергия, распределенная в пространстве с плотностью
Вихревое электрическое поле Говоря о природе ЭДС индукции, мы связали ее возникновение с действием силы Лоренца на заряды в движущемся проводнике. Однако для покоящегося контура, расположенного в изменяющемся магнитном поле, такое объяснение является неприемлемым. Тем не менее, ЭДС индукции возникает! Возникновение индукционного тока в замкнутом контуре при изменении магнитного потока, связанном с изменением внешнего поля обусловлено действием неких сторонних сил, которые не связаны ни с химическими превращениями в контуре, ни с магнитными силами. Поэтому будем считать, что в рассматриваемом случае ток в контуре возникает за счет действия электрического поля с напряженностью
Поскольку
Поскольку рассматриваемый контур предполагается неподвижным, дифференцирование по времени можно поменять местами:
По теореме Стокса
Поэтому
Поверхность интегрирования произвольна, поэтому должны быть равны подынтегральные выражения:
Итак, ротор поля Одна из важнейших идей Максвелла заключалась в том, что он предположил, что изменяющееся во времени магнитное поле создает в окружающем пространстве вихревое электрическое поле независимо от наличия в данной точке пространства про |
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.97 (0.011 с.) |

 :
: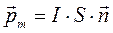 (18.1)
(18.1) - сила тока в контуре;
- сила тока в контуре;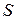 - площадь контура;
- площадь контура; - положительная единичная нормаль к контуру.
- положительная единичная нормаль к контуру. , величина которого зависит от ориентации контура в пространстве. При некоторой ориентации модуль
, величина которого зависит от ориентации контура в пространстве. При некоторой ориентации модуль  достигает максимального значения. Отношение
достигает максимального значения. Отношение  не зависит от
не зависит от  . Таким образом, действие магнитного поля на контур с током может быть использовано для определения векторной характеристики магнитного поля, аналогичной напряженности электростатического поля.
. Таким образом, действие магнитного поля на контур с током может быть использовано для определения векторной характеристики магнитного поля, аналогичной напряженности электростатического поля.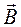 , модуль которого
, модуль которого , (18.2)
, (18.2) , порождаемых каждым зарядом в отдельности:
, порождаемых каждым зарядом в отдельности: 
 и сечением
и сечением  содержит
содержит  носителей тока (
носителей тока ( - концентрация носителей). Каждый из носителей создает поле с индукцией
- концентрация носителей). Каждый из носителей создает поле с индукцией (18.6)
(18.6) (18.7)
(18.7) (18.8)
(18.8)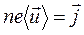 , выражение (18.8) принимает вид:
, выражение (18.8) принимает вид: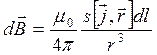 . (18.9)
. (18.9) , и считать
, и считать (18.10)
(18.10) (18.11)
(18.11) . Вывод этой формулы на основе закона Био-Савара-Лапласа изучить самостоятельно: § 42.
. Вывод этой формулы на основе закона Био-Савара-Лапласа изучить самостоятельно: § 42. и индукции магнитного поля
и индукции магнитного поля 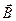 . Действительно, экспериментально установлено, что
. Действительно, экспериментально установлено, что (18.12)
(18.12) (18.13)
(18.13) (18.14)
(18.14) проводника, получаем:
проводника, получаем: (18.15)
(18.15) равно, очевидно,
равно, очевидно,  . Умножив, (18.15) на это число, получим
. Умножив, (18.15) на это число, получим (18.16)
(18.16) , а
, а  . Тогда (18.16) приводится к виду:
. Тогда (18.16) приводится к виду: (18.17)
(18.17) в магнитном поле, и выражает закон Ампера.
в магнитном поле, и выражает закон Ампера. не имеет ни начала, ни конца и всегда замкнуты. Соответственно поток
не имеет ни начала, ни конца и всегда замкнуты. Соответственно поток  (18.40)
(18.40) (18.41)
(18.41) (18.42)
(18.42) Циркуляция вектора
Циркуляция вектора  на
на 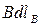 . Учтем, что
. Учтем, что 
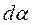 - угол, на который поворачивается радиальная прямая при перемещении вдоль контура на
- угол, на который поворачивается радиальная прямая при перемещении вдоль контура на  . Таким образом,
. Таким образом, (18.43)
(18.43)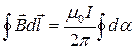 (18.44)
(18.44)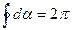 . Если же контур не охватывает тока, то
. Если же контур не охватывает тока, то  . Поэтому можно записать:
. Поэтому можно записать: (18.45)
(18.45)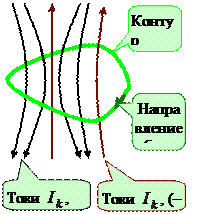 Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля
Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля  равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля
равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля  (18.46)
(18.46) (18.47)
(18.47) . Этом случае вместо
. Этом случае вместо 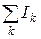 в (18.47) следует взять ток, который протекает через некоторую поверхность
в (18.47) следует взять ток, который протекает через некоторую поверхность 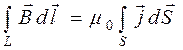 (18.48)
(18.48) . (18.49)
. (18.49) . (18.50)
. (18.50)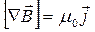 . (18.51)
. (18.51) , который называют магнитной восприимчивостью (аналогичный диэлектрической восприимчивости
, который называют магнитной восприимчивостью (аналогичный диэлектрической восприимчивости  в соотношении
в соотношении  ). Традиционно намагниченность
). Традиционно намагниченность  связывают с напряженностью магнитного поля:
связывают с напряженностью магнитного поля: . (19.17)
. (19.17)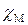 , равная произведению
, равная произведению  вещества:
вещества:  .
. . (19.18)
. (19.18) . (19.19)
. (19.19)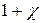 обозначают
обозначают 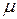 и называют относительной магнитной проницаемостью:
и называют относительной магнитной проницаемостью: . (19.20)
. (19.20) , (19.21)
, (19.21) раз меньший. Однако необходимо иметь в виду, что это утверждение перестает быть справедливым в анизотропных средах.
раз меньший. Однако необходимо иметь в виду, что это утверждение перестает быть справедливым в анизотропных средах. . Это означает, что вектор намагниченности в них направлен навстречу напряженности внешнего поля.
. Это означает, что вектор намагниченности в них направлен навстречу напряженности внешнего поля. .
. . Кроме того ферромагнетики имеют еще ряд особенностей, которые мы рассмотрим позднее. Необходимо отметить, что при повышении температуры ферромагнетики изменяют свои свойства и при характерной для каждого вещества критической температуре переходят в парамагнитное состояние, т.е. становятся парамагнетиками. Можно считать ферромагнетики частным случаем парамагнетиков, которые при понижении температуры испытывают фазовый переход в ферромагнитное состояние.
. Кроме того ферромагнетики имеют еще ряд особенностей, которые мы рассмотрим позднее. Необходимо отметить, что при повышении температуры ферромагнетики изменяют свои свойства и при характерной для каждого вещества критической температуре переходят в парамагнитное состояние, т.е. становятся парамагнетиками. Можно считать ферромагнетики частным случаем парамагнетиков, которые при понижении температуры испытывают фазовый переход в ферромагнитное состояние. оказывается эквивалентным волчку (гироскопу) и характеризуется механическим моментом импульса
оказывается эквивалентным волчку (гироскопу) и характеризуется механическим моментом импульса 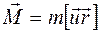 , направленным перпендикулярно плоскости орбиты и связанным с направлением движения правилом правого винта. Вращающийся по орбите электрон создает замкнутый круговой электрический ток. Направление этого тока противоположно скорости движения электрона в силу отрицательности его заряда. Величина тока определяется зарядом, переносимым электроном в единицу времени. Если частота обращения электрона равна
, направленным перпендикулярно плоскости орбиты и связанным с направлением движения правилом правого винта. Вращающийся по орбите электрон создает замкнутый круговой электрический ток. Направление этого тока противоположно скорости движения электрона в силу отрицательности его заряда. Величина тока определяется зарядом, переносимым электроном в единицу времени. Если частота обращения электрона равна  , то в единицу времени он переносит заряд
, то в единицу времени он переносит заряд  , т.е. создает ток силой
, т.е. создает ток силой  . Вектор магнитного момента
. Вектор магнитного момента 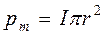 этого кругового тока связан правилом правого винта не со скоростью электрона, а с силой тока и направлен противоположно
этого кругового тока связан правилом правого винта не со скоростью электрона, а с силой тока и направлен противоположно  . Магнитный и механический моменты электрона обусловлены движением электрона по орбите и называются орбитальными.
. Магнитный и механический моменты электрона обусловлены движением электрона по орбите и называются орбитальными. (19.22)
(19.22) , (19.23)
, (19.23) , которой считают естественной единицей момента импульса. У электронов спин
, которой считают естественной единицей момента импульса. У электронов спин 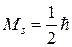 . Говорят, что электрон принадлежит к числу частиц полуцелым спином. Подставив это значение в формулу (19.23), для спинового магнитного момента электрона найдем:
. Говорят, что электрон принадлежит к числу частиц полуцелым спином. Подставив это значение в формулу (19.23), для спинового магнитного момента электрона найдем: . (19.24)
. (19.24) Разбиение кристалла на домены происходит хаотично, но таким образом, что магнитные силовые линии расположенных вблизи доменов замыкаются так, что область существования магнитного поля становится минимальной. Уменьшается и энергия, связанная с ним. Таким образом, разбиение на домены означает переход в энергетически более выгодное состояние. Идеализировано эта ситуация представлена на рисунке 19.9.
Разбиение кристалла на домены происходит хаотично, но таким образом, что магнитные силовые линии расположенных вблизи доменов замыкаются так, что область существования магнитного поля становится минимальной. Уменьшается и энергия, связанная с ним. Таким образом, разбиение на домены означает переход в энергетически более выгодное состояние. Идеализировано эта ситуация представлена на рисунке 19.9. ,
, – характерная для вещества константа Кюри-Вейсса, а
– характерная для вещества константа Кюри-Вейсса, а  – температура Кюри.
– температура Кюри. .
. . (20.10)
. (20.10)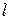 , большой по сравнению с геометрическими размерами сечения, имеющего площадь
, большой по сравнению с геометрическими размерами сечения, имеющего площадь  ). Индукция магнитного поля соленоида при силе тока в нем
). Индукция магнитного поля соленоида при силе тока в нем 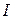
 (20.11)
(20.11)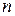 - количество витков на единицу длины соленоида;
- количество витков на единицу длины соленоида; , и через каждый из них магнитное поле создает поток
, и через каждый из них магнитное поле создает поток . (20.12)
. (20.12) . (20.13)
. (20.13) , (20.14)
, (20.14) есть объем соленоида.
есть объем соленоида.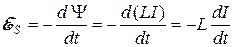 . (20.15)
. (20.15) Токи при замыкании и размыкании цепи с индуктивностью
Токи при замыкании и размыкании цепи с индуктивностью . (20.16)
. (20.16) переключатель мгновенно отключает источник тока и замыкает индуктивность на резистор. В отсутствие источника сила тока в цепи начнет убывать, но возникнет ЭДС самоиндукции, которая будет ее поддерживать. Падение напряжения на резисторе должно быть равно ЭДС самоиндукции
переключатель мгновенно отключает источник тока и замыкает индуктивность на резистор. В отсутствие источника сила тока в цепи начнет убывать, но возникнет ЭДС самоиндукции, которая будет ее поддерживать. Падение напряжения на резисторе должно быть равно ЭДС самоиндукции  :
: . (20.17)
. (20.17) :
: (20.18)
(20.18)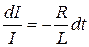 (20.19)
(20.19) . (20.20)
. (20.20) . (20.21)
. (20.21) , поэтому и константа равна этому току:
, поэтому и константа равна этому току: . (20.22)
. (20.22) Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению
Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению
 Как и самоиндукция, явление взаимной индукции является частным случаем явления электромагнитной индукции. Заключается оно в том, что если один контур создает в пространстве магнитное поле, в котором находится другой контур, то при изменениях тока в первом контуре во втором возникает ЭДС индукции (ЭДС взаимоиндукции)
Как и самоиндукция, явление взаимной индукции является частным случаем явления электромагнитной индукции. Заключается оно в том, что если один контур создает в пространстве магнитное поле, в котором находится другой контур, то при изменениях тока в первом контуре во втором возникает ЭДС индукции (ЭДС взаимоиндукции)  , которая противодействует изменению магнитного потока в первом контуре.
, которая противодействует изменению магнитного потока в первом контуре. через поверхности витков второго контура равен
через поверхности витков второго контура равен  . Этот поток, очевидно пропорционален силе тока в первом контуре:
. Этот поток, очевидно пропорционален силе тока в первом контуре: . (20.24)
. (20.24) . (20.25)
. (20.25) и
и  . (20.26)
. (20.26) Коэффициенты
Коэффициенты  и
и  называют коэффициентами взаимной индукции или взаимными индуктивностями. Их величина определяется формой, размерами, взаимным расположением контуров и магнитными свойствами окружающей среды. В отсутствие ферромагнетиков эти коэффициенты одинаковы.
называют коэффициентами взаимной индукции или взаимными индуктивностями. Их величина определяется формой, размерами, взаимным расположением контуров и магнитными свойствами окружающей среды. В отсутствие ферромагнетиков эти коэффициенты одинаковы. . При отключении источника тока магнитный поток в индуктивности должен упасть до нуля, но ЭДС самоиндукции некоторое время поддерживает ток, препятствуя его прекращению. При этом в резисторе продолжает выделяться энергия. В схеме и окружающих телах никаких изменений, кроме уменьшения индукции магнитного поля в катушке индуктивности не происходит. Остается предположить, что выделяющаяся в резисторе энергия была связана с существованием магнитного поля в катушке.
. При отключении источника тока магнитный поток в индуктивности должен упасть до нуля, но ЭДС самоиндукции некоторое время поддерживает ток, препятствуя его прекращению. При этом в резисторе продолжает выделяться энергия. В схеме и окружающих телах никаких изменений, кроме уменьшения индукции магнитного поля в катушке индуктивности не происходит. Остается предположить, что выделяющаяся в резисторе энергия была связана с существованием магнитного поля в катушке. ЭДС самоиндукции
ЭДС самоиндукции  совершает работу
совершает работу . (20.27)
. (20.27)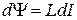 и
и . (20.28)
. (20.28) . (20.29)
. (20.29)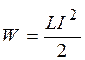 . (20.30)
. (20.30) , произведение
, произведение  дает напряженность поля соленоида, поэтому
дает напряженность поля соленоида, поэтому . (20.31)
. (20.31) . (20.32)
. (20.32) . В замкнутом контуре циркуляция этого поля дает величину ЭДС индукции:
. В замкнутом контуре циркуляция этого поля дает величину ЭДС индукции: . (20.33)
. (20.33) , можно утверждать, что
, можно утверждать, что . (20.34)
. (20.34) . (20.35)
. (20.35) . (20.36)
. (20.36)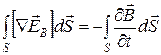 . (20.37)
. (20.37)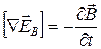 . (20.38)
. (20.38) оказался не равным нулю, в отличие от электростатического поля. Поэтому
оказался не равным нулю, в отличие от электростатического поля. Поэтому 


