
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные электрические колебания.Содержание книги Поиск на нашем сайте
В выражении для закона Ома это напряжение следует сложить с действующими в контуре напряжениями:
или
Установившиеся колебания описываются в этом случае решением уравнения (21.31), которое имеет вид:
т.е. колебания происходят на частоте вынуждающей силы. Кроме того, амплитуда колебаний заряда на конденсаторе зависит от частоты:
а между колебаниями внешнего напряжения и колебаниями заряда на конденсаторе существует сдвиг фаз: колебания заряда отстают по фазе от внешнего напряжения на угол
В случае электромагнитных колебаний, подставив в (21.33) и (21.34) значения параметров
и
Сила тока в контуре при установившихся колебаниях определяется соотношением:
где – сдвиг фаз между током и приложенным внешним напряжением.
Таким образом, знак сдвига фаз между приложенным напряжением и током в цепи определяется знаком разности Амплитуда колебаний силы тока, в соответствии с (21.37) получается умножением амплитуды колебаний заряда на
Исходное уравнение колебаний (21.30) в каждый момент времени можно представить в виде:
Слагаемые в левой части (21.41) есть напряжения на соответствующих участках цепи:
Поэтому можно сказать, что в данный момент времени сумма напряжений на элементах контура равна напряжению, приложенному извне. Падение напряжения наактивном сопротивлении R
Можно утверждать, что фазы напряжения и тока на активном сопротивлении совпадают. Напряжение на ёмкости
Сравнивая это соотношение с (21.43), видим, что напряжение на ёмкости отстаёт по фазе от силы тока на Максимальное значение (амплитудное)
.Однако в соответствии с (21.40)
Напряжение на индуктивности
Причём Следовательно на индуктивности напряжение опережает ток на
Величину и сопротивление проводников называют активным.
При измерении частоты вынуждающего генератора изменяется амплитудное значение заряда При частоте
Резонансные кривые для тока имеют несколько иной вид. Из выражения
 . Следовательно, резонансная частота, для тока совпадает с собственной частотой контура . Следовательно, резонансная частота, для тока совпадает с собственной частотой контура  . На фазовой диаграмме при . На фазовой диаграмме при  векторы, соответствующие напряжениям на индуктивности и ёмкости оказываются равными противоположено направленными. Соответственно сопротивление контура оказывается чисто активным и минимальным. Течёт максимальный ток. Кроме того, при переходе через векторы, соответствующие напряжениям на индуктивности и ёмкости оказываются равными противоположено направленными. Соответственно сопротивление контура оказывается чисто активным и минимальным. Течёт максимальный ток. Кроме того, при переходе через  сдвиг фаз между током в контуре и п риложенным внешним напряжением меняет знак. сдвиг фаз между током в контуре и п риложенным внешним напряжением меняет знак.
По этой причине в радиотехнике резонансом называют такой режим работы электрической цепи, содержащей индуктивности и ёмкости, при котором реактивная составляющая сопротивления (или проводимости) цепи равна нулю. Такой резонанс называют фазовым.
Таким образом на резонансной частоте сопротивление и проводимость электрической цепи имеют чисто активный характер, фазы тока и приложенные напряжения совпадают. Рассмотренный нами случай, когда внешнее напряжение и элементы цепи включены последовательно, наз. последовательным резонансным контуром. В таком контуре при резонансе (фазовом!) напряжение на ёмкости равно по амплитуде напряжению на индуктивности
но эти напряжения противофазны и компенсируют друг друга. Внешнее напряжение равно напряжению на активном сопротивлении и совпадает по фазе с током. Такая разновидность резонанса называется резонансомнапряжений. В резонансе амплитуда тока
При этом напряжение на конденсаторе
На рис. показан параллельный резонансный контур, к точками a и b которого приложено переменное напряжение
В отличие от последовательного контура, в котором общим является ток во всех элементах, и рассматривается сложением колебаний напряжения, в этом случае общим является напряжение
тока. Построим векторную диаграмму токов. Пусть вектор внешнего напряжения будет горизонтальным. Амплитуда тока через индуктивность.
(замена конденсатора означает переход к
Вектор тока через ёмкость имеет амплитуду
и опережает напряжение на При резонансе: результирующий ток совпадает по фазе с U и контур ведёт себя как чисто активное сопротивление. Этой ситуации соответствует следующая векторная диаграмма:
минимальное значение результирующего тока, следовательно сопротивление контура становится максимальным. Если сопротивление катушки стремится к нулю, то Рассмотренный случай называется резонансом токов.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.01 с.) |

 Вынeужденные колебания можно осуществить, например, включив последовательно с элементами контура переменную ЭДС:
Вынeужденные колебания можно осуществить, например, включив последовательно с элементами контура переменную ЭДС: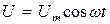 (21.28)
(21.28) (21.30)
(21.30)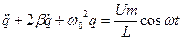 (21.31)
(21.31) , (21.32)
, (21.32) , (21.33)
, (21.33) , который определяется соотношением:
, который определяется соотношением: . (21.34)
. (21.34) , получим соотношения:
, получим соотношения: . (21.35)
. (21.35) . (21.36)
. (21.36) . (21.37)
. (21.37) (21.38)
(21.38) . (21.39)
. (21.39) .
. и определяется соотношением:
и определяется соотношением: . (21.40)
. (21.40) . (21.41)
. (21.41) (21.42)
(21.42) . (21.43)
. (21.43) получим, разделив выражение для заряда на его емкость
получим, разделив выражение для заряда на его емкость 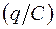 :
: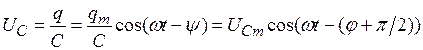 (21.44)
(21.44) . (21.45)
. (21.45) .
. . (21.45)
. (21.45) . Поэтому можно утверждать, что амплитудное значение напряжение на конденсаторе и амплитуда тока в контуре связаны простым соотношением:
. Поэтому можно утверждать, что амплитудное значение напряжение на конденсаторе и амплитуда тока в контуре связаны простым соотношением: . (21.46)
. (21.46) . (21.47)
. (21.47) . (21.48)
. (21.48) .
. называют ёмкостным сопротивлением, в силу того, что в соотношении (21.46) эта величина является коэффициентом пропорциональности между амплитудой напряжения и силой тока в контуре. Величину
называют ёмкостным сопротивлением, в силу того, что в соотношении (21.46) эта величина является коэффициентом пропорциональности между амплитудой напряжения и силой тока в контуре. Величину 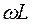 по аналогии называют индуктивным сопротивлением. Индуктивное и ёмкостное сопротивления называют реактивными сопротивлениями, подчеркивая тот факт, что на этих сопротивлениях не происходит преобразования электромагнитной энергии в тепловую. В отличии от этого на обычном резисторе, в соответствии с законом Джоудя – Ленца такое преобразование происходит,
по аналогии называют индуктивным сопротивлением. Индуктивное и ёмкостное сопротивления называют реактивными сопротивлениями, подчеркивая тот факт, что на этих сопротивлениях не происходит преобразования электромагнитной энергии в тепловую. В отличии от этого на обычном резисторе, в соответствии с законом Джоудя – Ленца такое преобразование происходит,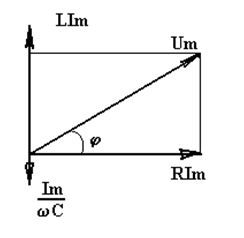 Эти фазовые соотношения удобно отобразить на векторной диаграмме, отражающей тот факт, что сумма напряжений на элементах контура равна действующей внешней ЭДС.
Эти фазовые соотношения удобно отобразить на векторной диаграмме, отражающей тот факт, что сумма напряжений на элементах контура равна действующей внешней ЭДС. и, соответственно, амплитуда напряжения на ёмкости
и, соответственно, амплитуда напряжения на ёмкости  .
.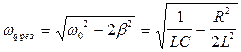 . (21.47)
. (21.47)
 и
и  достигают максимума. Это явление соответствует резонансу в механике. Заряд играет в электрических колебаниях ролькоординаты. Примерный вид зависимостей амплитудного значения заряда конденсатора (а значит и напряжения на конденсаторе) от частоты внешнего напряжения показан на рисунке. Важно отметить, что кривые не выходят из начала координат. Это означает, что при приложении к контуру постоянного напряжения его заряд имеет некоторое конечное значение. В соответствии с (21.47) резонансная частота уменьшается по мере увеличения активного сопротивления в контуре.
достигают максимума. Это явление соответствует резонансу в механике. Заряд играет в электрических колебаниях ролькоординаты. Примерный вид зависимостей амплитудного значения заряда конденсатора (а значит и напряжения на конденсаторе) от частоты внешнего напряжения показан на рисунке. Важно отметить, что кривые не выходят из начала координат. Это означает, что при приложении к контуру постоянного напряжения его заряд имеет некоторое конечное значение. В соответствии с (21.47) резонансная частота уменьшается по мере увеличения активного сопротивления в контуре.
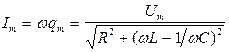


 . (21.47)
. (21.47) . (21.47)
. (21.47)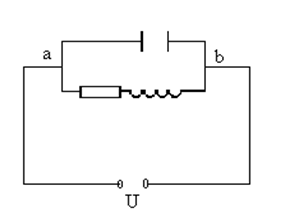 Таким образом, при резонансе напряжений напряжение на конденсаторе в Q раз превосходит напряжение внешнего источника.
Таким образом, при резонансе напряжений напряжение на конденсаторе в Q раз превосходит напряжение внешнего источника.
 , а сила тока в ветвях различна:
, а сила тока в ветвях различна: . (21.47)
. (21.47) Поэтому задача сводится к сложению колебаний
Поэтому задача сводится к сложению колебаний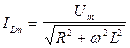
 )
)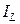 сдвинут (отстаёт) по фазе относительно оси напряжений на угол
сдвинут (отстаёт) по фазе относительно оси напряжений на угол  ,
,
 (43)
(43)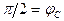
 Очевидно, что резонансу соответствует
Очевидно, что резонансу соответствует стремится к
стремится к  и при резонансе с нулевым R токи в индуктивности и ёмкости полностью компенсируют друг друга. При этом ток в подводящих проводах был бы равен нулю, хотя
и при резонансе с нулевым R токи в индуктивности и ёмкости полностью компенсируют друг друга. При этом ток в подводящих проводах был бы равен нулю, хотя  ,
,  могли бы быть достаточно большими. При этом сопротивление контура
могли бы быть достаточно большими. При этом сопротивление контура  .
.


