
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа при перемещении тока в магнитном полеСодержание книги Поиск на нашем сайте
Рассмотрим контур с током, в котором одна сторона подвижна и имеет длину l. При показанных на рисунке направлениях тока и индукции на подвижную сторону действует сила
Величину При конечно перемещении участка контура
где Ф1 и Ф2 - начальное и конечное значения магнитного потока через контур. Можно показать, что формула (18.39) справедлива и в общем случае при произвольном перемещении любого контура в однородном и неоднородном магнитном поле. Дивергенция магнитного поля До настоящего времени экспериментально обнаружить магнитные заряды не удалось. Соответственно линии вектора
– поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Преобразуем поверхностный интеграл в (18.40) по теореме Остроградского-Гаусса:
Уравнение (18.41) должно выполняться для произвольного объема, а поэтому
Соотношение (18.42)выражает теорему Гаусса в дифференциальной форме для вектора индукции магнитного поля. Ротор магнитного поля
Тогда для циркуляции получаем
Если рассматриваемый контур охватывает ток, то при обходе по контуру радиальная прямая поворачивается в одном направлении и
где под I подразумевается ток, охватываемый контуром. В выражении (18.45) ток рассматривается как алгебраическая величина: если направление обхода контура образует с направлением тока правовинтовую систему, то ток считают положительным, в противном случае - отрицательным. Формула (18.45) получена для прямого тока. Но можно доказать, что онасправедлива и в общем случае, для тока произвольной формы.
По формуле (18.45)
Важно помнить, что сумма в (18.47) является алгебраической. Возможны ситуации, когда токи распределены в пространстве с некоторой плотностью
По теореме Стокса
Следовательно
Поверхность интегрирования может быть произвольной (опирающуйся на контур L), поэтому должны быть равны подынтегральные выражения:
Формулы (18.48) и (18.51) отражают существенное отличие электрического и магнитного полей: циркуляция и ротор вектора напряженности электрического поля равны нулю. Это является следствием того, что электростатическое поле потенциально и может быть описано с помощью скалярного потенциала. Магнитное поле не является потенциальным, его циркуляция не обязательно равна нулю, его нельзя описать с помощью скалярного потенциала. Такие поля называют вихревыми или соленоидальными. Поле соленоида и тороида. Самостоятельно. Обратить внимание на вид силовых линий этих полей и формулы для индукции. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.006 с.) |

 , которая, при перемещении перемычки на расстояние
, которая, при перемещении перемычки на расстояние  совершит работу
совершит работу (18.38)
(18.38) следует понимать как поток через площадь, описанную перемычкой при её движении. Соответственно работа, совершаемая магнитной силой при перемещении участка контура с током, равна произведению силы тока на величину магнитного потока, через поверхность, описанную участком при перемещении.
следует понимать как поток через площадь, описанную перемычкой при её движении. Соответственно работа, совершаемая магнитной силой при перемещении участка контура с током, равна произведению силы тока на величину магнитного потока, через поверхность, описанную участком при перемещении.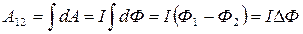 (18.39)
(18.39) не имеет ни начала, ни конца и всегда замкнуты. Соответственно поток
не имеет ни начала, ни конца и всегда замкнуты. Соответственно поток  (18.40)
(18.40) (18.41)
(18.41) (18.42)
(18.42) Циркуляция вектора
Циркуляция вектора  на
на 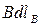 . Учтем, что
. Учтем, что 
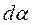 - угол, на который поворачивается радиальная прямая при перемещении вдоль контура на
- угол, на который поворачивается радиальная прямая при перемещении вдоль контура на  . Таким образом,
. Таким образом, (18.43)
(18.43)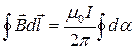 (18.44)
(18.44)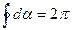 . Если же контур не охватывает тока, то
. Если же контур не охватывает тока, то  . Поэтому можно записать:
. Поэтому можно записать: (18.45)
(18.45)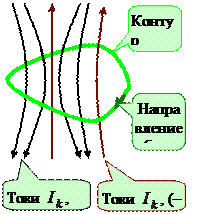 Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля
Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля  равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля
равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля  (18.46)
(18.46) (18.47)
(18.47) . Этом случае вместо
. Этом случае вместо 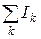 в (18.47) следует взять ток, который протекает через некоторую поверхность
в (18.47) следует взять ток, который протекает через некоторую поверхность 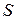 , опирающуюся на контур L. При этом поверхность может быть произвольной, единственное требование – она должна опираться на контур L. Суммарный ток через такую поверхность равен потоку вектора
, опирающуюся на контур L. При этом поверхность может быть произвольной, единственное требование – она должна опираться на контур L. Суммарный ток через такую поверхность равен потоку вектора 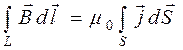 (18.48)
(18.48) . (18.49)
. (18.49) . (18.50)
. (18.50)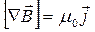 . (18.51)
. (18.51)


