
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контур без активного сопротивления.Содержание книги Поиск на нашем сайте
Закон Ома и правила Кирхгофа установлены и, строго говоря, справедливы для постоянного тока. Однако, они остаются практически справедливыми и для мгновенных значений изменяющихся токов и напряжений, если их изменения происходят не слишком быстро. Если за время t, распространения электромагнитного возмущения по длине l всей цепи, сила тока изменяется незначительно, то такие токи называются квазистационарными. Математически для периодически изменяющихся токов условие квазистационарности имеет вид:
Т - период. Для квазистационарных токов закон Ома справедлив и мы будем рассматривать только такие токи.
Например, рассмотрим процессы при замыкании заряженного конденсатора на катушку индуктивности. Будем считать, что сопротивление проводников схемы равно нулю. 1. 2. Однако ток в цепи не прекращается, вследствие того, что ЭДС самоиндукции изменяет знак на противоположный и поддерживает его. Протекая в прежнем направлении, ток начинает заряжать конденсатор, но полярность зарядов на обкладках конденсатора меняется на противоположную. Энергия системы начинает преобразовываться из энергии магнитного поля в энергию электрического поля конденсатора. Процесс подзарядки конденсатора продолжается до полного перехода энергии в поле конденсатора. Напряжение на конденсаторе достигает максимального значения, равного исходному, но имеет противоположную полярность. По времени описанные процессы составляют вторую четверть периода электромагнитного колебания в контуре. 3. В третьей четверти периода процессы в контуре повторяют первую, но начинаются с заряженного состояния конденсатора, отличающегося обратной полярностью. 4. В четвертой четверти процессы аналогичны второй, но конденсатор и система возвращаются в исходное состояние. Найдём уравнение колебаний в таком контуре. Условимся считать положительным ток, заряжающий конденсатор:
Подставим в (21.03) выражения для ЭДС и учтем, что по предположению в контуре нет активного сопротивления:
Но по определению силы тока
Поэтому уравнению (21.04) можно придать вид:
Уравнение точно такого вида мы решали при рассмотрении механических колебаний. Положив
Решение (21.07) имеет вид
Период колебаний определяется по формуле Томпсона
Напряжение на конденсаторе изменяется по закону:
Дифференцируя (21.08) по времени, найдём для силы тока:
Сравнивая (21.10)и (21.11), видим, что сила тока опережает по фазе напряжение на конденсаторе на p/2. Когда ток достигает максимума, напряжение обращается в нуль и наоборот. С учетом именно этого утверждения построены графики на рисунке 1. Представляет интерес рассмотреть отношение максимального напряжения на конденсаторе
следовательно,
Затухающие колебания. Во всяком реальном контуре обязательно присутствует активное сопротивление R. Соответственно выражение для закона Ома будет иметь вид (21.03):
Разделим (21.14) на
Получаем дифференциальное уравнение, описывающее колебания в контуре с ненулевым активным сопротивлением:
Параметр Решение (21.16) при не слишком большом затухании имеет вид (как известно!):
«…при не слишком большом затухании» означает:
В этом случае циклическая частота колебаний остается вещественной:
Из (21.19) следует, что частота затухающих (т.е. при ненулевом сопротивлении в контуре) колебаний меньше собственной. Для характеристики степени затухания колебаний используют логарифмический декремент затухания, который определяется соотношением:
Напомним, что В нашем случае
поскольку При небольшом затухании
Чаще для характеристики степени затухания колебаний используется добротность контура:
Добротность контура, как и любой колебательной системы, пропорциональна Энергия, запасённая в контуре, пропорциональна квадрату напряжения на конденсаторе, а значит, уменьшается по закону:
Тогда отношение энергии DW, теряемой в контуре за период к запасённой Если (!) затухание невелико: l << 1, то
Другими словами добротность пропорциональна отношению энергии запасённой в контуре к энергии, теряемой за период.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.006 с.) |

 (21.01)
(21.01) Простейшей цепью, в которой могут возникнуть электрические колебания, является цепь, состоящая из ёмкости С и индуктивности L. Колебания в контуре можно вызвать либо сообщив конденсатору начальный заряд, либо возбудив в индуктивности индукционный ток, например, выключив внешнее магнитное поле.
Простейшей цепью, в которой могут возникнуть электрические колебания, является цепь, состоящая из ёмкости С и индуктивности L. Колебания в контуре можно вызвать либо сообщив конденсатору начальный заряд, либо возбудив в индуктивности индукционный ток, например, выключив внешнее магнитное поле.
 В начальный момент времени энергия системы сосредоточена в электрическом поле конденсатора. При замыкании цепи в цепи возникает электрический ток, возбуждающий в катушке нарастающее магнитное поле, с которым оказывается связанной часть запасенной конденсатором энергии. В катушке возбуждается ЭДС самоиндукции, которая противодействует нарастанию тока, в соответствии с правилом Ленца. Ток продолжает нарастать (энергия переходит в энергию магнитного поля катушки) и достигает максимального значения при полном разряде конденсатора. При этом изменение тока прекращается, ЭДС самоиндукции обращается в нуль. Вся запасенная конденсатором энергии преобразуется в энергию магнитного поля в катушке индуктивности. По времени описанные процессы составляют четверть периода электромагнитного колебания в контуре.
В начальный момент времени энергия системы сосредоточена в электрическом поле конденсатора. При замыкании цепи в цепи возникает электрический ток, возбуждающий в катушке нарастающее магнитное поле, с которым оказывается связанной часть запасенной конденсатором энергии. В катушке возбуждается ЭДС самоиндукции, которая противодействует нарастанию тока, в соответствии с правилом Ленца. Ток продолжает нарастать (энергия переходит в энергию магнитного поля катушки) и достигает максимального значения при полном разряде конденсатора. При этом изменение тока прекращается, ЭДС самоиндукции обращается в нуль. Вся запасенная конденсатором энергии преобразуется в энергию магнитного поля в катушке индуктивности. По времени описанные процессы составляют четверть периода электромагнитного колебания в контуре.
 . (21.02)
. (21.02)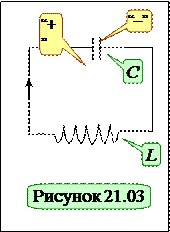 Тогда по второму правилу Кирхгофа падение напряжения на активном сопротивлении цепи должно быть равно сумме ЭДС, действующих в контуре. В контуре имеется конденсатор, напряжение, на котором
Тогда по второму правилу Кирхгофа падение напряжения на активном сопротивлении цепи должно быть равно сумме ЭДС, действующих в контуре. В контуре имеется конденсатор, напряжение, на котором  можно рассматривать, как ЭДС, которую следует взять в сумме «с минусом», поскольку она напрвлена навстречу току зарядки конденсатора. К этой ЭДС необходимо добавить ЭДС самоиндукции
можно рассматривать, как ЭДС, которую следует взять в сумме «с минусом», поскольку она напрвлена навстречу току зарядки конденсатора. К этой ЭДС необходимо добавить ЭДС самоиндукции  . Поэтому уравнение по второму правилу Кирхгофа следует записать в виде:
. Поэтому уравнение по второму правилу Кирхгофа следует записать в виде: (21.03)
(21.03)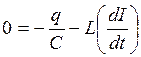 . (21.04)
. (21.04) . (21.05)
. (21.05) . (21.06)
. (21.06) , получим
, получим . (21.07)
. (21.07) . (21.08)
. (21.08) называется: собственной частотой контура.
называется: собственной частотой контура. . (21.09)
. (21.09) . (21.10)
. (21.10)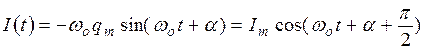 . (21.11)
. (21.11) к максимальному току
к максимальному току  . Это отношение имеет размерность сопротивления и называется характеристическим сопротивлением контура. Поскольку
. Это отношение имеет размерность сопротивления и называется характеристическим сопротивлением контура. Поскольку  , а
, а  , то
, то . (21.12)
. (21.12) . (21.13)
. (21.13) или
или  . (21.14)
. (21.14) и воспользуемся обозначением:
и воспользуемся обозначением: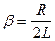 . (21.15)
. (21.15) (21.16)
(21.16) называется коэффициентом затухания. По смыслу эта величина обратна времени, в течение которого амплитуда колебаний уменьшается в «е» раз.
называется коэффициентом затухания. По смыслу эта величина обратна времени, в течение которого амплитуда колебаний уменьшается в «е» раз. (21.17)
(21.17) . (21.18)
. (21.18) . (21.19)
. (21.19) . (21.20)
. (21.20)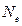 есть количество колебаний, совершаемых системой за время, пока амплитуда колебаний уменьшается в «е» раз.
есть количество колебаний, совершаемых системой за время, пока амплитуда колебаний уменьшается в «е» раз. и
и  , поэтому
, поэтому . (21.21)
. (21.21) определяется параметрами контура
определяется параметрами контура  , то логарифмический декремент затухания l является характеристикой контура. Важно отметить, что соотношение (21.21) справедливо всегда, в отличии от широко используемого приближенного соотношения, которое мы сейчас рассмотрим.
, то логарифмический декремент затухания l является характеристикой контура. Важно отметить, что соотношение (21.21) справедливо всегда, в отличии от широко используемого приближенного соотношения, которое мы сейчас рассмотрим. ,и вторым слагаемым в (21.19) можно пренебречь. Тогда
,и вторым слагаемым в (21.19) можно пренебречь. Тогда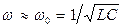 . (21.22)
. (21.22) . (21.23)
. (21.23) . (21.24)
. (21.24) .
. . (21.25)
. (21.25) . (21.26)
. (21.26) , а значит
, а значит . (21.27)Отсюда находим, что
. (21.27)Отсюда находим, что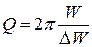 . (21.27)
. (21.27)


