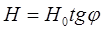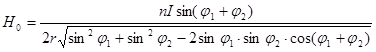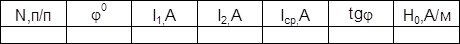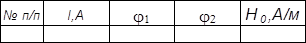Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение магнитного поля Земли.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задание: определить горизонтальную составляющую напряженности магнитного поля Земли с помощью тангенс-буссоли.
Принадлежности: тангенс-буссоль, источник питания, переключатель, цифровой вольтметр. ТЕОРИЯ ВОПРОСА. Элементы земного магнетизма. Земля представляет собой естественный магнит, магнитные полюса которого располагаются недалеко (300 км) от географических. Причём северный геомагнитный полюс расположен на Юге, в Антарктиде. Через магнитные полюса Земли можно провести линии больших кругов – магнитные меридианы, перпендикулярно к ним – линию большого круга – магнитный экватор – и параллельно последнему - линию малых кругов – магнитные параллели. Таким образом, каждой точке на Земле будет соответствовать не только географические, но и магнитные координаты. Из-за несовпадения магнитных и географических полюсов Земли не совпадают и плоскости магнитного и географического меридианов, проходящих через данную точку на земной поверхности. Положение свободно расположенной магнитной стрелки характеризуется двумя углами a и b, определёнными для данной точки Земли. Магнитное склонение a - это угол между направлениями географического и магнитного меридиана, а магнитное наклонение b - это угол между направлением напряжённости поля в данной точке и горизонтальной плоскостью. Эти два угла – склонение и наклонение – называются элементами земного магнетизма. Магнитное поле Земли подвержено суточным, годовым, вековым колебаниям. Соответственно меняются и элементы земного магнетизма. Кроме того, наблюдаются кратковременные нерегулярные отклонения – так называемые магнитные бури, появление которых связано с деятельностью Солнца, в частности с числом солнечных пятен. Нужно отметить, что магнитная стрелка или рамка с током устанавливается в определённом направлении под действием вектора индукции
Рис.1.
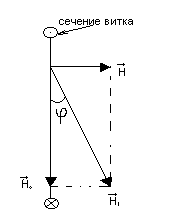
Определение горизонтальной составляющей напряженности магнитного поля Земли На рис.2 изображено сечение катушки горизонтальной плоскостью. Здесь
Рис.2.
Тогда получим С другой стороны, напряженность магнитного поля в центре катушки тангенс-буссоли, исходя из закона Био-Савара-Лапласа, может быть определена по формуле: Н = n I/ 2r, где I – ток, r - радиус витков буссоли (r=25 см), n – число витков(n = 32). Тогда nI / 2r = H0 tg j; H0 = n I. / 2r tg j (1)
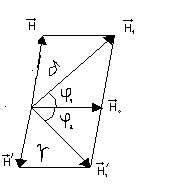
В общем случае тангенс-буссоль может быть ориентирована произвольно, тем более, что точная установка ее в направлении магнитного меридиана затруднительна. Тогда величину Н0 можно определить, переключая направление тока и записывая углы поворота стрелки компаса j1 и j 2 от начального значения. Действительно, из рис.3 видно, что в этом случае
Рис.3.
j 1 + j2 + d + g = p Н /sin j 2=Н0 /sin g; H / sin j1 = H 0 /sin d
Решением полученной системы является:
(2)
При j1 = j2 = j эта формула превращается в формулу (1).
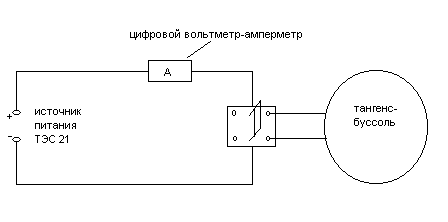
Электрическая схема установки изображена на рис. 4.
Рис. 4.
Порядок выполнения работы. Упражнение 1. 1.Установить тангенс-буссоль в плоскости магнитного меридиана Земли (по магнитной стрелке). 2.Собрать схему и подключить установку к источнику питания. Замкнуть переключатель и установить с помощью источника питания такой ток, чтобы угол поворота магнитной стрелки был равным 450. Записать значение силы тока по миллиамперметру I 1. 3.Переключателем изменить направление тока в буссоли и записать новое отклонение стрелки I 2 (перемена направления тока позволяет избавиться от ошибки, создаваемой неточным совпадением плоскости тангенс-буссоли с плоскостью магнитного меридиана). Повторить измерения несколько раз. Для расчета взять среднее арифметическое значение тока Icp. = (I1+I2)/2. Рассчитать Н0 по формуле (1).
4.Такие измерения произвести при 4-5 других значениях силы тока, так чтобы j = 300, 350, 400, 500, 55 0, 60 0 Данные занести в таблицу 1.
Таблица 1.
Упражнение 2. Определение значения Н0 при произвольной ориентации тангенс-буссоли. 1.Сориентировать плоскость тангенс-буссоли так, чтобы угол между нормалью к плоскости и магнитной стрелкой был отличен от 0 и 900. 2.Нулевое значение угла компаса совместить с направлением Н0. 3.Пропустить по виткам тангенс-буссоли определённый ток. 4.Определить углы поворота стрелки компаса j 1 и j2, переключая направление тока в буссоли. 5.Рассчитать значение Н0 по формуле (2). Измерения повторить три раза. Данные занести в таблицу 2.
Таблица 2.
6.Сравнить значения Н0, полученные в двух упражнениях.
КОНТРОЛЬНЫЕ ВОПРОСЫ: 1.Закон Био-Савара-Лапласа. Вектор индукции и напряженности магнитного поля. Как определяется направление dB? 2. Силовые линии магнитного поля. Поле кругового проводника с током. Вывести формулу для индукции магнитного поля в центре. Как направлен вектор В? 3. Метод определения горизонтальной составляющей напряженности магнитного поля Земли с помощью тангенс-буссоли. 4. Почему магнитная стрелка тангенс-буссоли должна быть малых размеров?
Литература: 1. ЧечкинС.А. Основы геофизики,- Л., Гидрометеоиздат,1990; 2. Дж. Д. Макдугалл. Краткая история планеты Земля, Санкт-Петербург, 2001; Трофимова Т.И. Курс физики. -М., Высшая школа, 1997.
Лабораторная работа № 9.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 968; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.007 с.) |

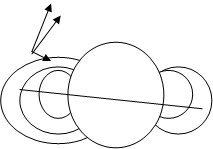
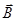 магнитного поля, а не вектора напряжённости
магнитного поля, а не вектора напряжённости 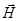 . Но так как воздух представляет собой изотропную среду,
. Но так как воздух представляет собой изотропную среду, 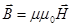 и направления
и направления 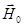 и вертикальную
и вертикальную 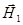 составляющие (рис.1). Значит, магнитная стрелка, вращающаяся на закреплённой вертикальной оси (компас), будет останавливаться в плоскости магнитного меридиана под действием именно горизонтальной составляющей магнитного поля Земли. Если с помощью кругового тока около стрелки создать ещё одно магнитное поле, то она установится по направлению равнодействующей напряженности обоих магнитных полей. Так как поле кругового тока нетрудно вычислить, зная величину тока, протекающего в витке, и радиус витка, то величину горизонтальной составляющей вектора напряжённости магнитного поля Земли
составляющие (рис.1). Значит, магнитная стрелка, вращающаяся на закреплённой вертикальной оси (компас), будет останавливаться в плоскости магнитного меридиана под действием именно горизонтальной составляющей магнитного поля Земли. Если с помощью кругового тока около стрелки создать ещё одно магнитное поле, то она установится по направлению равнодействующей напряженности обоих магнитных полей. Так как поле кругового тока нетрудно вычислить, зная величину тока, протекающего в витке, и радиус витка, то величину горизонтальной составляющей вектора напряжённости магнитного поля Земли 
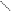
 H0 H
H0 H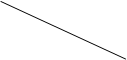
 H1
H1