
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Между эффективными значениями тока и напряжения существует связьСодержание книги
Поиск на нашем сайте
Iэф.= Uэф/Z (3) Величина Z называется полным сопротивлением цепи. Выражение (3) есть закон Ома для цепи переменного тока. 1.Сопротивление в цепи переменного тока. Рассмотрим случай, когда источник переменного тока замкнут на внешнюю цепь, имеющую настолько малые индуктивность и емкость, что ими можно пренебречь. В цепи имеется переменный ток I= I0 sin wt. Найдем, по какому закону изменяется напряжение между точками а и б (рис.1). Применяя закон Ома, имеем U= I R= I0 R sin wt.
~U V R
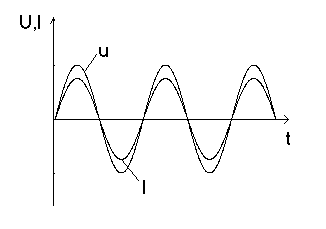
б Рис.1 Таким образом, напряжение на концах участка цепи изменяется также по закону синусов, причем разность фаз между колебаниями тока и напряжения равна нулю. Напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль (рис.2). Максимальное значение напряжения U0= I0 R.
Рис.2 Гармонически изменяющиеся величины удобно наглядно изображать при помощи векторных диаграмм. Выберем ось диаграммы так, чтобы вектор, изображающий колебания тока, был направлен вдоль оси токов. Тогда вектор напряжения будет также направлен вдоль оси токов, так как разность фаз между током и напряжением равна нулю (рис.3). Длина этого вектора равна амплитуде напряжения U0= I0 R.
Рис.3 2. Ёмкость в цепи переменного тока. Пусть участок цепи содержит конденсатор ёмкостью С, причём сопротивлением и индуктивностью участка можно пренебречь (рис.4).
V
A
С Рис.4 Емкость конденсатора измеряется зарядом, находящимся на каждой из обкладок, если напряжение между обкладками равно единице, тогда С= q/U. Единицей емкости в системе СИ служит фарада (Ф). 1Ф= 1 Кл/В. Емкость конденсатора зависит от его размеров, формы и диэлектрической проницаемости среды, разделяющей обкладки. Если сила тока в цепи изменяется по закону I= I0 sin wt (4) то из I= dq/dt следует, что q= ò I0 sin wt dt = - I0/w * cos wt + q0. Положим q0 =0. Следовательно, U= - I0 / wC *cos wt = I0 / wC *sin (wt -p/2) (5) Сравнивая (4) и (5), мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону синуса, но колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2 (рис.5).
Рис.5 Напряжение на конденсаторе в какой-то момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебания. Поэтому колебания напряжения запаздывают относительно колебаний тока. Пусть в момент t=0 сила тока равна нулю, но на конденсаторе ещё имеется отрицательный заряд, перенесенный током в предыдущий период времени, и напряжение не равно нулю. Для обращения в нуль этого заряда необходимо, чтобы некоторое время t проходил ток положительного направления, и поэтому, когда заряд конденсатора (а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю.
Из формулы (5) амплитуда колебаний напряжения на конденсаторе равна U0= I0/wС. Cравнивая это выражение с законом Ома для участка цепи с постоянным током (U= I R), мы видим, что величина Zc= 1/wС представляет собой сопротивление конденсатора для переменного тока, т.е. емкостное сопротивление. Оно обратно пропорционально круговой частоте тока и величине емкости. Чем больше емкость конденсатора и чем чаще изменяется направление тока (т.е. чем больше круговая частота w), тем больший заряд проходит за единицу времени через поперечное сечение подводящих проводов. Следовательно, I ~ wС. Но сила тока и сопротивление обратно пропорциональны друг другу, тогда сопротивление Zc ~ 1/wС.
-p/2 U0= I0/wС Рис.6 Полученные результаты представим в виде векторной диаграммы (рис.6). Здесь вектор, изображающий колебания напряжения, повернут относительно оси токов в отрицательном направлении (по часовой стрелке) на угол p/2. Длина этого вектора равна амплитуде напряжения U0= I0/wС. 3. Индуктивность в цепи переменного тока. Рассмотрим случай, когда участок цепи содержит только индуктивность (рис.7).
Рис.7 При наличии переменного тока в катушке индуктивности возникает э.д.с. самоиндукции e, и поэтому мы видим, что, применив Закон Ома для участка цепи с э.д.с., получим: U= I r - e. При r®0 (омическое сопротивление цепи пренебрежимо мало) и e= -L×dI/dt будем иметь U= L×dI/dt. Если сила тока в цепи изменяется по закону синуса I= I0 sin wt (6) то U= I0 wL cos wt= = I0 wL sin (wt + p/2) (7) Сравнивая (6) и (7), видим, что колебания напряжения на индуктивности опережают по фазе колебания тока на p/2. Когда сила тока, возрастая, проходит через нуль, напряжение уже достигает максимума, после чего начинает уменьшаться; когда сила тока становится максимальной, напряжение проходит через нуль и т.д. (рис.8).
Рис. 8 Индуктивность контура равна связанному с ним магнитному потоку, если в контуре идет ток, равный единице (L= Ф/I). Единицей индуктивности в системе СИ служит Генри (1 Гн= 1 Вб/А). Индуктивность зависит от формы и размеров контура и от магнитной проницаемости среды. Сдвиг фаз обусловлен тормозящим действием электродвижущей силы самоиндукции: она препятствует как нарастанию, так и убыванию тока в цепи, поэтому максимум тока наступает позднее, чем максимум напряжения. Наличие омического сопротивления привело бы к уменьшению сдвига фаз. Из (7) следует, что амплитуда напряжения равна U0= I0 wL и, следовательно, величина ZL=wL играет ту же роль, что и сопротивление участка. Она представляет собой индуктивное сопротивление катушки. Оно пропорционально круговой частоте тока и величине индуктивности. Эта зависимость объясняется тем, что индуктивное сопротивление обусловлено действием электродвижущей силы самоиндукции, уменьшающей эффективный ток и, следовательно, увеличивающей сопротивление. Величина же этой э.д.с. (следовательно, сопротивления) пропорциональна индуктивности катушки L и скорости изменения тока, т.е. круговой частоте w.
P/2 О I Рис. 9 Полученные результаты представим на векторной диаграмме (рис.9). Вектор, изображающий колебания напряжения, повернут относительно оси токов в положительном направлении (против часовой стрелки) на угол p/2, а его длина равная амплитуде есть I0 wL. 4. Закон Ома для переменных токов.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.102.152 (0.01 с.) |

 А а
А а

 0 U0= I0 R
0 U0= I0 R
 ось токов
ось токов ~U
~U




 а б
а б



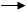 I
I
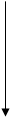
 О I
О I

 ~U
~U





 L A
L A I
I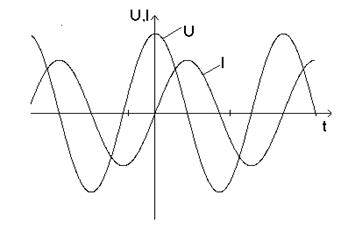

 U0=I0 wL
U0=I0 wL


