
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле. Индукция и напряженность магнитного поля. Закон ампера.
Проводники с током в магнитном поле. Взаимодействие параллельных токов. Если в поле (или электромагнита) поместить проводник с током, который создает свое собственное магнитное поле, то оба магнитных поля, взаимодействуя между собой, создадут силу, которая стремиться вытолкнуть проводник из поля. Как видно на рисунке №1 А, магнитные силовые линии поля и проводника слева от него совпадают по направлению и их полностью здесь больше, чем справа от проводника где магнитные силовые линии проводника идут навстречу линиям поля и ослабляют одна другую. Проводник выталкивается из магнитного поля вправо. Если изменить направление тока в проводнике (рисунок №1 Б), то направление силы также изменится. Сила с которой поле действует на проводник, Для определения направления силы, действующей в магнитном поле, применяют правило левой руки: если расположить левую руку так, чтобы магнитные линии входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока проводнике, то большой палец укажет направление действия силы, приложенной к проводнику. Два параллельных тока одинакового направления притягиваются друг к другу с силой, равной
Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением. Движение заряженной частицы в магнитном поле. Сила Лоренца. Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях. Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и В равен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила Лоренца F =Q[ vB ] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv2/r, следовательно
Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,
Подствавив(1),получим т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц. Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q - заряд частицы;
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0, и заряд в магнитном поле движется равномерно и прямолинейно. Магнитное поле. Индукция и напряженность магнитного поля. Закон Ампера. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. Магнитное поле может создаваться током заряженных частиц и/или магнитным моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля Магни́тная инду́кция Более конкретно, Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. В СИ: Зако́н Ампе́ра — закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. dF=I{dI,B} B-вектор магнитной индукции, dI-вектор по модулю равный и совпадающий с током, dF направление определяется по правилу левой руки (Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.) 2) Закон Био - Савара-Лапласа и следствия из него: после прямого тока и в центре кругового тока. Это физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.
где d l — вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r —радиус-вектор, проведанный из элемента d l проводника в точку А поля, r — модуль радиуса-вектора r. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление d B, если поступательное движение винта соответствует направлению тока в элементе. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами d l и r), выразив через него все остальные величины.
Магнитное поле в центре кругового проводника с током - все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов d B можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin a =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R.
3) Циркуляция вектора напряженности магнитного поля. Поле соленоида и тороида. Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]:
Здесь
Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле однородно, вне соленоида — неоднородно и практически отсутствует.
Важное практическое значение имеет также магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора. Магнитное поле сосредоточено внутри тороида, а вне его поле равно нулю.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 6297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.009 с.) |


 (1)
(1)
 (2)
(2)



 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд
магнитное поле действует на заряд  , движущийся со скоростью
, движущийся со скоростью  .
. , равна
, равна 

 где
где  — магнитная постоянная. (4П*10^-7 Гн/м)
— магнитная постоянная. (4П*10^-7 Гн/м)


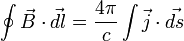
 — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:
— плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:
 Поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида).
Поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида).



