Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон био-савара-лапласа и его применение к расчету магнитного поля прямого и кругового токов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Закон Био — Савара — Лапласа для проводника с током I, элемент которого d l создает в некоторой точке А (рис. 164) индукцию поля d B, записывается в виде
где d l — вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r — радиус-вектор,
Модуль вектора d B определяется выражением
где а — угол между векторами dl и г. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера. 1. Магнитное поле прямого тока — тока, текущего по тонкому прямому про
(радиус дуги CD вследствие малости d l равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),
Следовательно, магнитная индукция поля прямого тока
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка. Поэтому сложение векторов d B можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
Тогда
Следовательно, магнитная индукция поля в центре кругового проводника с током
18. Поток магнитного поля. Теорема Гаусса для Ḃ. Потоком вектора магнитной индукции (магнитным потоком) через площадку Единица: вебер (Вб). Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору Теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
19. Теорема о циркуляции вектора Ḃ, её применение к расчету полей. Поле соленоида. Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био-Савара-Лапласа. 1). Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока 1, перпендикулярного плоскости чертежа и направленного к нам (рис. 13). Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности. Следовательно, циркуляция вектора В равна
Рис.13. Рис.14. Согласно выражению (9.2), получим В 2π r = μo I (в вакууме), откуда В = μo I /(2π r). Таким образом, исходя из теоремы о циркуляции вектора В, получили выражение для магнитной индукции поля прямого тока, выведенное выше (2.6). 2). Рассчитаем индукцию магнитного поля внутри соленоида – цилиндрической катушки, состоящей из большого числа витков равномерно намотанных на общий сердечник. Рассмотрим соленоид длиной l, имеющий n витков, по которому течет ток I (рис.14). Длину соленоида считаем во много раз большей, чем диаметр его витков, т.е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида, проведенное с помощью железных опилок показывает, что внутри соленоида поле является однородным, вне соленоида неоднородным и очень слабым, т.е. его можно практически считать равным нулю. Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, АВСDА, и охватывающему все n витков согласно (9.2), равна
Интеграл по АВСDА можно представить в виде двух – по внешнему участку ABCD (он равен нулю, так как вне соленоида В =0) и по внутреннему DA.
На участке DА циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,
Отсюда приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме): B = μ o nI / l. (10.2) Получили, что поле внутри соленоида однородно. 3). Важное значение для практики имеет также магнитное поле тороида – кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора. Магнитное поле сосредоточено внутри тороида, вне его поле отсутствует. Тороид можно рассматривать как достаточно длинный соленоид свитый в кольцо и для расчета напряженности магнитного поля тороида пользоваться формулой (10.2): В = μ o nI / l = μ o nI /(2 πr). (10.3) Причем длину тороида l следует считать по средней линии, пренебрегая небольшим различием между внешней и внутренней окружностями кольца.
Сила Ампера. Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы.
Формула 1 — Закон Ампера B индукция магнитного поля, в котором находится проводник с током I сила тока в проводнике dl бесконечно малый элемент длинны проводника с током альфа угол между индукцией внешнего магнитного поля и направлением тока в проводнике Направление силы Ампера находится по правилу левой руки. Формулировка этого правила, звучит так. Когда левая рука расположена таким образом, что лини магнитной индукции внешнего поля входят в ладонь, а четыре вытянутых пальца указывают направление движения тока в проводнике, при этом отогнутый под прямым углом большой палец будет указывать направление силы, которая действует на элемент проводника.
Рисунок 1 — правило левой руки
Некоторые проблемы возникают, при использовании правила левой руки, в случае если угол между индукцией поля и током маленький. Трудно определить, где должна находиться открытая ладонь. Поэтому для простоты применения этого правила, можно ладонь располагать так, чтобы в нее входил не сам вектор магнитной индукции, а его модуль.
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 11857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |


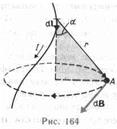 проведенный из элемента d l проводника в точку А поля, r — модуль радиуса-вектора г. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление d B, если поступательное движение винта соответствует направлению тока в элементе.
проведенный из элемента d l проводника в точку А поля, r — модуль радиуса-вектора г. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление d B, если поступательное движение винта соответствует направлению тока в элементе.

 воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами d l и r), выразив через него все остальные величины. Из рис. 165 следует, что
воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами d l и r), выразив через него все остальные величины. Из рис. 165 следует, что
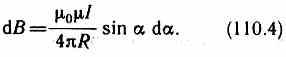





 наз. скалярная величина
наз. скалярная величина  , где
, где  угол между векторами
угол между векторами 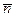 (вектор нормали к плоскости контура) и
(вектор нормали к плоскости контура) и  .
. .
.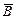 :
:  . Магнитный поток
. Магнитный поток  сквозь поверхность с площадью
сквозь поверхность с площадью  находится алгебраическим суммированием потоков
находится алгебраическим суммированием потоков  сквозь участки поверхности.
сквозь участки поверхности. .
.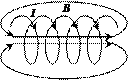 Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

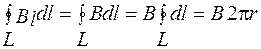
 . (10.1)
. (10.1)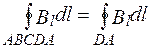 .
. .
.