
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения электрического заряда.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон сохранения электрического заряда. Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) –избыток отрицательного заряда. Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами. Если выбрать в качестве объекта исследования электрически изолированную систему, т. е. такую, через ограничивающую поверхность которой не могут проходить заряженные тела или частицы, то алгебраическая сумма зарядов в этой системе остается постоянной. Этот экспериментально установленный факт свидетельствует о существовании закона сохранения электрического заряда: в электрически изолированной системе суммарный заряд не изменяется
где заряд любого наэлектризованного тела, а также частиц, из которых это тело состоит, является кратным некоторому элементарному значению
где Выражение (1.2) описывает свойство электрических зарядов – дискретность. Носителем элементарного отрицательного заряда является электрон. Минимальную порцию положительного заряда имеют протон и позитрон. Электрический заряд любого тела является, таким образом, совокупностью элементарных зарядов, входящих в состав этого тела. Если тело заряжено отрицательно, это означает, что отрицательных элементарных частиц в этом теле больше, чем положительных, а у положительно заряженного тела –наоборот. Отсюда становится ясно, что незаряженное (нейтральное) тело – это тело, в котором количество отрицательных элементарных зарядов равно количеству положительных, а процесс электризации тела – это нарушение в пределах данного тела указанного равенства зарядов. Электрический заряд обладает также свойством инвариантности. Это означает, что величина заряда тела (частицы) не изменяется при переходе от одной инерциальной системы отсчета к другой, т. е. не зависит от скорости движения заряда. Инвариантность заряда подтверждается фактом нейтральности атомов и молекул. Если бы заряды зависели от скорости их движения (а скорость движения электронов в атомах и молекулах много больше скорости движения ядер, а значит, скорости протонов), то нарушалась бы нейтральность замкнутой системы (атома, молекулы). Однако нейтральность атомов и молекул доказана экспериментально с большой точностью.
Таким образом, релятивистская инвариантность заряда и закон сохранения заряда изолированной системы взаимно обусловлены и принимаются в качестве исходного положения электродинамики.
Электрическое поле. Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле[1], существующее вокруг тел или частиц, обладающихэлектрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела[2]. Пространство, в котором находятся электрические заряды, обладает основным свойством, а именно: на всякий другой заряд, внесенный в это пространство, действуют силы. Если в пространстве на внесенные тела действуют силы, то в этом пространстве существует силовое поле. Если электрическое поле создается неподвижными электрическими зарядами, то это – электростатическое поле. Существуют и другие виды силовых полей, воздействующих на пробные заряды. Так, поля,создаваемые равномерно движущимися зарядами, называются магнитными полями, а поля, создаваемые произвольно движущимися зарядами, – электромагнитными полями.
Для того чтобы охарактеризовать электрическое поле, можно провести его зондирование при помощи так называемого пробного заряда (пробный точечный положительный заряд – такой заряд, который не искажает исследуемое поле). Если в поле, создаваемое зарядом Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле
где E — напряжённость электрического поля, D — индукция электрического поля.
3. Напряженность электрического поля. Принцип суперпозиции для Ḕ. Напряженность электрического поля
формула остается справедливой и в том случае, когда в качестве пробного взят отрицательный заряд ( Из формул (1.4) и (1.5) следует, что напряженность поля точечного заряда пропорциональна величине заряда и обратно пропорциональна квадрату расстояния R от заряда до данной точки поля:
где Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Линии напряженности никогда не пересекаются. Линии Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности (рис. 1.3, в).
ПРИНЦИП СУПЕРП0ЗИЦИИ (наложения) полей: Напряженность Электростатическое поле очень наглядно можно изображать с помощью линий напряженности или силовых линий вектора 4. Поток вектора Ḕ. Теорема Гаусса и её применение к расчету поля вектора Ḕ.
Для однородного поля
Для неоднородного поля
где
В случае криволинейной поверхности S ее нужно разбить на элементарные поверхности dS, рассчитать поток
Поток вектора
Для однородного поля поток через замкнутую поверхность равен нуля. В случае неоднородного поля
ТЕОРЕМА ГАУССА: Поток вектора напряженности
II. Применение теоремы Гаусса. 1. Напряженность поля, создаваемая бесконечно протяженной однородно заряженной плоскоти с поверхностной плотностью заряда σ. ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ ЗАРЯДА показывает, какой заряд приходится на единицу площади
2. Напряженность поля, создаваемая двумя параллельными бесконечно протяженными пластинами с поверхностной плотностью зарядов +σ и -σ. Найден поле Е, используя принцип суперпозиции полей. В области между плоскостями
Слева и справа от плоскостей поля вычитаются, т.к. линии напряженности направлены навстречу друг другу
3. Напряженность ноля, создаваемая бесконечно протяжённой нитью с линейной плотностью заряда τ. Линейная плотность заряда показывает, какой заряд приходится на единицу длина проводника.
На сфере радиуса R распределен заряд q. Поверхностная плотность заряда
Линии напряженности направлены радиально, отходя от поверхности сфера под прямым углом. Окружаем данную сферу сферой радиуса r и определяем поток напряженности
При r > R весь заряд q попадает внутрь сфера r. Тогда по теореме Гаусса
При r < R внутри поверхности радиуса r зарядов нет и поэтому Е=0. На этом основано экранирование - защита от внешних электрических полей.
5. Напряженность поля объемно заряженного шара с объемной плотностью заряда ρ. Объемная плотность заряда показывает, какой заряд приходится на единицу объема
а) При r > R по пункту 4 находим
б) При r < R
Закон Джоуля-Ленца. Закон Джоуля-Ленца для участка цепи: Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка В математической форме этот закон имеет вид:
16. Магнитная индукция. Принцип суперпозиции для вектора Ḃ. Магнитная индукция
Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила
Свойства силовых линий магнитного поля: 1. Магнитные силовые линии замкнуты на себя и никогда не пересекаются; 2. Магнитные силовые линии стремятся сократиться до наименьшей длины, то есть обладают свойством продольного напряжения; 3. Одинаково направленные линии отталкиваются, противоположно направленные — притягиваются, то есть обладают свойством бокового распора; 4. Направление силового действия магнитных линий совпадает с направлением северного конца магнитной стрелки, помещенной в поле. Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:
Сила Ампера. Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы.
Формула 1 — Закон Ампера B индукция магнитного поля, в котором находится проводник с током I сила тока в проводнике dl бесконечно малый элемент длинны проводника с током альфа угол между индукцией внешнего магнитного поля и направлением тока в проводнике Направление силы Ампера находится по правилу левой руки. Формулировка этого правила, звучит так. Когда левая рука расположена таким образом, что лини магнитной индукции внешнего поля входят в ладонь, а четыре вытянутых пальца указывают направление движения тока в проводнике, при этом отогнутый под прямым углом большой палец будет указывать направление силы, которая действует на элемент проводника.
Рисунок 1 — правило левой руки
Некоторые проблемы возникают, при использовании правила левой руки, в случае если угол между индукцией поля и током маленький. Трудно определить, где должна находиться открытая ладонь. Поэтому для простоты применения этого правила, можно ладонь располагать так, чтобы в нее входил не сам вектор магнитной индукции, а его модуль.
Рисунок 2 — Параллельные проводники с током
Используя параллельные проводники и выражение силы Ампера для них можно определить единицу в один Ампер. Если по бесконечно длинным параллельным проводникам, находящимся на расстоянии в один метр, текут одинаковые токи силой в одни ампер, то силы взаимодействия между ними будет составлять в 2*10-7 Ньютона, на каждый метр длинны. Используя эту зависимость, можно выразить чему будет равен один Ампер. Уравнение Максвелла. Максвелл предположил, что изменяющееся электрическое поле создаёт магнитное поле. Но мы знаем, что постоянное магнитное поле создаётся токами. Поэтому естественно предположение, что должен быть ещё один ток, который Максвелл назвал током смещения и который ответственен за создание магнитного поля. Для установления вида этого тока смещения, рассмотрим соотношение (3.100) справа налево, а именно s =D. (3.101) Умножим обе части на площадь пластины S и получим q = sS= DS. (3.102) Здесь q – заряд пластины конденсатора. Во время заряда конденсатора ток в подводящем проводе
Разделив обе части последнего уравнения на площадь пластины S, получим слева ток проводимости j=I/S, а справа – плотность нового, максвелловского тока, или плотность тока смещения. Таким образом,
В последнем уравнении мы поставили значки векторов – для общего случая и написали частную производную, поскольку в общем случае вектор электрического смещения может зависеть и от координаты. Проанализировав полученные результаты, Максвелл ввёл понятие общего тока как суммы токов проводимости и тока смещения. Здесь подчеркнём, что ток смещения – это просто название изменяющегося во времени электрического поля. Единственная функция тока смещения – создавать магнитное поле. Тогда обобщенный закон полного тока будет иметь вид
или окончательно
Максвелл создал замкнутую макроскопическую теорию электромагнитного поля. В основе этой теории лежат его знаменитые уравнения. Первая пара связывает основные характеристики электрического и магнитного полей
В уравнении (3.107) под полем E надо понимать полное поле – поле, созданное неподвижными зарядами, и поле, созданное изменяющимся магнитным полем. Уравнение (3.108) отражает тот факт, что в природе нет магнитных зарядов. Вторая пара уравнений Максвелла связывает вспомогательные характеристики электрического и магнитного полей
Уравнение (3.109) является следствием того, что магнитное поле создаётся как токами проводимости, так и токами смещения (изменяющимся во времени электрическим полем). И уравнение (3.110) говорит нам, что источниками электрического поля (помимо изменяющегося магнитного поля) являются электрические заряды. Уравнения Максвелла (3.107)…(3.110) называются уравнениями Максвелла в интегральной форме. Уравнения Максвелла дополняются так называемыми материальными уравнениями, которые устанавливают связь между вспомогательными и основными характеристиками полей. Для однородной и изотропной неферромагнитной среды эти уравнения имеют вид
Уравнения Максвелла не симметричны относительно электрического и магнитного полей, поскольку в природе нет магнитных зарядов. Уравнения Максвелла позволили предсказать существование электромагнитных волн – распространяющихся в пространстве со скоростью света переменных электрического и магнитного полей. Вскоре электромагнитные волны были обнаружены немецким физиком Г.Герцем. Оказалось, что их свойства полностью описываются уравнениями Максвелла. Это также позволило Максвеллу создать электромагнитную теорию света – как электромагнитных волн с длиной волны Если применить к уравнениям (3.107)…(3.110) теоремы Гаусса и Стокса, то получим уравнения Максвелла в дифференциальной форме:
Уравнения (3.98)…(3.101) связывают локальные характеристики поля в каждой точке. Уравнение связи.
Опыты Герца и Лебедева. Экспериментальное подтверждение теории Максвелла удалось получить только Герцу в 1888 г. Источником электромагнитных волн, в принципе, может быть любой колебательный контур или проводник с переменным током, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое или магнитное поле. Но, как уже обсуждалось, интенсивность излучения зависит от параметров источника и пропорциональна четвертой степени частоте колебаний. Электромагнитные колебания легко возбуждаются в обычном колебательном контуре, но для увеличения интенсивности излучения необходимо, чтобы переменное поле создавалось в значительно большем объеме пространства.
Шарики разряжались, излучение прекращалось до тех пор, пока за счет источника между шариками опять не возникало напряжение равное напряжению пробоя. Для регистрации электромагнитных волн Герц использовал второй, точно такой же по геометрическим характеристикам вибратор. В этом случае собственные частоты первого вибратора и резонатора (рис.194 – Р) совпадали, а при их соответствующем взаимном расположении, в случае электромагнитной волны, в резонаторе возникала искра. Герцу удалось получить частоту колебаний порядка 100 МГц, что соответствовало длинам волн, которые можно зарегистрировать в лаборатории размерами до 15 м. Используя свинцовый экран для отражения волн, Герц по интенсивности искры в резонаторе фиксировал максимумы и минимумы возникших стоячих волн. Опыты Герца доказали: 1)распространение волн, 2)позволили получить волны с длиной волны от 0,4 м до 9,6 м и соответственно оценить скорость их распространения, 3)показали, что волны поперечные,4)отражаются от проводников, 5)преломляются в диэлектриках (для асфальтовой призмы массой порядка тонны при длине волны 0,6 м показатель преломления равнялся 1,69). Позднее П.Н.Лебедев, применяя миниатюрный вибратор из тонких платиновых стерженьков, получил миллиметровые электромагнитные волны с длиной волны 4-6 мм. П.Н.Лебедев в 1900 г. доказал существование светового давления на твердые тела, которое при средней мощности солнечного излучения, приходящего на Землю, составляет примерно 5 мкПа. Для этого Лебедеву пришлось решить проблему получения глубокого вакуума, в котором на крутильных весах была подвешена легкая рамка из двух дисков с размерами в доли миллиметров. Один из дисков был белый, чтобы обеспечить наиболее полное отражение, а второй – черный для полного поглощения. В ходе опыта давление на белый диск было примерно в 1,5 раза больше, чем на черный диск и, из-за разницы силы давлений на диски, рамка поворачивалась. В 1910 г. Лебедев доказал давление света и на газы. Опыты Лебедева имели огромное значения для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны. Закон сохранения электрического заряда. Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) –избыток отрицательного заряда. Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами. Если выбрать в качестве объекта исследования электрически изолированную систему, т. е. такую, через ограничивающую поверхность которой не могут проходить заряженные тела или частицы, то алгебраическая сумма зарядов в этой системе остается постоянной. Этот экспериментально установленный факт свидетельствует о существовании закона сохранения электрического заряда: в электрически изолированной системе суммарный заряд не изменяется
где заряд любого наэлектризованного тела, а также частиц, из которых это тело состоит, является кратным некоторому элементарному значению
где Выражение (1.2) описывает свойство электрических зарядов – дискретность. Носителем элементарного отрицательного заряда является электрон. Минимальную порцию положительного заряда имеют протон и позитрон. Электрический заряд любого тела является, таким образом, совокупностью элементарных зарядов, входящих в состав этого тела. Если тело заряжено отрицательно, это означает, что отрицательных элементарных частиц в этом теле больше, чем положительных, а у положительно заряженного тела –наоборот. Отсюда становится ясно, что незаряженное (нейтральное) тело – это тело, в котором количество отрицательных элементарных зарядов равно количеству положительных, а процесс электризации тела – это нарушение в пределах данного тела указанного равенства зарядов. Электрический заряд обладает также свойством инвариантности. Это означает, что величина заряда тела (частицы) не изменяется при переходе от одной инерциальной системы отсчета к другой, т. е. не зависит от скорости движения заряда. Инвариантность заряда подтверждается фактом нейтральности атомов и молекул. Если бы заряды зависели от скорости их движения (а скорость движения электронов в атомах и молекулах много больше скорости движения ядер, а значит, скорости протонов), то нарушалась бы нейтральность замкнутой системы (атома, молекулы). Однако нейтральность атомов и молекул доказана экспериментально с большой точностью.
Таким образом, релятивистская инвариантность заряда и закон сохранения заряда изолированной системы взаимно обусловлены и принимаются в качестве исходного положения электродинамики.
Электрическое поле. Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле[1], существующее вокруг тел или частиц, обладающихэлектрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела[2]. Пространство, в котором находятся электрические заряды, обладает основным свойством, а именно: на всякий другой заряд, внесенный в это пространство, действуют силы. Если в пространстве на внесенные тела действуют силы, то в этом пространстве существует силовое поле. Если электрическое поле создается неподвижными электрическими зарядами, то это – электростатическое поле. Существуют и другие виды силовых полей, воздействующих на пробные заряды. Так, поля,создаваемые равномерно движущимися зарядами, называются магнитными полями, а поля, создаваемые произвольно движущимися зарядами, – электромагнитными полями.
Для того чтобы охарактеризовать электрическое поле, можно провести его зондирование при помощи так называемого пробного заряда (пробный точечный положительный заряд – такой заряд, который не искажает исследуемое поле). Если в поле, создаваемое зарядом Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле
где E — напряжённость электрического поля, D — индукция электрического поля.
3. Напряженность электрического поля. Принцип суперпозиции для Ḕ. Напряженность электрического поля
формула остается справедливой и в том случае, когда в качестве пробного взят отрицательный заряд ( Из формул (1.4) и (1.5) следует, что напряженность поля точечного заряда пропорциональна величине заряда и обратно пропорциональна квадрату расстояния R от заряда до данной точки поля:
где Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Линии напряженности никогда не пересекаются. Линии Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности (рис. 1.3, в).
ПРИНЦИП СУПЕРП0ЗИЦИИ (наложения) полей: Напряженность Электростатическое поле очень наглядно можно изображать с помощью линий напряженности или силовых линий вектора 4. Поток вектора Ḕ. Теорема Гаусса и её применение к расчету поля вектора Ḕ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.012 с.) |

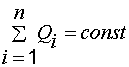
 – заряды входящих в систему объектов.
– заряды входящих в систему объектов. ,
, – целое число; е – элементарный заряд, равный
– целое число; е – элементарный заряд, равный  Кл.
Кл. , поместить пробный заряд
, поместить пробный заряд  , то на него действует сила
, то на него действует сила 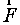 , согласно закону Кулона пропорциональная пробному заряду
, согласно закону Кулона пропорциональная пробному заряду  не зависит от
не зависит от 
 – это векторная величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы
– это векторная величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы .
. ). В этом случае векторы
). В этом случае векторы  ,
, – радиус-вектор, соединяющий местоположение точечного заряда, создающего электрическое поле, и исследуемую точку пространства.
– радиус-вектор, соединяющий местоположение точечного заряда, создающего электрическое поле, и исследуемую точку пространства.
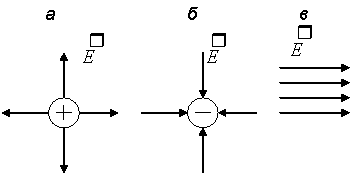 Рис. 1.3. Электростатическое поле точечного заряда; а – положительного; б – отрицательного; в – однородное электростатическое поле
Рис. 1.3. Электростатическое поле точечного заряда; а – положительного; б – отрицательного; в – однородное электростатическое поле
 результирующего поля, создаваемого системой зарядов, равна геометрической (векторной) сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
результирующего поля, создаваемого системой зарядов, равна геометрической (векторной) сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности. Определим поток вектора
Определим поток вектора  через произвольную поверхность dS,
через произвольную поверхность dS,  - нормаль к поверхности.α - угол между нормалью и силовой линией вектора
- нормаль к поверхности.α - угол между нормалью и силовой линией вектора  . ПОТОКОМ ВЕКТОРА
. ПОТОКОМ ВЕКТОРА 
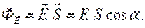

 - проекция
- проекция  - проекция
- проекция 
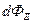 через элементарную поверхность, а общий поток будет равен сумме или в пределе интегралу от элементарных потоков
через элементарную поверхность, а общий поток будет равен сумме или в пределе интегралу от элементарных потоков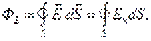 где
где 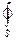 - интеграл по замкнутой поверхности S (например, по сфере, цилиндру, кубу и т.д.)
- интеграл по замкнутой поверхности S (например, по сфере, цилиндру, кубу и т.д.) является алгебраической величиной: зависит не только от конфигурации поля
является алгебраической величиной: зависит не только от конфигурации поля 
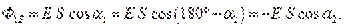


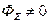 .
.
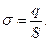



 .
.
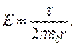


 , т.к. Е n = E.
, т.к. Е n = E.




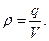




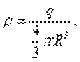





 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд
магнитное поле действует на заряд  , движущийся со скоростью
, движущийся со скоростью  .
. , с которой магнитное поле действует на элемент объёма dV проводника с током плотности
, с которой магнитное поле действует на элемент объёма dV проводника с током плотности 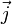 , находящегося в магнитном поле с индукцией
, находящегося в магнитном поле с индукцией 

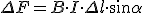


 . (3.103)
. (3.103) . (3.104)
. (3.104) , (3.105)
, (3.105) . (3.106)
. (3.106) ; (3.107)
; (3.107) . (3.108)
. (3.108) ; (3.109)
; (3.109)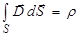 . (3.110)
. (3.110) (3.111)
(3.111) .
. ; (3.112)
; (3.112) ; (3.113)
; (3.113) ; (3.114)
; (3.114) . (3.115)
. (3.115) Вектора
Вектора  описывают соответствия электрического и магнитного поля
описывают соответствия электрического и магнитного поля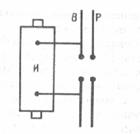 Поскольку
Поскольку  ,
,  ,
,  , то Герц, в своих опытах, уменьшая число витков катушки и увеличивая расстояние между обкладками конденсатора, преобразовал «закрытый» колебательный контур в «открытый» (рис.194), который представлял собой, практически два металлических шарика, соединенных проводником.
, то Герц, в своих опытах, уменьшая число витков катушки и увеличивая расстояние между обкладками конденсатора, преобразовал «закрытый» колебательный контур в «открытый» (рис.194), который представлял собой, практически два металлических шарика, соединенных проводником. Как уже обсуждалось, эта система называется, в его честь, вибратором Герца. Шарики – вибратор (В) Герца, заряжались за счет источника (рис.195), который является индуктором (И) электромагнитных колебаний. Когда напряжение между шариками достигало пробивного значения, возникала искра, т.е. переменный ток, а следовательно переменное электромагнитное поле.
Как уже обсуждалось, эта система называется, в его честь, вибратором Герца. Шарики – вибратор (В) Герца, заряжались за счет источника (рис.195), который является индуктором (И) электромагнитных колебаний. Когда напряжение между шариками достигало пробивного значения, возникала искра, т.е. переменный ток, а следовательно переменное электромагнитное поле.


