
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вихревое электрическое поле. Ток смещения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Причина возникновения электрического тока в неподвижном проводнике - электрическое поле.
Чем быстрее меняется магнитная индукция, тем болыпе напряженность электрического поля. Согласно правилу Ленца при возрастании магнитной индукции Направление силовых линий напряженности Дав формулировку закона Фарадея, зависящую не от конкретных проводников и их движений, а от характеристик полей Уравнение Максвелла. Максвелл предположил, что изменяющееся электрическое поле создаёт магнитное поле. Но мы знаем, что постоянное магнитное поле создаётся токами. Поэтому естественно предположение, что должен быть ещё один ток, который Максвелл назвал током смещения и который ответственен за создание магнитного поля. Для установления вида этого тока смещения, рассмотрим соотношение (3.100) справа налево, а именно s =D. (3.101) Умножим обе части на площадь пластины S и получим q = sS= DS. (3.102) Здесь q – заряд пластины конденсатора. Во время заряда конденсатора ток в подводящем проводе
Разделив обе части последнего уравнения на площадь пластины S, получим слева ток проводимости j=I/S, а справа – плотность нового, максвелловского тока, или плотность тока смещения. Таким образом,
В последнем уравнении мы поставили значки векторов – для общего случая и написали частную производную, поскольку в общем случае вектор электрического смещения может зависеть и от координаты. Проанализировав полученные результаты, Максвелл ввёл понятие общего тока как суммы токов проводимости и тока смещения. Здесь подчеркнём, что ток смещения – это просто название изменяющегося во времени электрического поля. Единственная функция тока смещения – создавать магнитное поле. Тогда обобщенный закон полного тока будет иметь вид
или окончательно
Максвелл создал замкнутую макроскопическую теорию электромагнитного поля. В основе этой теории лежат его знаменитые уравнения. Первая пара связывает основные характеристики электрического и магнитного полей
В уравнении (3.107) под полем E надо понимать полное поле – поле, созданное неподвижными зарядами, и поле, созданное изменяющимся магнитным полем. Уравнение (3.108) отражает тот факт, что в природе нет магнитных зарядов. Вторая пара уравнений Максвелла связывает вспомогательные характеристики электрического и магнитного полей
Уравнение (3.109) является следствием того, что магнитное поле создаётся как токами проводимости, так и токами смещения (изменяющимся во времени электрическим полем). И уравнение (3.110) говорит нам, что источниками электрического поля (помимо изменяющегося магнитного поля) являются электрические заряды. Уравнения Максвелла (3.107)…(3.110) называются уравнениями Максвелла в интегральной форме. Уравнения Максвелла дополняются так называемыми материальными уравнениями, которые устанавливают связь между вспомогательными и основными характеристиками полей. Для однородной и изотропной неферромагнитной среды эти уравнения имеют вид
Уравнения Максвелла не симметричны относительно электрического и магнитного полей, поскольку в природе нет магнитных зарядов. Уравнения Максвелла позволили предсказать существование электромагнитных волн – распространяющихся в пространстве со скоростью света переменных электрического и магнитного полей. Вскоре электромагнитные волны были обнаружены немецким физиком Г.Герцем. Оказалось, что их свойства полностью описываются уравнениями Максвелла. Это также позволило Максвеллу создать электромагнитную теорию света – как электромагнитных волн с длиной волны Если применить к уравнениям (3.107)…(3.110) теоремы Гаусса и Стокса, то получим уравнения Максвелла в дифференциальной форме:
Уравнения (3.98)…(3.101) связывают локальные характеристики поля в каждой точке. Уравнение связи.
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 Индукционное электрическое поле является вихревым.
Индукционное электрическое поле является вихревым. 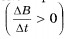 направление вектора напряженности
направление вектора напряженности 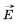 электрического поля образует левый винт с направлением вектора
электрического поля образует левый винт с направлением вектора  . Это означает, что при вращении винта с левой нарезкой в направлении линий напряженности электрического поля поступательное перемещение винта совпадает с направлением вектора магнитной индукции. Напротив, при убывании магнитной индукции
. Это означает, что при вращении винта с левой нарезкой в направлении линий напряженности электрического поля поступательное перемещение винта совпадает с направлением вектора магнитной индукции. Напротив, при убывании магнитной индукции  = q
= q  и
и  , Максвелл задумался над источниками магнитных полей. Получалось, что электрические поля порождаются как зарядами, так и переменным магнитным полем, магнитные же поля – только движущимися зарядами. Максвелл, пытаясь обобщить закон Ампера, показал, что если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
, Максвелл задумался над источниками магнитных полей. Получалось, что электрические поля порождаются как зарядами, так и переменным магнитным полем, магнитные же поля – только движущимися зарядами. Максвелл, пытаясь обобщить закон Ампера, показал, что если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения. . (3.103)
. (3.103) . (3.104)
. (3.104) , (3.105)
, (3.105) . (3.106)
. (3.106) ; (3.107)
; (3.107) . (3.108)
. (3.108) ; (3.109)
; (3.109)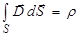 . (3.110)
. (3.110) (3.111)
(3.111) .
. ; (3.112)
; (3.112) ; (3.113)
; (3.113) ; (3.114)
; (3.114) . (3.115)
. (3.115) Вектора
Вектора  описывают соответствия электрического и магнитного поля
описывают соответствия электрического и магнитного поля


