
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные затухающие электромагнитные колебания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Свободные затухающие колебания – это такие колебания, амплитуда которых уменьшается с течением времени вследствие потерь энергии колебательной системой. В электрическом колебательном контуре энергия расходуется на джоулево тепло и на электромагнитное излучение. Мы рассматривали процесс колебаний в контуре без потерь. Однако в реальных контурах всегда происходят необратимые потери энергии на нагрев проводов и диэлектрика, а также на излучение, что приводит к постепенному уменьшению амплитуды электрических колебаний, или, как говорят, к их затуханию. При расчете затухания контура полагают, что он имеет сосредоточенное сопротивление, потребляющее то же количество энергии, которое расходуется в контуре на все виды потерь.
Поскольку мощность потерь пропорциональна активному сопротивлению контура, а развиваемая в его элементах реактивная мощность пропорциональна их реактивным сопротивлениям, то добротность характеризует также отношение этих мощностей. Чем больше добротность, тем медленнее затухают свободные колебания в контурах с одинаковой частотой собственных колебаний. Используемые в радиотехнике контуры из катушек и конденсаторов обычно имеют добротность от 50 до 300. Энергия, получаемая антенной передатчика из колебательного контура, распространяется в пространстве в виде электромагнитных волн. Расстояние. которое проходит такая волна за время, равное периоду колебаний, называется длиной волны λ. В соответствии с этим определением λ= υТ= υ/fо,где υ- скорость распространения электромагнитных волн. Для любой среды υ = с/ ε μ, где с- скорость распространения света в вакууме, 3.108 м/сек,ε μ-соответственно относительные диэлектрическая и магнитная постоянные среды. Для воздуха можно считать υ=с и,следовательно, если подставить υ в м/сек,а fо в Мгц, то λ(м)=300/fо(Мгц). Дифференциальное уравнение затухающих электрических колебаний в контуре, имеющем электрическое сопротивление
где Уравнение затухающих колебаний в случае слабого затухания (
где Время релаксации – это промежуток времени
Время релаксации связано с коэффициентом затухания соотношением
Логарифмический декремент затухания колебаний
где Формула, связывающая логарифмический декремент колебаний с коэффициентом затухания и периодом затухающих колебаний:
30. Вынужденные электромагнитные колебания. Вынужденные колебания – это такие колебания, которые совершаются при наличии внешнего периодически изменяющегося воздействия. Дифференциальное уравнение вынужденных электрических колебаний в контуре, имеющем электрическое сопротивление
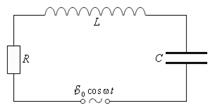
Рис. 4.3. Контур для наблюдения вынужденных электрических колебаний Уравнение установившихся вынужденных электрических колебаний:
где Амплитуда установившихся вынужденных колебаний заряда конденсатора
Разность фаз колебаний заряда конденсатора и вынуждающей ЭДС источника тока
Амплитуда вынужденных колебаний зависит от соотношения между циклическими частотами вынуждающего воздействия
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.009 с.) |

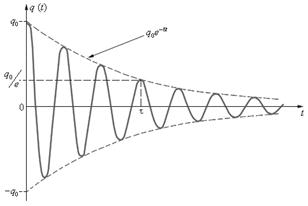 Колебания в контуре затухают тем быстрее, чем большая доля первоначально запасенной в контуре энергии теряется за период колебаний, т. е. чем больше сопротивление потерь по сравнению с его характеристическим сопротивлением. Отношение характеристического сопротивления контура, к сопротивлению потерь называется добротностью:
Колебания в контуре затухают тем быстрее, чем большая доля первоначально запасенной в контуре энергии теряется за период колебаний, т. е. чем больше сопротивление потерь по сравнению с его характеристическим сопротивлением. Отношение характеристического сопротивления контура, к сопротивлению потерь называется добротностью: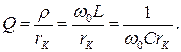
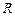 :
: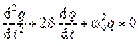 ,
,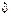 – коэффициент затухания,
– коэффициент затухания, 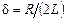 (здесь
(здесь 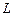 – индуктивность контура).
– индуктивность контура).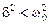 ) (рис. 4.2):
) (рис. 4.2):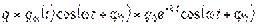 ,
, – амплитуда затухающих колебаний заряда конденсатора;
– амплитуда затухающих колебаний заряда конденсатора; 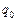 – начальная амплитуда колебаний;
– начальная амплитуда колебаний; 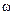 – циклическая частота затухающих колебаний,
– циклическая частота затухающих колебаний, 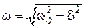 .
.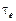 , в течение которого амплитуда колебаний уменьшается в
, в течение которого амплитуда колебаний уменьшается в 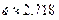 раз:
раз: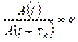 .
.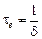 .
.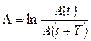 ,
,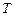 – период затухающих колебаний.
– период затухающих колебаний.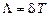 .
.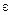 , изменяющейся по гармоническому закону
, изменяющейся по гармоническому закону 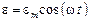 , где
, где 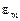 – амплитудное значение ЭДС, а
– амплитудное значение ЭДС, а 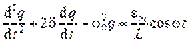 ,
, где
где 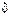 – коэффициент затухания,
– коэффициент затухания, 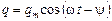 ,
,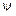 – разность фаз колебаний заряда конденсатора и вынуждающей ЭДС источника тока.
– разность фаз колебаний заряда конденсатора и вынуждающей ЭДС источника тока.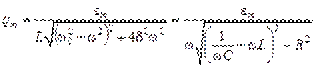 .
.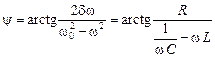 .
.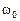 . Резонансная частота и резонансная амплитуда:
. Резонансная частота и резонансная амплитуда: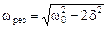 ;
; 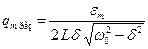 .
.


