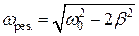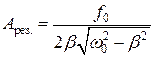Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие механические колебанияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
8 . Характеристики затухающих колебаний 1. Коэффициент затухания 2. Время затухания t - время, за которое «амплитуда» колебаний уменьшается в e раз.
Þ 3. Декремент затухания l – число, равное отношению «амплитуд», соответствующих моментам времени, отличающимся на период.
4. Логарифмический декремент затухания d.
Т.к. коэффициент затухания
За время затухания t система успевает совершить
5. Добротность – безразмерная физическая величина Q, пропорциональная отношению энергии W (t) колебаний системы в некоторый момент времени t к убыли этой энергии за период колебаний, т.е. за интервал времени (t, t + T). Коэффициент пропорциональности равен 2p.
Т.к. энергия колебаний W (t) пропорциональна квадрату амплитуды колебаний:
При малых значениях логарифмического декремента затухания (
При этом период T затухающих колебаний практически равен периоду T 0 свободных незатухающих колебаний, так что
Чем медленнее происходит затухание свободных колебаний, тем выше добротность Q колебательной системы. Добротность системы, совершающей незатухающие гармонические колебания, равна бесконечности. 9. Вынужденные колебания. Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (будем называть ее вынуждающей силой). Дифференциальное уравнение вынужденных колебаний имеет вид:
Введем обозначения:
В результате имеем следующее уравнение вынужденных колебаний:
Рассмотрим установившееся движение системы, которое возникает после того, как собственные колебания, возбужденные внешней силой уже затухнут. В установившемся режиме частота колебаний равна частоте вынуждающей силы. Поэтому будем искать решение уравнения (1.9.4) в установившемся режиме в виде:
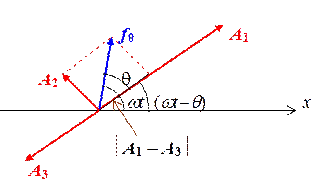
Воспользуемся методом векторных диаграмм. Для этого сопоставим каждому члену уравнения (1.9.4) вектор, вращающийся с угловой скоростью w, модуль которого равен амплитудному значению этого члена.
На рисунке 1.9.3 приведены соответствующие векторы, при этом
Рис. 1.9.3. С помощью теоремы Пифагора получим
Из теории дифференциальных уравнений известно, что общее решение x (t) неоднородного дифференциального уравнения (1.9.4) представляется в виде суммы частного решения неоднородного уравнения (1.9.5), которое мы нашли, и решения однородного дифференциального уравнения (когда в правой части уравнения (1.9.4) стоит 0, таким уравнением является уравнение (1.8.3)). В результате получим, что решением уравнения (1.9.4) является функция
где Если начальные условия колебательной системы следующие:
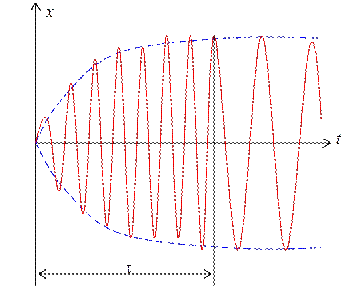
то график функции (1.9.9) имеет вид, показанный на рис. 1.9.4.
Рис. 1.9.4. Как видно из рисунка 1.9.4 в течение времени t < t происходит затухание свободных колебаний (установление колебаний). Такой режим колебаний называется переходным режимом. При Резонанс Резкое возрастание амплитуды вынужденных колебаний при приближении циклической частоты возмущающей силы к собственной частоте колебаний называется резонансом. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.
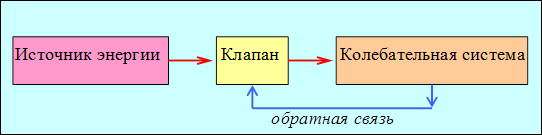
Автоколебания. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах – автоколебаниями. На рис. 1.10.1 изображена схема автоколебательной системы. В автоколебательной системе можно выделить три характерных элемента – колебательная система, источник энергии и клапан – устройство, осуществляющее обратную связь между колебательной системой и источником энергии.
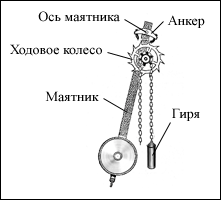
Рис. 1.10.1. Обратная связь называется положительной, если источник энергии производит положительную работу, т.е. передает энергию колебательной системе. В этом случае в течение промежутка времени, пока на колебательную систему действует внешняя сила, направление силы и направление скорости колебательной системы совпадают, в результате в системе происходят незатухающие колебания. Если направления силы и скорости противоположны, то имеет место отрицательная обратная связь, которая только усиливает затухание колебаний. Примером механической автоколебательной системы может служить часовой механизм (рис. 1.10.2). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменяется пружиной, а маятник – балансиром – маховичком, скрепленным со спиральной пружиной. Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь – клапаном, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод. Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику. Механические автоколебательные системы широко распространены в окружающей нас жизни и в технике. Автоколебания совершают паровые машины, двигатели внутреннего сгорания, электрические звонки, струны смычковых музыкальных инструментов, воздушные столбы в трубах духовых инструментов, голосовые связки при разговоре или пении и т. д.
Рис. 1.10.2.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1041; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.009 с.) |

 Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.
Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

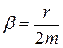 .
.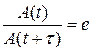 , (1.8.12)
, (1.8.12)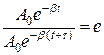 , Þ
, Þ 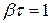 , Þ
, Þ 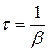 .
.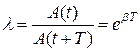 . (1.8.14)
. (1.8.14)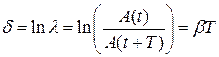 . (1.8.15)
. (1.8.15)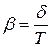 , то «амплитуда» A (t) может быть представлена в виде:
, то «амплитуда» A (t) может быть представлена в виде: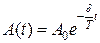 . (1.8.16)
. (1.8.16)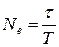 колебаний. Тогда, т.к.
колебаний. Тогда, т.к. 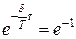 , то
, то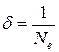 . (1.8.17)
. (1.8.17)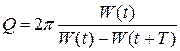 . (1.8.18)
. (1.8.18)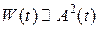 , то
, то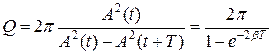 , Þ
, Þ 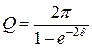 . (1.8.19)
. (1.8.19)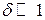 )
) 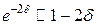 , тогда добротность системы равна
, тогда добротность системы равна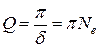 . (1.8.20)
. (1.8.20)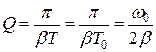 . (1.8.21)
. (1.8.21)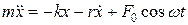 . (1.9.2)
. (1.9.2)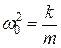 ,
, 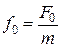 . (1.9.3)
. (1.9.3)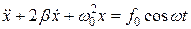 . (1.9.4)
. (1.9.4)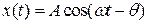 . (1.9.5)
. (1.9.5)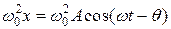 ® A 1,
® A 1,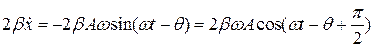 ® A 2, (1.9.6)
® A 2, (1.9.6)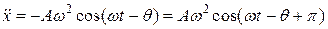 ® A 3,
® A 3,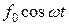 ® f 0.
® f 0.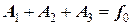 .
.
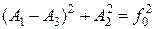 , Þ
, Þ 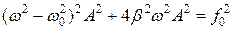 , Þ
, Þ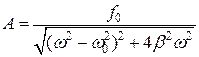 , (1.9.7)
, (1.9.7)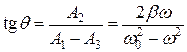 . (1.9.8)
. (1.9.8)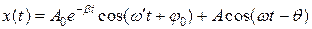 , (1.9.9)
, (1.9.9)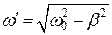 , A 0 и j 0 – произвольные постоянные, зависящие от начальных условий, A и q определяются уравнениями (1.9.7) и (1.9.8).
, A 0 и j 0 – произвольные постоянные, зависящие от начальных условий, A и q определяются уравнениями (1.9.7) и (1.9.8).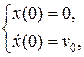
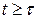 - установившийся режим. Время t, в течение которого происходит установление колебаний называется временем релаксации (оно равно времени затухания свободных затухающих колебаний:
- установившийся режим. Время t, в течение которого происходит установление колебаний называется временем релаксации (оно равно времени затухания свободных затухающих колебаний: