
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания в среде без сопротивления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим колебания материальной точки, происходящие под действием одной восстанавливающей силы
Характеристическое уравнение этого дифференциального уравнения
где С 1 и С 2 – постоянные интегрирования, определяемые из начальных условий:
Продифференцируем функцию
Получим
Подставив С 1 и С 2 в уравнение, запишем закон движения точки
и преобразуем его к более удобному виду. Введя обозначения
Получим
или
Таким образом, свободные колебания материальной точки в среде без сопротивления являются гармоническими. Амплитуда этих колебаний равна А, фаза
Свободные колебания в среде с сопротивлением Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы и силы сопротивления. Дифференциальное уравнение такого движения получим, воспользовавшись
Его характеристическое уравнение
Характер движения точки существенно зависит от соотношения величин n и k. Рассмотрим три возможных случая этого соотношения. Случай малого сопротивления Корни характеристического уравнения комплексно сопряженные:
где постоянные интегрирования С 1 и С 2 определяют из начальных условий. Введем новые постоянные А и φ0 с помощью соотношений
тогда из уравнения получим
Это уравнение описывает затухающие колебания, график которых приведен на рис. 2.6. Они не являются периодическими, но промежуток времени между двумя последовательными максимальными отклонениями точки от положения равновесия в одну и ту же сторону остается неизменным. Эту величину условно называют периодом затухающих колебаний: Скорость затухания колебаний характеризуется отношением величин двух последовательных максимальных отклонений точки от положения равновесия в одну и ту же сторону
которое называют декрементом колебаний. Используют также натуральный логарифм этой величины
Случай критического сопротивления Корни характеристического уравнения вещественные, равные и отрицательные
Случай большого сопротивления Корни характеристического уравнения вещественные, отрицательные и различные, а общее решение дифференциального уравнения имеет вид:
В двух последних случаях движение точки теряет колебательный характер и становится апериодическим. В зависимости от величины и направления начальной скорости график колебаний имеет вид одной из трех кривых, приведенных на рис. 2.7.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 . Такие колебания называют свободными и описывают однородным дифференциальным уравнением, которое можно получить из дифференциального уравнения прямолинейных колебаний материальной точки (
. Такие колебания называют свободными и описывают однородным дифференциальным уравнением, которое можно получить из дифференциального уравнения прямолинейных колебаний материальной точки (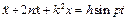 ), положив n = 0 и h = 0,
), положив n = 0 и h = 0,
 имеет чисто мнимые корни
имеет чисто мнимые корни  , поэтому общее решение уравнения запишем в виде:
, поэтому общее решение уравнения запишем в виде: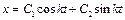


 .
.

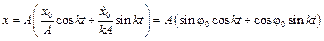

 , где
, где  – начальная фаза. Величину
– начальная фаза. Величину  называют круговой или циклической частотой колебаний. Период колебаний
называют круговой или циклической частотой колебаний. Период колебаний  является периодом функции
является периодом функции  . Последнее соотношение показывает, что круговая частота k равна числу полных колебаний точки за 2π секунд: k = 2π/ T. Таким образом, частота и период гармонических колебаний зависят от массы точки и коэффициента пропорциональности восстанавливающей силы, но не зависят от начальных условий. Это свойство свободных колебаний называют изохронностью. Амплитуда и начальная фаза зависят как от параметров системы m и c, так и от начальных условий.
. Последнее соотношение показывает, что круговая частота k равна числу полных колебаний точки за 2π секунд: k = 2π/ T. Таким образом, частота и период гармонических колебаний зависят от массы точки и коэффициента пропорциональности восстанавливающей силы, но не зависят от начальных условий. Это свойство свободных колебаний называют изохронностью. Амплитуда и начальная фаза зависят как от параметров системы m и c, так и от начальных условий.
 .
. имеет корни
имеет корни .
.
 , где
, где  . Общее решение дифференциального уравнения имеет вид:
. Общее решение дифференциального уравнения имеет вид: ,
, ,
,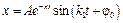 . (2.14)
. (2.14) , где k 1 – частота затухающих колебаний.
, где k 1 – частота затухающих колебаний.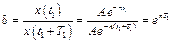 ,
,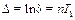 , называемый логарифмическим декрементом колебаний. Поскольку частота затухающих колебаний
, называемый логарифмическим декрементом колебаний. Поскольку частота затухающих колебаний  меньше частоты незатухающих колебаний k, появление силы сопротивления приводит к увеличению периода колебаний:
меньше частоты незатухающих колебаний k, появление силы сопротивления приводит к увеличению периода колебаний:  . Это изменение может быть весьма незначительным и поэтому основным влиянием, которое оказывает сила сопротивления на свободные колебания, является качественное изменение характера колебаний, которые становятся затухающими.
. Это изменение может быть весьма незначительным и поэтому основным влиянием, которое оказывает сила сопротивления на свободные колебания, является качественное изменение характера колебаний, которые становятся затухающими.

 , а общее решение дифференциального уравнения имеет вид:
, а общее решение дифференциального уравнения имеет вид: .
.
 .
.



