
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания линейной системы с одной степенью свободы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вынужденные колебания возникают в механической системе в результате воздействия на нее внешних (обычно периодических) возмущающих сил или ударов (импульсов). Мы начнем с разбора простейшего случая, когда внешняя возмущающая сила изменяется по гармоническому закону
где Н — максимальное значение или амплитуда возмущающей силы; p — число полных циклов изменения силы за 2π секунд. Уравнение колебаний линейного осциллятора в предположении, что, кроме силы Q, на него действует восстанавливающая сила, пропорциональная отклонению q, и сопротивление отсутствует, напишем следующим образом:
или
где Общее решение этого уравнения при p≠k получится как сумма общего решения однородного уравнения
и частного решения уравнения (1.10):
здесь C1 и C2 — произвольные постоянные. Пусть при
и
Первые два слагаемых правой части уравнения (2.28) соответствуют свободным колебаниям с собственной частотой k, т. е. колебаниям, какие совершал бы осциллятор в отсутствие возмущающей силы. При так называемых нулевых начальных условиях, когда Третье слагаемое — гармоническое колебание, происходящее с собственной частотой k, но с амплитудой, зависящей от возмущающей силы. Это колебание также относится к свободным колебаниям. Оно всегда сопровождает вынужденные колебания, при любых начальных условиях, от которых оно вообще не зависит. Его мы будем называть свободным сопровождающим колебанием. Четвертое слагаемое
представляет чисто вынужденные колебания осциллятора. Таким образом, колебания линейного осциллятора в рассматриваемом случае представляют линейное наложение трех гармонических колебаний: 1) свободных; 2) сопровождающих свободных и 3) чисто вынужденных. Отметим следующие свойства вынужденных колебаний, вытекающие из уравнения (1.12). а) Вынужденные колебания происходят с частотой возмущающей силы. б) Вынужденные колебания в отличие от свободных ни в чем не зависят от начальных условий. Поэтому для изменения, например, амплитуды вынужденных колебаний необходимы (при заданной возмущающей силе) существенные изменения параметров системы: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменения начального отклонения или начальной скорости. в) Если k>p, то знак отклонения будет совпадать со знаком силы Q, т. е. сила и вызванные ею вынужденные перемещения будут находиться в одной фазе. Если k<p, то знак силы будет противоположен знаку отклонения. Переписав для этого случая уравнение (2.29) следующим образом:
мы можем сказать, что при k < p возмущающая сила и вызванные ею колебания находятся в противоположных фазах. г) Когда k=p, выражение (1.12) теряет смысл. Теряет смысл также и слагаемое общего решения (1.11), соответствующее свободным сопровождающим колебаниям. Однако рассматриваемые совместно, оба названные слагаемые при k=p дают только неопределенность
которую можно раскрыть по правилу Лопиталя, заменив дробь в квадратных скобках пределом при p→k отношения производных по р от числителя и знаменателя:
Таким образом, общий интеграл (2.28) будет иметь вид
И здесь, как в (1.11), движение осциллятора представляет линейное наложение трех колебательных движений, но с одним существенным отличием от (1.11): вынужденные колебания представлены в нем непериодическим членом Рисунок 1.9. Изменение векового члена от времени.
При наличии сопротивления, которое мы, как и раньше, примем пропорциональным первой степени скорости q, положив
мы найдем только одно решение, годное для любых значений p, в частности, и для резонансного p=k. В самом деле, уравнение колебаний линейного осциллятора в прежних обозначениях будет в этом случае иметь вид
Его общее решение найдется как сумма общего решения уравнения без правой части:
и частного решения уравнения (1.13) с правой частью. Решения уравнения (1.14) при различных соотношениях между n и к нам известны. В частности, при n < k решение этого уравнения
определяет свободные затухающие колебания. Частное решение q 2 уравнения (1.13) мы будем искать, положив q2 = A sin (pt — ε) и подбирая величины А и е так, чтобы это выражение, будучи подставлено в уравнение (1.11), обратило его в тождество. Из уравнений
получающихся при сравнении коэффициентов при sin pt и cos pt в обеих частях уравнения (1.11), находим
Общий интеграл уравнения (1.11), таким образом, имеет вид
Если в начальный момент
Первые два слагаемых полученного решения соответствуют свободным и свободным сопровождающим колебаниям. И те, и другие с течением времени затухают, так что через более или менее продолжительный промежуток времени ими можно будет вообще пренебречь и считать, что в дальнейшем движении система совершает только чисто вынужденные колебания согласно уравнению
Этим уравнением будет определяться установившийся колебательный режим линейного осциллятора и при других соотношениях между n и k когда n>k или n=k. На рис. 1.10 представлен общий ход установления колебательного режима системы с сопротивлением при действии на нее гармонической возмущающей силы. Рисунок 1.10. Общий ход установления колебательного режима системы с сопротивлением при действии на нее гармонической возмущающей силы.
Из уравнения (1.16) можно сделать следующие выводы: а) Вынужденные колебания и при наличии сопротивлений происходят с частотой возмущающей силы. Это всеобщий закон вынужденных колебаний линейного осциллятора, имеющий место независимо от условий, в каких происходят его вынужденные колебания, в частности, независимо от того, имеются ли в системе сопротивления или нет. б) Амплитуда вынужденных колебаний от начальных условий и времени не зависит. С течением времени она не изменяется и, следовательно, вынужденные колебания, в отличие от свободных, от сопротивлений не затухают. При резонансе, когда p=k, амплитуда вынужденных колебаний остается конечной и притом не самой большой из возможных ее значений для данной системы. В самом деле, разыскивая значение р, при котором амплитуда
достигает максимума, найдем, что это случится, когда
т. е. до наступления резонанса, при p < k. в) В вынужденных колебаниях с сопротивлением всегда имеет место сдвиг фазы колебания по сравнению с фазой возмущающей силы. Величина ε этого сдвига определяется формулой
Максимальное значение, равное Амплитудой вынужденных колебаний определяются максимальные динамические напряжения, возникающие в упругих системах от воздействия на них гармонических возмущающих сил. В высшей степени важно заметить, что величина этих напряжений, как и амплитуды А, зависит не столько от величины возмущающей силы, сколько от частоты ее изменений во времени. При одном и том же значении H амплитуда и возникающие всистеме напряжения могут значительно изменяться в зависимости от изменений частоты р. Для оценки этих изменений их сравнивают со статическим отклонением A0 системы при действии на нее силы Н
Отношение амплитуды А к А0, равное
где
Эта кривая имеет разрыв в точке а =1. Рисунок 1.11. Ход изменения абсолютной величины коэффициента динамичности η Из рассмотрения резонансных кривых на рис. 1.11 обнаруживается следующий факт, имеющий значение в приближенных расчетах амплитуд вынужденных колебаний. В областях, достаточно далеких от резонанса, амплитуды при относительно малом сопротивлении почти не отличаются от соответствующих амплитуд вынужденных колебаний без сопротивления, определяемых более простой формулой
В этих областях при вычислении амплитуд можно совсем не учитывать сопротивлений, которые вообще с трудом поддаются точному определению. Хотя амплитуды вынужденных колебаний с сопротивлением остаются конечными и при резонансе, однако при более или менее продолжительной работе деталей машин в резонансных условиях всегда имеется опасность полного или частичного их разрушения от усталостных напряжений. Теперь стоит рассмотреть какие же нагрузки учитываются при расчете трубопроводов на динамическое нагружение и как они поределяются. Нагрузки и воздействия, вызывающие вибрацию трубопроводов, разделяются на группы: а) механические воздействия на трубопровод со стороны оборудования, вызванные неуравновешенностью движущихся масс, износом подшипников и т.д.; б) нестационарные гидравлические воздействия в результате: пульсации давления на входе в трубопровод от компрессора или насоса; прохождения по системе двухфазной среды, особенно в пробковом режиме, кавитации и т.п.; отрывных течений за местными сопротивлениями. Амплитуды возбуждающих вибрацию нагрузок и воздействий определяются расчетом или измерениями в процессе пуско-наладочных работ и задаются в виде перемещений или внешних сил. При оценке нестационарных гидродинамических воздействий рассматриваются те сечения трубопровода, где происходит изменение величины и направления скорости потока. Спектр частот пульсации, генерируемых поршневыми и центробежными машинами
где i = 1, 2, 3... ‑ номер гармоники, n - число оборотов вала в мин., m - число цилиндров поршневых или число лопаток центробежных нагнетательных машин. Если возбудителями пульсаций в трубопроводе являются местные гидравлические сопротивления, то генерируемая при этом частота рассчитывается по формуле
где V ‑ скорость потока, Для одиночных преград в формуле (17.3) принимается минимальное значение численного коэффициента, равное 200. При отсутствии местного сужения (прямая труба) численный коэффициент в (17.3) принимается равным 500. Для трубопроводов с двухфазным рабочим веществом учитывается возможность появления гидродинамических возмущений, особенно ощутимых в пробковом режиме. Амплитудно-частотные характеристики нестационарного воздействия двухфазного потока на местные сопротивления определяются при пуско-наладочных работах или предварительными расчетами. При проектировании учитывается возможность возникновения резонансных акустических колебаний при сближении значений генерируемых и собственных частот гидродинамических колебаний среды. Амплитудно-частотные характеристики акустических колебаний для сложных трубопроводных систем определяются расчетом или в процессе пуско-наладочных работ. Примечание. Собственную частоту акустических колебаний трубопровода для прямолинейных участков рекомендуется определять по формулам: для трубы с акустически открытыми или закрытыми концами:
для трубы с одним акустически открытым концом
где i = 1, 2, 3..., С ‑ скорость звука в м/с, L ‑ длина трубы в м.[21] При проектировании конструкции, подверженной воздействиям возмущающих сил, стараютсяпоэтому подобрать соотношения размеров и прочности ее деталей так, чтобы по возможности отодвинуть условия нормального режима работы ее от резонансных условий). Для той же цели служат специальные устройства, как, например, нелинейные муфты, виброгасители и т. п. Идея динамического виброгасителя основана на том, что если на колеблющуюся систему трубопровода установить дополнительную систему виброгасителя с собственной частотой, равной частоте возмущающей силы, то колебания грузов виброгасителя вызовут реакции, направленные в противоположную сторону, которые будут нейтрализовать внешнюю периодическую силу. Силы, разливаемые динамическим гасителем, определяются силами инерции, поэтому для более или менее полной нейтрализации возмущающей силы необходимо, чтобы гаситель обладал достаточно большой массой или большим ускорением, иначе говоря, большой амплитудой колебания.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 970; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ,
,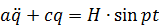
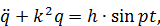 (1.10)
(1.10)

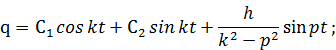
 . Тогда
. Тогда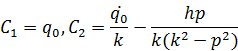
 (1.11)
(1.11) при t=0, такие колебания во все время действия возмущающей силы не возникают.
при t=0, такие колебания во все время действия возмущающей силы не возникают. (1.12)
(1.12)


 (1.13)
(1.13) в коэффициент которого входит множителем время t. Такой член называется вековым. С течением времени он растет по абсолютной величине безгранично, причем определяемые им колебания происходят с возрастающими по линейному закону отклонениями, как показано на рис. 1.9. Совпадение частоты возмущающей силы с собственной частотой системы и( сопровождающие его явления носят название резонанса.
в коэффициент которого входит множителем время t. Такой член называется вековым. С течением времени он растет по абсолютной величине безгранично, причем определяемые им колебания происходят с возрастающими по линейному закону отклонениями, как показано на рис. 1.9. Совпадение частоты возмущающей силы с собственной частотой системы и( сопровождающие его явления носят название резонанса.
 (1.13)
(1.13) (1.14)
(1.14)

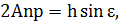

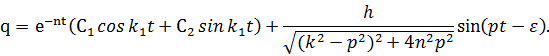

 (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17)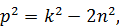
 (1.18)
(1.18) , сдвиг фазы имеет при резонансе, когда p=k.
, сдвиг фазы имеет при резонансе, когда p=k. (1.19)
(1.19) (1.20)
(1.20) называется коэффициентом динамичности. Коэффициент динамичности показывает во сколько раз максимальное динамическое отклонение при вынужденных колебаниях от силы H ∙ sin(pt) больше максимального статического отклонения от постоянной силы Н. На рис. 1.11, так называемыми, резонансными кривыми представлен ход изменения абсолютной величины коэффициента динамичности η в зависимости от частоты возмущающей силы
называется коэффициентом динамичности. Коэффициент динамичности показывает во сколько раз максимальное динамическое отклонение при вынужденных колебаниях от силы H ∙ sin(pt) больше максимального статического отклонения от постоянной силы Н. На рис. 1.11, так называемыми, резонансными кривыми представлен ход изменения абсолютной величины коэффициента динамичности η в зависимости от частоты возмущающей силы 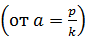 для некоторых значений коэффициента сопротивления
для некоторых значений коэффициента сопротивления  . Пунктиром показана резонансная кривая для n =0 в отсутствие сопротивления, когда коэффициент динамичности
. Пунктиром показана резонансная кривая для n =0 в отсутствие сопротивления, когда коэффициент динамичности (1.21)
(1.21) (1.22)
(1.22) ,
,
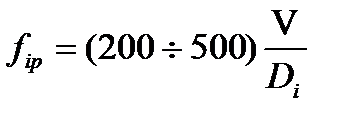 ,
,
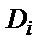 - диаметр сужения в местном сопротивлении.
- диаметр сужения в местном сопротивлении.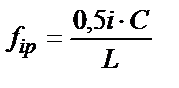 ,
,
 ,
,



